归并排序的C++实现

原创作品，转载请注明出处:点我

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

以上内容来自百度百科。

归并排序主要分为两部分：

1、划分子区间

2、合并子区间

现在以 9,6,7,22,20,33,16,20 为例讲解上面两个过程：

第一步，划分子区间：每次递归的从中间把数据划分为左区间和右区间。原始区间为[start,end],start=0,end=[length-1],减一是因为数组的下标从0开始,本例中length=8,end=7.现在从中间元素划分，划分之后的左右区间分别为 [start,(end-start+1)/2+start],右区间为[(end-start+1)/2+start+1,end],本例中把start和end带入可以得到[0,7]，划分后的左右子区间为[0,4],[5,7],然后分别对[start,end]=[0,4]和[start,end]=[5,7]重复上一步过程，直到每个子区间只有一个或者两个元素。整个分解过程为:

子区间划分好以后，分别对左右子区间进行排序，排好序之后，在递归的把左右子区间进行合并，整个过程如下图所示：

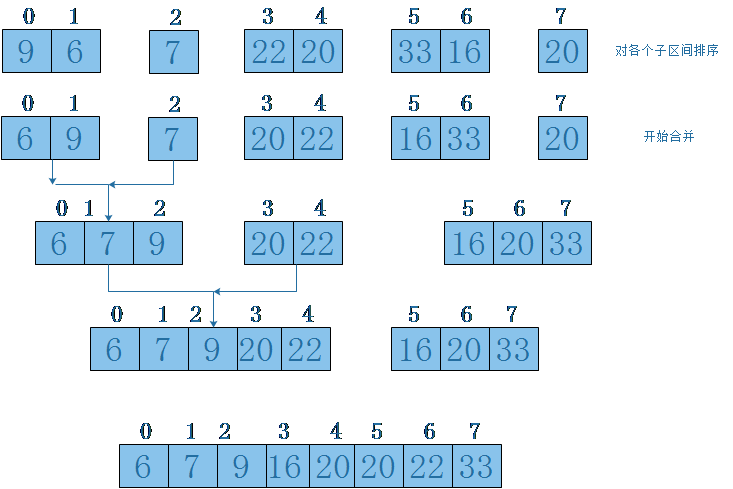
现在看代码：

 void merge_sort(int *data, int start, int end, int *result)
 {
     if( == end - start)//如果区间中只有两个元素，则对这两个元素进行排序
     {
         if(data[start] > data[end])
         {
             int temp  = data[start];
             data[start] = data[end];
             data[end] = temp;
         }
         return;
     }
     else if( == end - start)//如果只有一个元素，则不用排序
         return;
     else
     {
         //继续划分子区间，分别对左右子区间进行排序
         merge_sort(data,start,(end-start+)/+start,result);
         merge_sort(data,(end-start+)/+start+,end,result);
         //开始归并已经排好序的start到end之间的数据
         merge(data,start,end,result);
         //把排序后的区间数据复制到原始数据中去
         for(int i = start;i <= end;++i)
             data[i] = result[i];
     }
 }

merge的过程为：

 void merge(int *data,int start,int end,int *result)
 {
     int left_length = (end - start + ) /  + ;//左部分区间的数据元素的个数
     int left_index = start;
     int right_index = start + left_length;
     int result_index = start;
     while(left_index < start + left_length && right_index < end+)
     {
         //对分别已经排好序的左区间和右区间进行合并
         if(data[left_index] <= data[right_index])
             result[result_index++] = data[left_index++];
         else
             result[result_index++] = data[right_index++];
     }
     while(left_index < start + left_length)
         result[result_index++] = data[left_index++];
     while(right_index < end+)
         result[result_index++] = data[right_index++];
 }

现在对程序进行测试：

 int main()
 {
     int data[] = {,,,,,,,};
     const int length = ;
     int result[length];
     cout << "Before sorted:" << endl;
     for(int i = ;i < length;++i)
         cout << data[i] << "  ";
     cout << endl;
     cout << "After sorted:" << endl;
     merge_sort(data,,length-,result);
     for(int i = ;i < length;++i)
         cout << data[i] << "  ";
     cout << endl;

     return ;
 }

程序运行结果如下：