Match:Cyclic Nacklace(KMP的next数组的高级应用)(HDU 3746)

　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　串珠子

　　题目大意：给定一个字串，要你找到如果要使之成为循环串，在末尾需要的最小的字数（只能添加字符，不能删减字符）

　　首先联动一下之前做过的动态规划问题POJ 3280，当然了3280这一题是用的LD，因为他可以添加或者删除（加上修改也行，但是要改状态方程了）

　　而我们现在要讨论的这一题（HDU 3746）是有限制的，首先它只能添加不能删除，其次一定是要在末尾添加。

　　其实这样的题用kmp可以很快地解决，其实这样的题目是循环节的题目，之前我已经写过很多了，这一题是对循环节的深刻理解。

　　首先我们我们明白，对于kmp算法的next数组，如果一个字串是循环字串，那么他一定有len%(len-next[len])==0且next[len]>0，这个已经从1961等题论证了

　　现在我们就是要搞清楚，如果len%(len-next[len])!=0会如何，我们先来看一个例子

　　

　　比如上个例子，他的最大前缀和后缀是abcdeabcd，如果要在末尾加上字符使他循环，那么一定是要加上e，使新的循环节是abcde，而abcde的长度刚好是len-next[len]

　　

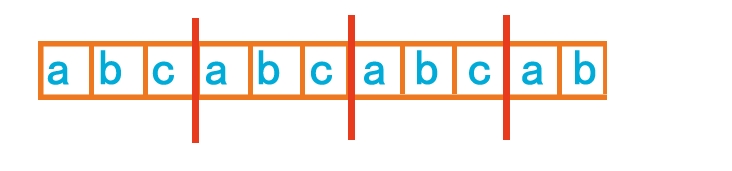
　　再如这个例子，最大前缀和后缀是abcabcab，末尾加上c循环节就是abc，刚好也是len-next[len]

　　

　　对于这个，不存在最大前后缀，必须加上len才能使之成为循环字串，而next[len]刚好是0，也符合len-next[len]

　　那么我们是不是能下结论，无论对于什么字串，无论是否循环，最小的循环节一定是len-next[len]呢？答案是最小循环节一定满足这个结论

　　我们再来看第二组

　　我们把最大前后缀对齐，发现突出的部分的长度就是新的数组的循环节的长度，事实上，我们将任何数组按照这个方式对齐都有这个结论，就是突出的长度刚好是新的数组的循环节的长度，而这个长度刚好就是len-next[len]（非严格证明），那么原数组按照新的循环节划分会剩下len%(len-next[len])个单元（注意len-next[len]要特判，因为可能会存在len-next[len]==0），接着我们就可以直接用len-len%(len-next[len])得到需要补齐的长度了，这就是循环节题目的一般做法。　　

　　参考：http://blog.csdn.net/u013480600/article/details/22954037

 #include <iostream>
 #include <algorithm>
 #include <functional>
 #include <string.h>

 using namespace std;

 static char input[];
 static int _Next[];

 void Get_Next(const int);

 int main(void)
 {
     int case_sum, len;
     scanf("%d", &case_sum);

     while (case_sum--)
     {
         scanf("%s", input);
         len = strlen(input);
         Get_Next(len);

         if (_Next[len] == )//不存在循环节
             printf("%d\n", len);
         else if (len % (len - _Next[len]) == )//已经是循环节了
             printf("0\n");
         else
             printf("%d\n", len - _Next[len] - len % (len - _Next[len]));
     }
     return EXIT_SUCCESS;
 }

 void Get_Next(const int len)
 {
     int i = , k = -;
     _Next[] = -;

     while (i < len)
     {
         if (k == - || input[i] == input[k])
         {
             i++;
             k++;
             _Next[i] = k;
         }
         else k = _Next[k];
     }
 }