ACM: Racing Gems - 最长递增序列

Racing Gems

 

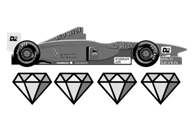
You are playing a racing game.  Your character starts at the x axis (y = 0) and proceeds up the      race track, which has a boundary at the line x = 0 and another at x = w.  You  may start the race       at any horizontal position you want, as long as it is within the track boundary.  The finish line is       at y = h, and the game ends when you reach that line.  You proceed at a fixed vertical velocity v,   but you can control your horizontal velocity to be any value between −v/r and v/r, and change it     at any time.

There are n gems at specific points on the race track.  Your  job is to collect as many gems as  possible.  How many gems can you collect?

Input

The first line of input contains four space-separated integers n, r, w, and h (1 ≤ n ≤ 105, 1 ≤ r ≤ 10,  1 ≤ w, h ≤ 109). Each of the following  n lines  contains  two  space-separated  integers  xi  and  yi, denoting the coordinate of the ith gem (0 ≤ xi ≤ w, 0 < yi ≤ h).  There will be at most one gem        per location.

The input does not include a value for    v.

Output

Print, on a single line, the maximum number of gems that can be collected during the  race.

Sample Input	Sample Output 3
5  1  10 10
8 8
5 1
4 6
4 7
7 9

Sample Input	Sample Output 3
5  1  100 100
27 75
79 77
40 93
62 41
52 45

Sample Input	Sample Output 4
10  3  30 30
14 9
2 20
3 23
15 19
13 5
17 24
6 16
21 5
14 10
3 6

/*/
题意，跑跑车游戏，x方向速度为1，y方向自己控制范围在-1/r到1/r之间。

给出金币的坐标，最多问能捡到多少金币。

首先可以知道，我们的可以走的范围为由出发点引出的左右两条射线之内，如果下一个点在现在的点的射线范围内，那么这个金币可以被捡到。

如果没有在射线范围内，就无法被捡到

上图

可以从图中看到下面第一个绿色的点A可以直接走到的点有两个 B 和C，但是B只能再走向E，而C可以走到D，再从D走到E；

明显A-C-D-E这种路径长些，想到这里，我们可以这样去解决这个问题：

把每个点的坐标按照左右位移的速度 1/r 映射到左右两个边界，按照左右两个边界升序排序【左边界优先】，取右边界最大上升子序列就行了。

这里用到了一个迭代器upper_bound(a,a+n,x)，它的作用是返回a数组中从x开始的递增序列的最后一个的地址。

AC代码：
/*/

#include"algorithm"
#include"iostream"
#include"cstring"
#include"cstdlib"
#include"cstdio"
#include"string"
#include"vector"
#include"queue"
#include"cmath"
using namespace std;
typedef long long LL ;
#define memset(x,y) memset(x,y,sizeof(x))
#define memcpy(x,y) memcpy(x,y,sizeof(x))
#define FK(x) cout<<"["<<x<<"]\n"
#define bigfor(x) for(LL qq=1;qq<= T ;qq++)

const LL MX=1e5+5;

struct Node {
	LL x,y;
	bool operator<(const Node &A)const {
		return x < A.x;
	}
	void add(LL r,LL w,LL xx,LL yy) {
		x=xx*r+yy;
		y=(w-xx)*r+yy;
	}
} nd[MX];

LL dp[MX];

int main() {
	LL n,r,w,h,x,y;
	while(~scanf("%I64d%I64d%I64d%I64d",&n,&r,&w,&h)) {
		for(LL i=1; i<=n; i++) {
			scanf("%I64d%I64d",&x,&y);
			nd[i].add(r,w,x,y);
		}
		LL ans=0;
		memset(dp,0x3f);
		sort(nd+1,nd+1+n);
		for(LL i=1; i<=n; i++) {
			LL tem=upper_bound(dp+1,dp+1+n,nd[i].y)-&dp[0];  //★
			ans = max(ans,tem);
			dp[tem]=nd[i].y;
		}
		printf("%I64d",ans);
	}
	return 0;
}

/*/
★升序排列的容器：
iterator lower_bound( const key_type &key ): 返回一个迭代器[地址]，指向键值>= key的第一个元素。
iterator upper_bound( const key_type &key ):返回一个迭代器[地址]，指向键值<=key的最后一个元素的后一个元素。
★降序排列的容器：
iterator lower_bound( const key_type &key ): 返回一个迭代器[地址]，指向键值<= key的第一个元素。
iterator upper_bound( const key_type &key ):返回一个迭代器[地址]，指向键值>=key的最后一个元素的后一个元素。
/*/