Note -「Variational Auto-Encoder」VAE 学习与 MNIST 实战

\(1\) 数学基础
- \(1.1\) KL 散度
- \(1.2\) Evidence Lower BOund (ELBO)
\(2\) 模型结构
\(3\) MNIST 实战
\(4\) 参考资料

\[\mathscr{Lorain~y~w~la~Lora~blea.}

\newcommand{\DS}[0]{\displaystyle}

% operators alias
\newcommand{\opn}[1]{\operatorname{#1}}
\newcommand{\card}[0]{\opn{card}}
\newcommand{\lcm}[0]{\opn{lcm}}
\newcommand{\char}[0]{\opn{char}}
\newcommand{\Char}[0]{\opn{Char}}
\newcommand{\Min}[0]{\opn{Min}}
\newcommand{\rank}[0]{\opn{rank}}
\newcommand{\Hom}[0]{\opn{Hom}}
\newcommand{\End}[0]{\opn{End}}
\newcommand{\im}[0]{\opn{im}}
\newcommand{\tr}[0]{\opn{tr}}
\newcommand{\diag}[0]{\opn{diag}}
\newcommand{\coker}[0]{\opn{coker}}
\newcommand{\id}[0]{\opn{id}}
\newcommand{\sgn}[0]{\opn{sgn}}
\newcommand{\Res}[0]{\opn{Res}}
\newcommand{\Ad}[0]{\opn{Ad}}
\newcommand{\ord}[0]{\opn{ord}}
\newcommand{\Stab}[0]{\opn{Stab}}
\newcommand{\conjeq}[0]{\sim_{\u{conj}}}
\newcommand{\cent}[0]{\u{\degree C}}
\newcommand{\Sym}[0]{\opn{Sym}}
\newcommand{\wg}[0]{\wedge}
\newcommand{\Wg}[0]{\bigwedge}

% symbols alias
\newcommand{\E}[0]{\exist}
\newcommand{\A}[0]{\forall}
\newcommand{\l}[0]{\left}
\newcommand{\r}[0]{\right}
\newcommand{\ox}[0]{\otimes}
\newcommand{\lra}[0]{\leftrightarrow}
\newcommand{\llra}[0]{\longleftrightarrow}
\newcommand{\iso}[1]{\overset{\sim}{#1}}
\newcommand{\eps}[0]{\varepsilon}
\newcommand{\Ra}[0]{\Rightarrow}
\newcommand{\Eq}[0]{\Leftrightarrow}
\newcommand{\d}[0]{\mathrm{d}}
\newcommand{\e}[0]{\mathrm{e}}
\newcommand{\i}[0]{\mathrm{i}}
\newcommand{\j}[0]{\mathrm{j}}
\newcommand{\k}[0]{\mathrm{k}}
\newcommand{\Ex}[0]{\mathbb{E}}
\newcommand{\D}[0]{\mathbb{D}}
\newcommand{\oo}[0]{\infty}
\newcommand{\tto}[0]{\rightrightarrows}
\newcommand{\mmap}[0]{\hookrightarrow}
\newcommand{\emap}[0]{\twoheadrightarrow}
\newcommand{\actl}[0]{\curvearrowright}
\newcommand{\actr}[0]{\curvearrowleft}
\newcommand{\nsubg}[0]{\triangleleft}
\newcommand{\nsupg}[0]{\triangleright}
\newcommand{\lin}[0]{\lim_{n\to\oo}}
\newcommand{\linf}[0]{\liminf_{n\to\oo}}
\newcommand{\lsup}[0]{\limsup_{n\to\oo}}
\newcommand{\ser}[0]{\sum_{n=1}^\oo}
\newcommand{\serz}[0]{\sum_{n=0}^\oo}
\newcommand{\isoto}[0]{\overset\sim\to}
\newcommand{\F}[0]{\mathbb F}
\newcommand{\x}[0]{\times}
\newcommand{\M}[0]{\mathbf{M}}
\newcommand{\T}[0]{\intercal}

% symbols with parameters
\newcommand{\der}[1]{\frac{\d}{\d #1}}
\newcommand{\ul}[1]{\underline{#1}}
\newcommand{\ol}[1]{\overline{#1}}
\newcommand{\wt}[1]{\widetilde{#1}}
\newcommand{\br}[1]{\l(#1\r)}
\newcommand{\bk}[1]{\l[#1\r]}
\newcommand{\ev}[1]{\l.#1\r|}
\newcommand{\abs}[1]{\l|#1\r|}
\newcommand{\bs}[1]{\boldsymbol{#1}}
\newcommand{\env}[2]{\begin{#1}#2\end{#1}} % why not?
\newcommand{\ALI}[1]{\env{aligned}{#1}}
\newcommand{\CAS}[1]{\env{cases}{#1}}
\newcommand{\pmat}[1]{\env{pmatrix}{#1}}
\newcommand{\dary}[2]{\l|\begin{array}{#1}#2\end{array}\r|}
\newcommand{\pary}[2]{\l(\begin{array}{#1}#2\end{array}\r)}
\newcommand{\pblk}[4]{\l(\begin{array}{c|c}{#1}&{#2}\\\hline{#3}&{#4}\end{array}\r)}
\newcommand{\u}[1]{\mathrm{#1}}
\newcommand{\lix}[1]{\lim_{x\to #1}}
\newcommand{\ops}[1]{#1\cdots #1}
\newcommand{\seq}[3]{{#1}_{#2}\ops,{#1}_{#3}}
\newcommand{\dedu}[2]{\u{(#1)}\Ra\u{(#2)}}

% SPECIAL
\newcommand{\dat}[1]{\bs{\mathrm{#1}}} % font for data point / data set
\]

限于笔者水平, 本文或仅适合 AEVB 及 VAE 的基础学习. 如果希望更深入地了解 VAE, 推荐阅读参考资料 \([1]\) 及相关文献.

对于数学水平要求, 本文仅假设读者掌握朴素概率论和入门的分析学.

\(1\) 数学基础

\(1.1\) KL 散度

The Kullback–Leibler divergence (also called relative entropy and I-divergence), denoted \(D_{\u{KL}}(P\parallel Q)\), is a type of statistical distance: a measure of how much a model probability distribution \(Q\) is different from a true probability distribution \(P\).

定量地, 离散条件下的 KL 散度定义为

\[\ALI{
D_{\u{KL}}(P\parallel Q) &:= \sum_{\dat x}P(\dat x)\log\frac{P(\dat x)}{Q(\dat x)}\\
&= -\sum_{\dat x}P(\dat x)\log Q(\dat x)+\sum_{\dat x}P(\dat x)\log P(\dat x).
}
\]

从信息熵 (也即 "相对熵" 这个名字) 的角度容易理解. 我们尝试用 \(Q\) 的最优编码方式 (即事件 \(\dat x\) 使用 \(-\log Q(\dat x)\) 个 bit 的编码) 来编码 \(P\), \(D_{\u{KL}}(P\parallel Q)\) 给出的就是这种编码所用 bit 数与直接最优编码 \(P\) 本身的 bit 数 (即 \(P\) 本身的熵) 的差值, 这一差值反应了把编码从 \(Q\) 直接迁移到 \(P\) 的 "某种代价". 在这样的直观理解下, 如果二者是同分布的, 这一差值显然是 \(0\); 而对于一般的 \(P\) 和 \(Q\), 也不难看出 \(D_{\u{KL}}(P\parallel Q)\ge 0\).

\(1.2\) Evidence Lower BOund (ELBO)

这里我们着重研究形如 \(D_{\u{KL}}(Q(\dat z)\parallel P(\dat z\mid\dat x))\) 的 KL 散度, 其中 \(\dat x\) 是某一特定事件, \(P(\dat z\mid\dat x)\) 给出此时 \(\dat z\) 的条件分布. 推导:

\[\ALI{
D_{\u{KL}}(Q\parallel P) &= \sum_{\dat z}Q(\dat z)\log\frac{Q(\dat z)P(\dat x)}{P(\dat x\dat z)} \\
&= \sum_{\dat z}Q(\dat z)\br{\log\frac{Q(\dat z)}{P(\dat x\dat z)}+\log P(\dat x)}\\
&= \sum_{\dat z}Q(\dat z)(\log Q(\dat z)-\log P(\dat x\dat z))+\underbrace{\sum_{\dat z}Q(\dat z)}_{=1}\log P(\dat x) \\
&= \sum_{\dat z}Q(\dat z)(\log Q(\dat z)-\log P(\dat x\dat z))+\log P(\dat x).
}
\]

对分布 \(Q(\dat z)\), 记 \(\Ex_Qf(\dat z):=\sum_{\dat z}Q(\dat z)f(\dat z)\), 则

\[D_{\u{KL}}(Q(\dat z)\parallel P(\dat z\mid\dat x))=\Ex_Q(\log Q(\dat z)-\log P(\dat x\dat z))+\log P(\dat x).
\]

\[\ALI{
\implies \log P(\dat x) &= D_{\u{KL}}(Q(\dat z)\parallel P(\dat z\mid\dat x))-\Ex_Q(\log Q(\dat z)-\log P(\dat x\dat z))\\
&=: D_{\u{KL}}(Q(\dat z)\parallel P(\dat z\mid\dat x))+\mathcal L(Q).
}\tag 1
\]

由于 \(D_{\u{KL}}(Q\parallel P)\ge 0\), 有

\[\log P(\dat X)\ge\mathcal L(Q).\tag 2
\]

即 \(\mathcal L(Q)\) 可以作为 \(\log P(\dat x)\) 的下界估计.

\(2\) 模型结构

\(2.1\) 基本假设

设数据集 \(\dat X=\{\dat x^{(i)}\}_{i=1}^N\) 由 \(N\) 个独立同分布的数据点构成. 我们假设它由以下过程采样而来:

从某个先验分布 \(p_{\dat\theta^*}(\dat z)\) 采样 \(\dat z^{(i)}\);
从某个条件分布 \(p_{\dat\theta^*}(\dat x\mid\dat z=\dat z^{(i)})\) 采样 \(\dat x^{(i)}\).

其中 \(p_{\dat\theta^*}(\dat z)\) 和 \(p_{\dat\theta^*}(\dat x\mid \dat z)\) 来自一族参数化分布 \(p_{\dat\theta}(\dat z)\) 和 \(p_{\dat\theta}(\dat x\mid\dat z)\), 且它们的概率密度函数对 \(\dat\theta\) 和 \(\dat z\) 几乎处处可微.

现在, 数据集 \(\dat X\) 是已知的, 但我们不知道隐变量 \(\dat z^{(i)}\) 和具体的分布参数 \(\dat\theta^*\). 因此, 我们尝试引入一个识别模型 \(q_{\dat\phi}(\dat z\mid \dat x)\) 用来估计真实的后验分布 \(p_{\dat\theta}(\dat z\mid\dat x)\), 并尝试一起学习 \(\dat\phi\) 和 \(\dat\theta\).

我们将在后验分布 \(p_{\dat\theta}(\dat z\mid\dat x)\) (\(q_{\dat\phi}(\dat z\mid\dat x)\)) 上采样 \(\dat z\) 的行为视作对数据 \(\dat x\) 的编码, 在条件分布 \(p_{\dat\theta}(\dat x\mid\dat z)\) 上采样 \(\dat x\) 的行为视作对编码 \(\dat z\) 的解码, 这就是所谓的 encode 和 decode 过程.

\(2.2\) Marginal Likelyhood

为了学到最优的 \(\dat\theta^*\), 我们势必需要引入一个评估分布参数优劣的值. 模仿最大似然的手法, 我们仍然研究数据集 \(\dat X\) 被模型生成的概率. 则对某个数据点 \(\dat x\) 和待评估的参数 \(\dat\theta\), 有

\[p_{\dat\theta}(\dat x)=\int p_{\dat\theta}(\dat x\mid\dat z)p_{\dat\theta}(z)\d z.
\]

(这里忽略了超参数 \(\alpha\). 为了让式子更完整, 可以在所有概率中 condition on \(\alpha\).) 而

\[\log p_{\dat\theta}(\dat X)=\sum_{i=1}^N\log p_{\dat\theta}(\dat x^{(i)}).
\]

利用识别模型 \(q_{\dat\phi}\) 估计后验分布, 套用 \((1)\), 我们知道

\[\log p_{\dat\theta}(\dat x^{(i)})=D_{\u{KL}}(q_{\dat\phi}(\dat z\mid\dat x^{(i)})\parallel p_{\dat\theta}(\dat z\mid\dat x^{(i)}))+\mathcal L(\dat\theta,\dat\phi;\dat x^{(i)}).
\]

同时由 \((2)\),

\[\ALI{
\log_{\dat\theta}(\dat x^{(i)}) &\ge \mathcal L(\dat\theta,\dat\phi;\dat x^{(i)})\\
&= \Ex_{q_{\dat\phi}(\dat z\mid \dat x^{(i)})}(-\log q_{\dat\phi}(\dat z\mid\dat x^{(i)})+\log p_{\dat\theta}(\dat x^{(i)}\dat z))&(3)\\
&= \Ex_{q_{\dat\phi}(\dat z\mid \dat x^{(i)})}(-\log q_{\dat\phi}(\dat z\mid\dat x^{(i)})+\log p_{\dat\theta}(\dat z)+\log p_{\dat\theta}(\dat x^{(i)}\mid\dat z))\\
&= -D_{\u{KL}}(q_{\dat\phi}(\dat z\mid \dat x^{(i)})\parallel p_{\dat \theta}(\dat z))+\Ex_{q_{\dat\phi}(\dat z\mid \dat x^{(i)})}(\log p_{\dat\theta}(\dat x^{(i)}\mid \dat z)).&(4)
}
\\
\]

我们希望通过对 \(\mathcal L(\dat\theta,\dat\phi;\dat x^{(i)})\) 梯度下降来学出优秀的 \(\dat\theta\) 和 \(\dat\phi\).

\(2.3\) 重参数化 (reparameterization) 与 AEVB 算法

然而 \([1]\) 中指出, \(\mathcal L(\dat\theta,\dat\phi;\dat x^{(i)})\) 对 \(\dat\phi\) 的梯度的方差很大, 不适用于数值计算. (不过对此论断, \([2]\) 的评论区中有不同的分析, 可自行了解.) 这里, 我们采用重参数化技巧: 对 \(\dat z\sim q_{\dat\phi}(\dat z\mid\dat x)\), 假定 \(\dat z=g_{\dat\phi}(\dat\epsilon,\dat x)\) 可微, \(\dat\phi\) 是参数, \(\dat\epsilon\sim p(\dat\epsilon)\) 是噪声. 以此为条件, 根据概率密度的定义:

\[q_{\dat\phi}(\dat z\mid\dat x)\d\dat z=p(\dat\epsilon)\d\dat\epsilon.
\]

进而

\[\ALI{
\Ex_{q_{\dat\phi}(\dat z\mid\dat x^{(i)})}f(\dat z) &= \int q_{\dat\phi}(\dat z\mid \dat x^{(i)})f(\dat z)\d\dat z\\
&= \int p(\dat\epsilon)f(g_{\dat\phi}(\dat\epsilon,\dat x^{(i)}))\d\dat\epsilon\\
&\approx \frac{1}{L}\sum_{\ell=1}^L f(\underbrace{g_{\dat\phi}(\dat\epsilon^{(\ell)},\dat x^{(i)})}_{=:\dat z^{(i,\ell)}}),\quad \dat\epsilon^{(\ell)}\sim p(\dat\epsilon).
}
\]

以此估计 \((3)\), 给出

\[\ALI{
\mathcal L(\dat\theta,\dat\phi;\dat x^{(i)}) &\approx \wt{\mathcal L}^A(\dat\theta,\dat\phi;\dat x^{(i)})\\
&:= \frac{1}{L}\sum_{\ell=1}^L(-\log q_{\dat\phi}(\dat z^{(i,\ell)}\mid\dat x^{(i)})+\log p_{\dat\theta}(\dat x^{(i)}\dat z^{(i,\ell)})).
}
\]

或者, 以此估计 \((4)\), 给出

\[\ALI{
\mathcal L(\dat\theta,\dat\phi;\dat x^{(i)}) &\approx \wt{\mathcal L}^B(\dat\theta,\dat\phi;\dat x^{(i)})\\
&:= -D_{\u{KL}}(q_{\dat\phi}(\dat z\mid\dat x^{(i)})\parallel p_{\dat\theta}(\dat z))+\frac{1}{L}\sum_{\ell=1}^L\log p_{\dat\theta}(\dat x^{(i)}\mid\dat z^{(i,\ell)}).
}
\]

前一项散度据 \([1]\) 称通常可以解析地求出.

接着, 在数据集 \(\dat X\) 上采样一个大小为 \(M\) 的 minibatch 来估计给定参数的 marginal likelyhood, 有

\[\ALI{
\mathcal L(\dat\theta,\dat\phi;\dat X) &\approx \wt{\mathcal L}^M(\dat\theta,\dat\phi;\dat X)\\
&:= \frac{N}{M}\sum_{i=1}^M\wt{L}(\dat\theta,\dat\phi;\dat x^{(i)}).
}
\]

(这里的 \(M\) 和单个数据点的采样数量 \(L\) 间可以 trade-off. \([1]\) 指出当 \(M=100\) 时 \(L=1\) 的表现已经出色.)

最终, 嵌套地使用 \(\wt{\mathcal L}^M\) 和 [\(\wt{\mathcal L}^A\) 或 \(\wt{\mathcal L}^B\)] 两次估计, 我们就能对 marginal likelyhood 的下界 ELBO 进行调优了. 这朴素地推导出 Auto-Encoding VB (AEVB) 算法:

\[\begin{array}{r|l}
& \text{Minibatch version of the Auto-Encoding VB algorithm}\\ \hline
0 & M,L\gets 100,1\\
1 & p(\dat\epsilon),p_{\dat\theta}(\dat x\mid\dat z),q_{\dat\phi}(\dat z\mid \dat x),p_{\dat\theta}(\dat z) \gets \text{chosen distri. forms}\\
2 & \dat\theta,\dat\varphi \gets \text{initial parameters}\\
3 & \textbf{repeat}\\
4 & \qquad \dat X^M \gets \text{minibatch sampled from }\dat X\\
5 & \qquad \dat \epsilon \gets \text{noise sampled from }p(\dat\epsilon)\\
6 & \qquad \dat g \gets \nabla_{\dat\theta,\dat\phi}\wt{\mathcal L}^M(\dat\theta,\dat\phi;\dat X^M,\dat\epsilon)\\
7 & \qquad \dat\theta,\dat\phi \gets \text{parameters optimized by }\dat g\\
8 & \textbf{until}~\text{convergence of }(\dat\theta,\dat\phi)\\
9 & \textbf{return}~\dat\theta,\dat\phi
\end{array}
\]

\(2.4\) 实例: VAE 算法

在 AEVB 的框架下, 不平凡的工作是指定分布 \(p(\dat\epsilon),p_{\dat\theta}(\dat x\mid\dat z),q_{\dat\phi}(\dat z\mid \dat x),p_{\dat\theta}(\dat z)\) 的形式. 在 Variational Auto-Encoder (VAE) 中, 我们取

\[\ALI{
p(\dat\epsilon) &= \mathcal N(\dat\epsilon;\bs 0,\bs 1),\\
q_{\dat\phi}(\dat z\mid\dat x^{(i)}) &= \mathcal N(\dat z;\dat\mu^{(i)},(\dat\sigma^2)^{(i)}\bs 1),\\
p_{\dat\theta}(\dat z) &= \mathcal N(\dat z;\bs 0,\bs 1),\\
g_{\dat\phi}(\dat\epsilon^{(\ell)},\dat x^{(i)}) &= \dat\mu^{(i)}+\dat\sigma^{(i)}\odot\dat\epsilon^{(\ell)}.
}
\]

其中 \(\bs 1\) 是适合尺寸的单位矩阵. \((\dat\sigma^2)^{(i)}\bs 1\) 给出的是对角协方差阵, 即每个 \(z_j\sim\mathcal N(\mu^{(i)}_j,(\sigma_j^{(i)})^2)\), 互相独立. (但个人感觉这个记号本身有些奇怪.)

而对于 \(p_{\dat\theta}(\dat x\mid\dat z)\), 可以根据数据类型选择:

对于二元数据, \(p_{\dat\theta}(x_i\mid\dat z)=\mathcal B(x_i;1,y_i)\), 其中 \(\dat y\) 由模型给出;
对于实值数据, \(p_{\dat\theta}(x_i\mid\dat z)=\mathcal N(x_i;\mu'_i,\sigma_i'^2)\), 其中 \(\dat\mu'\) 和 \(\dat\sigma'\) 由模型给出.

这里给出实值数据下 VAE 一次 encode-decode 的示意. 其中 \(\dat x\in\R^5\), \(\dat z\in\R^3\), 蓝色点云表示概率密度:

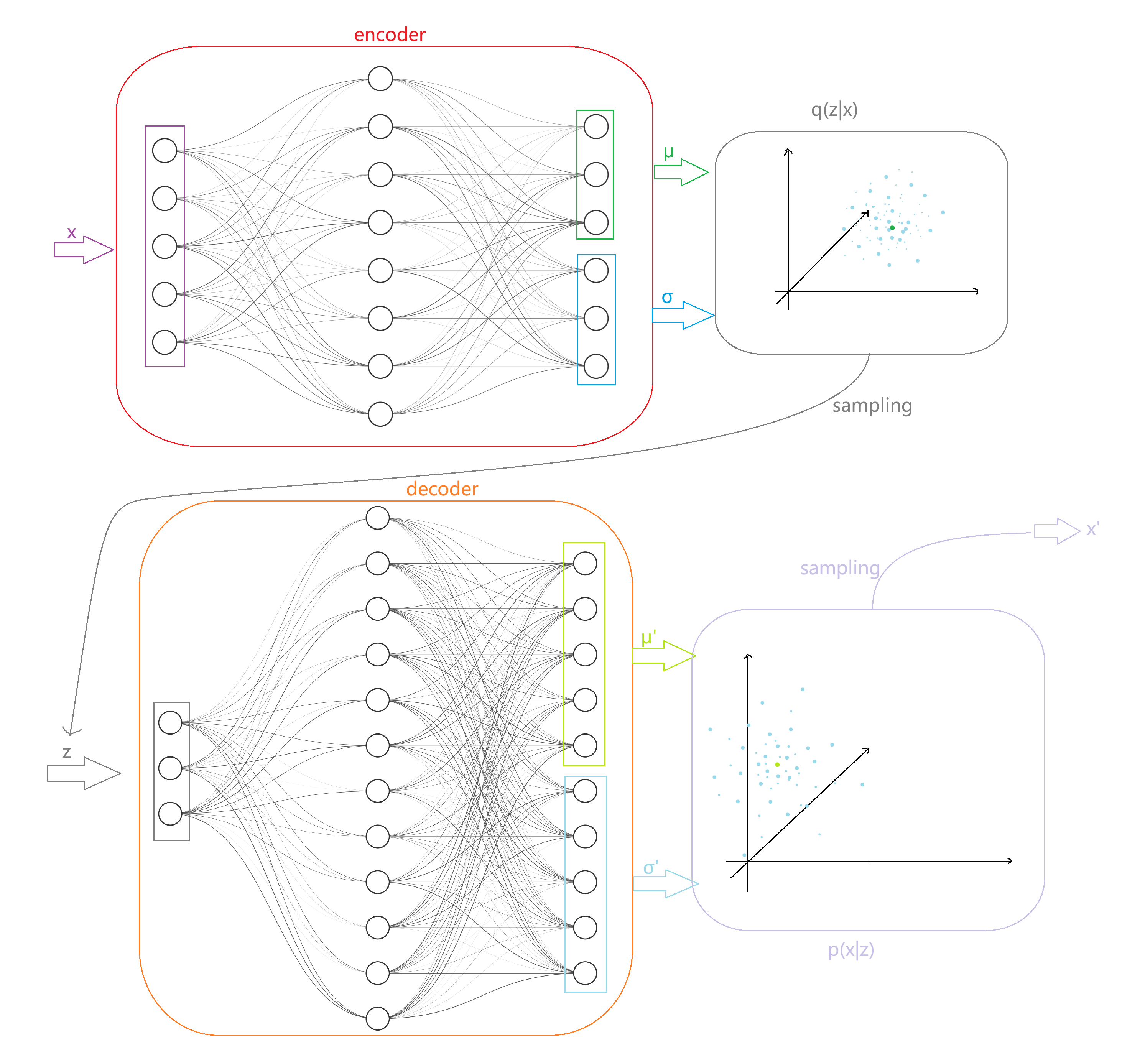
接下来还需要验证 \(\wt{\mathcal L}\) 的形式. 这里采用 \(\wt{\mathcal L}^B\) 的估计, 需要计算 \(-D_{\u{KL}}(q_{\dat\phi}(\dat z\mid\dat x^{(i)})\parallel p_{\dat\theta}(\dat z))+\frac{1}{L}\sum_{\ell=1}^L\log p_{\dat\theta}(\dat x^{(i)}\mid\dat z^{(i,\ell)})\). 对于前一项, \(q_{\dat\phi}(\dat z\mid\dat x^{(i)})\) 简记作 \(q_{\dat\phi}(\dat z)\), 设向量维度为 \(J\), 根据定义 (这里就是把离散情况的求和对应地变为分布函数上的 Lebesgue 积分, 我们在上文已经假设了这些分布良好的分析性质):

\[\ALI{
-D_{\u{KL}}(q_{\dat\phi}(\dat z)\parallel p_{\dat\theta}(\dat z)) &= \int q_{\dat\phi}(\dat z)\log p_{\dat\theta}(\dat z)\d\dat z-\int q_{\dat\phi}(\dat z)\log q_{\dat\phi}(\dat z)\d\dat z\\
&= \int\mathcal N(\dat z;\dat\mu,\dat\sigma^2)\log \mathcal N(\dat z;\bs 0,\bs 1)\d\dat z-\int\mathcal N(\dat z;\dat\mu,\dat\sigma^2)\log\mathcal N(\dat z;\dat\mu,\dat\sigma^2)\d\dat z\\
&=: I_1-I_2.
}
\]

容易计算:

\[\ALI{
I_1 &= \int\br{\prod_{j=1}^J\mathcal N(z_j;\mu_j,\sigma_j^2)}\sum_{j=1}^J\log \mathcal N(z_j;0,1)\d\dat z\\
&= \sum_{i=1}^J\int\mathcal N(z_i;\mu_i,\sigma_i^2)\log\mathcal N(z_i;0,1)\cdot\prod_{j\neq i}\mathcal N(z_j;\mu_j,\sigma_j^2)\d\dat z\\
&= \sum_{i=1}^J\int\mathcal N(z_i;\mu_i,\sigma_i^2)\log\mathcal N(z_i;0,1)\d z_i\cdot\underbrace{\prod_{j\neq i}\int\mathcal N(z_j;\mu_j,\sigma_j^2)\d z_j}_{=1}\\
&= -\frac{1}{2}\sum_{i=1}^J\int\frac{1}{\sqrt{2\pi}\sigma_i}\e^{-\frac{(z_i-\mu_i)^2}{2\sigma_i^2}}\br{\log(2\pi)+z_i^2}\d z_i\\
&= -\frac{1}{2}\sum_{i=1}^J\br{\log(2\pi)+\frac{1}{\sqrt{2\pi}\sigma_i}\int_{-\oo}^{+\oo}\e^{-\frac{x^2}{2\sigma_i^2}}(x^2+2\mu_ix+\mu_i^2)\d x}\\
&= -\frac{1}{2}\sum_{i=1}^J\br{\log(2\pi)+\mu_i^2+\frac{1}{\sqrt{2\pi}\sigma_i}\int_{-\oo}^{+\oo}x^2\e^{-\frac{x^2}{2\sigma_i^2}}\d x}
}
\]

回忆 Gauss 积分 \(\DS\int_{-\oo}^{+\oo}x^2\e^{-ax^2}\d x=\frac{1}{2}\sqrt{\frac{\pi}{a^3}}\), 代入化简得

\[\ALI{
I_1 &= -\frac{J}{2}\log(2\pi)-\frac{1}{2}\sum_{i=1}^J\br{\mu_i^2+\frac{1}{\sqrt{2\pi}\sigma_i}\cdot\frac{1}{2}\sqrt{8\sigma_i^6\pi}}\\
&= -\frac{J}{2}\log(2\pi)-\frac{1}{2}\sum_{i=1}^J(\mu_i^2+\sigma_i^2).
}
\]

同理

\[I_2=-\frac{J}{2}\log(2\pi)-\frac{1}{2}\sum_{i=1}^J(1+\log\sigma_j^2).
\]

所以

\[-D_{\u{KL}}(q_{\dat\phi}(\dat z)\parallel p_{\dat\theta}(\dat z))=\frac{1}{2}\sum_{i=1}^J(1+\log\sigma_i^2-\mu_i^2-\sigma_i^2).
\]

最终

\[\ALI{
\mathcal L(\dat\theta,\dat\phi;\dat x^{(i)}) &\approx \wt{\mathcal L}^B(\dat\theta,\dat\phi;\dat x^{(i)})\\
&= \frac{1}{2}\sum_{i=1}^J(1+\log\sigma_i^2-\mu_i^2-\sigma_i^2)+\frac{1}{L}\sum_{\ell=1}^L\log p_{\dat\theta}(\dat x^{(i)}\mid \dat z^{(i,\ell)}).
}
\]

这样的良好形式已然可以启动训练了. 在这一表达式中, 前一项即 (负) KL 散度, 后一项一般称为重构损失 (reconstruction loss).

\(3\) MNIST 实战

由于 VAE 和最常见的 "将 batch 输入模型 - 比对模型输出与 ground truth 计算 loss - 反向传播" 的训练方式有些差异, 实现起来可能有些难度. 所以这里以 MNIST 为例实现完整的 VAE, 并通过一些数据实验加深对 VAE 的理解.

(注: 文末提供了本节的完整代码.)

\(3.1\) 数据准备

无需多言. (Tips: MNIST 单图的初始形态为 \((1,28,28)\); ToTensor() 后灰度值在 \([0,1]\) 中.)

import torch

import torch.nn as nn

import torch.nn.functional as F

import torchvision

import matplotlib

matplotlib.use("Agg") # 笔者使用的 WSL

import matplotlib.pyplot as plt

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

train_dataset = torchvision.datasets.MNIST(root='./data', train=True, download=True)

train_dataset.transform = torchvision.transforms.ToTensor()

# 注意这里的 100 对应了训练量时 M 的值

train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=100, shuffle=True)

\(3.2\) 分布选取与框架代码

实践上, 在 decode 时直接采用独立 Bernoulli 分布是一个高质且高效的选择. 这时

\[\log p_{\dat\theta}(\dat x^{(i)}\mid\dat z^{(i,\ell)})=\sum_{j}\br{x^{(i)}_j\log\mu'_j+(1-x^{(i)}_j)\log(1-\mu'_j)},
\]

其中 \(\dat \mu'=\dat \mu'(\dat z^{(i,\ell)})\) 即 decode 样本点 \(\dat z^{(i,\ell)}\) 的模型输出 (不必再如上文图中输出一个 \(\dat\sigma'\)).

Q1: 灰度值是一个实值量, 为什么不如上文所说地使用正态分布来 decode?

A1: 用正态分布的最大问题是范围不匹配. 正态分布会给出 \(\R\) 上的采样, 如果不在训练过程中强制截断, 会导致重构损失非常巨大 (实测 \(10^9\) 倍于 KL 散度) 而难以训练; 而强制截断则会导致边界概率密度的不合理分配.

Q2: 图像灰度值分布的 ground truth 总该是 \([0,1]\) 上的连续分布, 我们用离散的 Bernoulli 分布去拟合合理吗?

A2: 的确, Bernoulli 分布无法建模中间灰度, 理论上有偏差. 如果希望更精确地拟合, 可以采用独立 Beta 分布等分布模型. Bernoulli 分布的优势在于其模型简单, 训练高效且稳定.

给出框架代码:

class Encoder(nn.Module):

    def __init__(self, LATENT_DIM):

        super(Encoder, self).__init__()

        self.W_h = nn.Linear(784, 256)

        self.b_h = nn.Parameter(torch.zeros(256))

        self.W_mu = nn.Linear(256, LATENT_DIM)

        self.b_mu = nn.Parameter(torch.zeros(LATENT_DIM))

        self.W_sgm = nn.Linear(256, LATENT_DIM)

        self.b_sgm = nn.Parameter(torch.zeros(LATENT_DIM))

    def forward(self, x):

        x = x.view((-1, 784))

        h = F.relu(self.W_h(x) + self.b_h) # 也可以用 tanh 等激活

        mu = self.W_mu(h) + self.b_mu

        sgm = self.W_sgm(h) + self.b_sgm # sigma 可能 <0, 其行为和 >0 一致

        return mu, sgm

class Decoder(nn.Module):

    def __init__(self, LATENT_DIM):

        super(Decoder, self).__init__()

        self.W_h = nn.Linear(LATENT_DIM, 256)

        self.b_h = nn.Parameter(torch.zeros(256))

        self.W_mu = nn.Linear(256, 784)

        self.b_mu = nn.Parameter(torch.zeros(784))

    def forward(self, z):

        h = F.relu(self.W_h(z) + self.b_h)

        mu_re = F.sigmoid(self.W_mu(h) + self.b_mu)

        return mu_re # 使用 Bernoulli 分布, 只输出 mu'

class VAE(nn.Module):

    def __init__(self, LATENT_DIM):

        super(VAE, self).__init__()

        self.LATENT_DIM = LATENT_DIM

        self.encoder = Encoder(LATENT_DIM)

        self.decoder = Decoder(LATENT_DIM)

    def generate(self, num=1): # [用于测试] 在隐空间随机采样重构

        imgs = None

        with torch.no_grad():

            z = torch.randn((num, self.LATENT_DIM)).to(device)

            mu_re = self.decoder(z)

            imgs = mu_re.view(-1, 1, 28, 28)

        return imgs.cpu()

    def reconstruct(self, X): # [用于测试] 模拟 encode-decode (如上文图过程)

        mu, sgm = self.encoder(X)

        eps = torch.randn_like(sgm).to(device)

        z = mu + sgm * eps

        mu_re = self.decoder(z)

        return mu_re.view(-1, 1, 28, 28).cpu()

    # 没有必要实现 forward 方法

class ELBO_Estimator(nn.Module):

    def __init__(self):

        super(ELBO_Estimator, self).__init__()

        self.L = 1 # 估算积分时的采样次数

        self.FIX_EPS = 1e-8 # /0, log0 修正

    def forward(self, X_M):

        mu, sgm = model.encoder(X_M)

        kl_div = -0.5 * torch.sum(1 + torch.log(sgm**2 + self.FIX_EPS) - mu**2 - sgm**2)

        re_loss = 0

        for _ in range(self.L):

            e_l = torch.randn_like(sgm).to(device) # 批量采样 epsilon

            z_l = mu + sgm * e_l

            mu_re = model.decoder(z_l)

            re_loss += torch.sum(X_M * torch.log(mu_re + self.FIX_EPS))

            re_loss += torch.sum((1 - X_M) * torch.log(1 - mu_re + self.FIX_EPS))

        re_loss /= self.L

        elbo = -(re_loss - kl_div)  # 负的 ELBO (调优时最小化之), 忽略了常数因子

        return elbo, kl_div, re_loss # 后两项用于输出时观察

\(3.3\) 训练

无需多言.

model = VAE(2).to(device) # 这里 2 是隐空间维度, 可以自由调节

criterion = ELBO_Estimator().to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=1e-3) # 随手写的学习率

def train_vae(model, train_loader, optimizer, epochs=10):

    model.train()

    for epoch in range(epochs):

        total_loss = 0

        for batch_idx, (data, _) in enumerate(train_loader):

            data = data.view((-1, 784)).float().to(device)

            optimizer.zero_grad()

            loss, kl_div, re_loss = criterion(data) # 直接算 criterion, 不必 model.forward

            loss.backward()

            optimizer.step()

            total_loss += loss.item()

            if batch_idx % 100 == 0:

                print(f'batch {batch_idx + 1}/{len(train_loader)} | loss: {loss.item():.2f}',

                      f'| kl_div: {kl_div.item():.2f} | re_loss: {re_loss.item():.2f}')

        print(f'---epoch {epoch + 1}/{epochs} | loss: {total_loss / len(train_loader):.2f}---\n')

# 启动训练

train_vae(model, train_loader, optimizer, epochs=10)

torch.save(model.state_dict(), f'vae.pth')

\(3.4\) 实验

先来观察直接在整个隐空间采样 \(\dat z\) 并重构的效果.

def generate_grid(model):

    model.eval()

    with torch.no_grad():

        imgs = model.generate(16)

        grid = torchvision.utils.make_grid(imgs, nrow=4, padding=2)

        plt.figure(figsize=(10, 10))

        plt.imshow(grid.permute(1, 2, 0).squeeze(), cmap='gray')

        plt.axis('off')

        plt.savefig('grid.png', format='png')

        plt.close()

generate_grid(model)

结果 (LATENT_DIM=10):

每个 "数字" 看上去是若干个标准数字的模糊叠加. 直接这样生成数字虽然勉强能看, 但的确不够理想.

接着再来对比 encode-decode 过程下的原数据 \(\dat x\) 和还原数据 \(\dat x'\).

def reconstruct_compare(model, valid_loader):

    model.eval()

    with torch.no_grad():

        for data, _ in valid_loader:

            data = data.view((-1, 784)).float().to(device)

            recons = model.reconstruct(data)

            data = data.view(-1, 1, 28, 28).cpu()

            # 制作 data 和 recons 的对比网格图

            grid = torchvision.utils.make_grid(torch.cat((data.view(-1, 1, 28, 28),

                                                          recons), dim=0), nrow=8, padding=2)

            plt.figure(figsize=(10, 10))

            plt.imshow(grid.permute(1, 2, 0).squeeze(), cmap='gray')

            plt.axis('off')

            plt.savefig('compare.png', format='png')

            plt.close()

            break

valid_dataset = torchvision.datasets.MNIST(root='./data', train=False, download=True)

valid_dataset.transform = torchvision.transforms.ToTensor()

valid_loader = torch.utils.data.DataLoader(valid_dataset, batch_size=16, shuffle=False)

reconstruct_compare(model, valid_loader)

结果 (LATENT_DIM=10):

效果不错. 像 \(1,0,7\) 这几个不太容易混淆的数字, 还原的数字看上去甚至更圆润美观一些. 但左起第一列的 \(5\), 倒数第二列的 \(4\) 和最后一列的 \(9\) 的还原得效果较差, 这可能是因为原数据就不太容易分辨.

最后, 我们取 LATENT_DIM=2 并观察隐空间形态. 这里我们取验证集全体进行 encode, 并描出每个点的正态中心:

def show_2d_latent_space(model, valid_loader, no_offset=False):

    model.eval()

    assert model.LATENT_DIM == 2, "Latent dimension must be 2 for visualization"

    with torch.no_grad():

        all_z = []

        all_labels = []

        for data, labels in valid_loader:

            data = data.view((-1, 784)).float().to(device)

            mu, sgm = model.encoder(data)

            if no_offset:

                z = mu

            else:

                eps = torch.randn_like(sgm).to(device)

                z = mu + sgm * eps

            all_z.append(z.cpu())

            all_labels.append(labels.cpu())

        all_z = torch.cat(all_z, dim=0)

        all_labels = torch.cat(all_labels, dim=0)

        plt.figure(figsize=(12, 12))

        scatter = plt.scatter(all_z[:, 0], all_z[:, 1], c=all_labels, cmap='tab10', alpha=0.5)

        plt.colorbar(scatter)

        plt.title('2D Latent Space')

        plt.xlabel('Latent Dimension 1')

        plt.ylabel('Latent Dimension 2')

        plt.savefig('latent-space.png', format='png')

        plt.close()

show_2d_latent_space(model, valid_loader, no_offset=True)

结果:

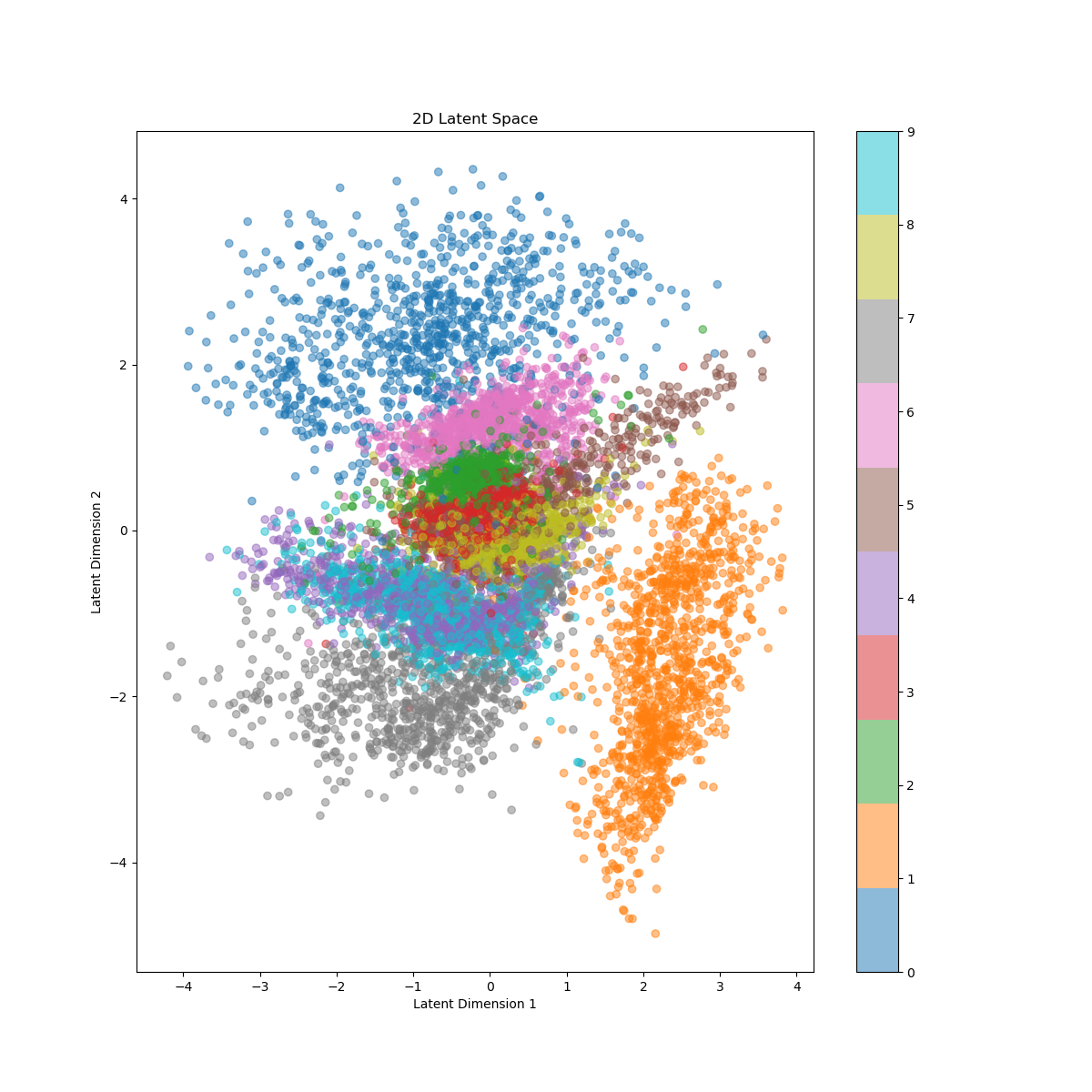
我们难以解释隐空间坐标轴的意义. 从散点来观察, 十个数字大致存在各自聚类的趋势. \(1,0,7\) 与其他数字的距离较远, 这和刚刚的还原效果以及我们区分数字的直观感受相合. 图上看最难区分的事 \(4\) 和 \(9\), 从形态上看可以理解, 且依照笔者在 MNIST 上测试的经验, 很多分辨 \(4\) 和 \(9\) 的任务的确是强人 (指人类) 所难, 所以也模型在此的模糊性也值得原谅.

另外, 在重复试验时, 空间一般会发生一些典范的变化: 例如上下左右翻转, 坐标轴交换等. 但散点的总体形态却总是类似.

\(4\) 参考资料

\([1]\) Kingma, Diederik P., and Max Welling. "Auto-encoding variational bayes." 20 Dec. 2013;

\([2]\) 知乎专栏: 变分自编码器 (VAEs), Gapeng, 2017-11-07 00:28;

\([3]\) 维基百科: Marginal likelihood, 21 February 2025, at 00:14 (UTC);

\([4]\) 维基百科: Kullback–Leibler divergence, 5 July 2025, at 21:27 (UTC).

附完整代码

import torch

import torch.nn as nn

import torch.nn.functional as F

import torchvision

import matplotlib

matplotlib.use("Agg")

import matplotlib.pyplot as plt

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

train_dataset = torchvision.datasets.MNIST(root='./data', train=True, download=True)

train_dataset.transform = torchvision.transforms.ToTensor()

train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=100, shuffle=True)

class Encoder(nn.Module):

    def __init__(self, LATENT_DIM):

        super(Encoder, self).__init__()

        self.W_h = nn.Linear(784, 256)

        self.b_h = nn.Parameter(torch.zeros(256))

        self.W_mu = nn.Linear(256, LATENT_DIM)

        self.b_mu = nn.Parameter(torch.zeros(LATENT_DIM))

        self.W_sgm = nn.Linear(256, LATENT_DIM)

        self.b_sgm = nn.Parameter(torch.zeros(LATENT_DIM))

    def forward(self, x):

        x = x.view((-1, 784))

        h = F.relu(self.W_h(x) + self.b_h)

        mu = self.W_mu(h) + self.b_mu

        sgm = self.W_sgm(h) + self.b_sgm

        return mu, sgm

class Decoder(nn.Module):

    def __init__(self, LATENT_DIM):

        super(Decoder, self).__init__()

        self.W_h = nn.Linear(LATENT_DIM, 256)

        self.b_h = nn.Parameter(torch.zeros(256))

        self.W_mu = nn.Linear(256, 784)

        self.b_mu = nn.Parameter(torch.zeros(784))

    def forward(self, z):

        h = F.relu(self.W_h(z) + self.b_h)

        mu_re = F.sigmoid(self.W_mu(h) + self.b_mu)

        return mu_re

class VAE(nn.Module):

    def __init__(self, LATENT_DIM):

        super(VAE, self).__init__()

        self.LATENT_DIM = LATENT_DIM

        self.encoder = Encoder(LATENT_DIM)

        self.decoder = Decoder(LATENT_DIM)

    def generate(self, num=1):

        imgs = None

        with torch.no_grad():

            z = torch.randn((num, self.LATENT_DIM)).to(device)

            mu_re = self.decoder(z)

            imgs = mu_re.view(-1, 1, 28, 28)

        return imgs.cpu()

    def reconstruct(self, X):

        mu, sgm = self.encoder(X)

        eps = torch.randn_like(sgm).to(device)

        z = mu + sgm * eps

        mu_re = self.decoder(z)

        return mu_re.view(-1, 1, 28, 28).cpu()

class ELBO_Estimator(nn.Module):

    def __init__(self):

        super(ELBO_Estimator, self).__init__()

        self.L = 1

        self.FIX_EPS = 1e-8

    def forward(self, X_M):

        mu, sgm = model.encoder(X_M)

        kl_div = -0.5 * torch.sum(1 + torch.log(sgm**2 + self.FIX_EPS) - mu**2 - sgm**2)

        re_loss = 0

        for _ in range(self.L):  # sampling integral ranges

            e_l = torch.randn_like(sgm).to(device)

            z_l = mu + sgm * e_l

            mu_re = model.decoder(z_l)

            re_loss += torch.sum(X_M * torch.log(mu_re + self.FIX_EPS))

            re_loss += torch.sum((1 - X_M) * torch.log(1 - mu_re + self.FIX_EPS))

        re_loss /= self.L

        elbo = -(re_loss - kl_div)  # negated ELBO, constant factors ignored

        return elbo, kl_div, re_loss

model = VAE(2).to(device)

criterion = ELBO_Estimator().to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

def train_vae(model, train_loader, optimizer, epochs=10):

    model.train()

    for epoch in range(epochs):

        total_loss = 0

        for batch_idx, (data, _) in enumerate(train_loader):

            data = data.view((-1, 784)).float().to(device)

            optimizer.zero_grad()

            loss, kl_div, re_loss = criterion(data)

            loss.backward()

            optimizer.step()

            total_loss += loss.item()

            if batch_idx % 100 == 0:

                print(f'batch {batch_idx + 1}/{len(train_loader)} | loss: {loss.item():.2f}',

                      f'| kl_div: {kl_div.item():.2f} | re_loss: {re_loss.item():.2f}')

        print(f'---epoch {epoch + 1}/{epochs} | loss: {total_loss / len(train_loader):.2f}---\n')

def generate_grid(model):

    model.eval()

    with torch.no_grad():

        imgs = model.generate(16)

        grid = torchvision.utils.make_grid(imgs, nrow=4, padding=2)

        plt.figure(figsize=(10, 10))

        plt.imshow(grid.permute(1, 2, 0).squeeze(), cmap='gray')

        plt.axis('off')

        plt.savefig('grid.png', format='png')

        plt.close()

def reconstruct_compare(model, valid_loader):

    model.eval()

    with torch.no_grad():

        for data, _ in valid_loader:

            data = data.view((-1, 784)).float().to(device)

            recons = model.reconstruct(data)

            data = data.view(-1, 1, 28, 28).cpu()

            # 制作 data 和 recons 的对比网格图

            grid = torchvision.utils.make_grid(torch.cat((data.view(-1, 1, 28, 28),

                                                          recons), dim=0), nrow=8, padding=2)

            plt.figure(figsize=(10, 10))

            plt.imshow(grid.permute(1, 2, 0).squeeze(), cmap='gray')

            plt.axis('off')

            plt.savefig('compare.png', format='png')

            plt.close()

            break

def show_2d_latent_space(model, valid_loader, no_offset=False):

    model.eval()

    assert model.LATENT_DIM == 2, "Latent dimension must be 2 for visualization"

    with torch.no_grad():

        all_z = []

        all_labels = []

        for data, labels in valid_loader:

            data = data.view((-1, 784)).float().to(device)

            mu, sgm = model.encoder(data)

            if no_offset:

                z = mu

            else:

                eps = torch.randn_like(sgm).to(device)

                z = mu + sgm * eps

            all_z.append(z.cpu())

            all_labels.append(labels.cpu())

        all_z = torch.cat(all_z, dim=0)

        all_labels = torch.cat(all_labels, dim=0)

        plt.figure(figsize=(12, 12))

        scatter = plt.scatter(all_z[:, 0], all_z[:, 1], c=all_labels, cmap='tab10', alpha=0.5)

        plt.colorbar(scatter)

        plt.title('2D Latent Space')

        plt.xlabel('Latent Dimension 1')

        plt.ylabel('Latent Dimension 2')

        plt.savefig('latent-space.png', format='png')

        plt.close()

# train_vae(model, train_loader, optimizer, epochs=10)

# torch.save(model.state_dict(), f'vae.pth')

valid_dataset = torchvision.datasets.MNIST(root='./data', train=False, download=True)

valid_dataset.transform = torchvision.transforms.ToTensor()

valid_loader = torch.utils.data.DataLoader(valid_dataset, batch_size=16, shuffle=False)

model.load_state_dict(torch.load(f'vae.pth'))

# generate_grid(model)

# reconstruct_compare(model, valid_loader)

show_2d_latent_space(model, valid_loader, no_offset=True)