学习笔记/DP：wqs 二分概述

1. 概述

1.0. 概述

wqs 二分，即王钦石二分，是一种通过降维来优化 dp 的处理手段。在 OI 中，wqs 二分最常用于处理一类 2D/1D dp，常搭配斜率优化、决策单调性等其他 dp 优化方式使用，较为套路。

1.1. 适用题型

wqs 二分处理的题型: 选取若干个（组）物品，数量有限制，选取有代价，询问代价极值。

$\text{eg.}$ 给定一数列 $a_n$，要求将其按顺序分割为 $c$ 组，使得每组的代价和最小，其中每组的代价定义为该组内所有数的和的平方。$n,c\le10^5,a_i\ge1$。

显然有 2D/1D 的 dp：设 $f_{i,j}$ 为前 $i$ 个数分了 $j$ 组的方案，答案即为 $f_{n,c}$，转移显然，预处理前缀和并滚掉第二维，时间复杂度 $\mathcal{O}(cn^2)$。斜率优化可做到 $\mathcal{O}(cn)$，但依旧无法通过。

实际上，这大部分这一类型的题目都有类似的 2D/1D dp 的做法。

1.2. 使用前提与凸性证明

能使用 wqs 二分的前提: 记 $f(i)$ 为选取 $i$ 个物品时的答案，$f$ 是凸函数，且可快速计算极值和极值点。

证明函数的凸性方法很多，可以结合题目感性猜测其凸性，或是打表进行观察。

更多严谨的凸性证明见 OI Wiki，反正我看不懂 qaq。

2. 第一种理解

2.0. 核心思想

在讲算法之前，先给出它的核心思想：

令我们想求的值为 $f(c)$，我们通过对 $f$ 的解析式的处理形成一个新的函数 $g$，使得新的函数 $g$ 仍可快速计算极值和极值点，且其极值点恰为 $(c,g(c))$，再利用 $f$ 和 $g$ 的关系反推 $f(c)$。

听着很神奇，但先记好这个核心思想。

2.1. 算法流程

我们开始了，首先画出 $f$ 的图像，显然它是一个离散的凸壳，接下来我们均考虑 $f$ 下凸的情况：

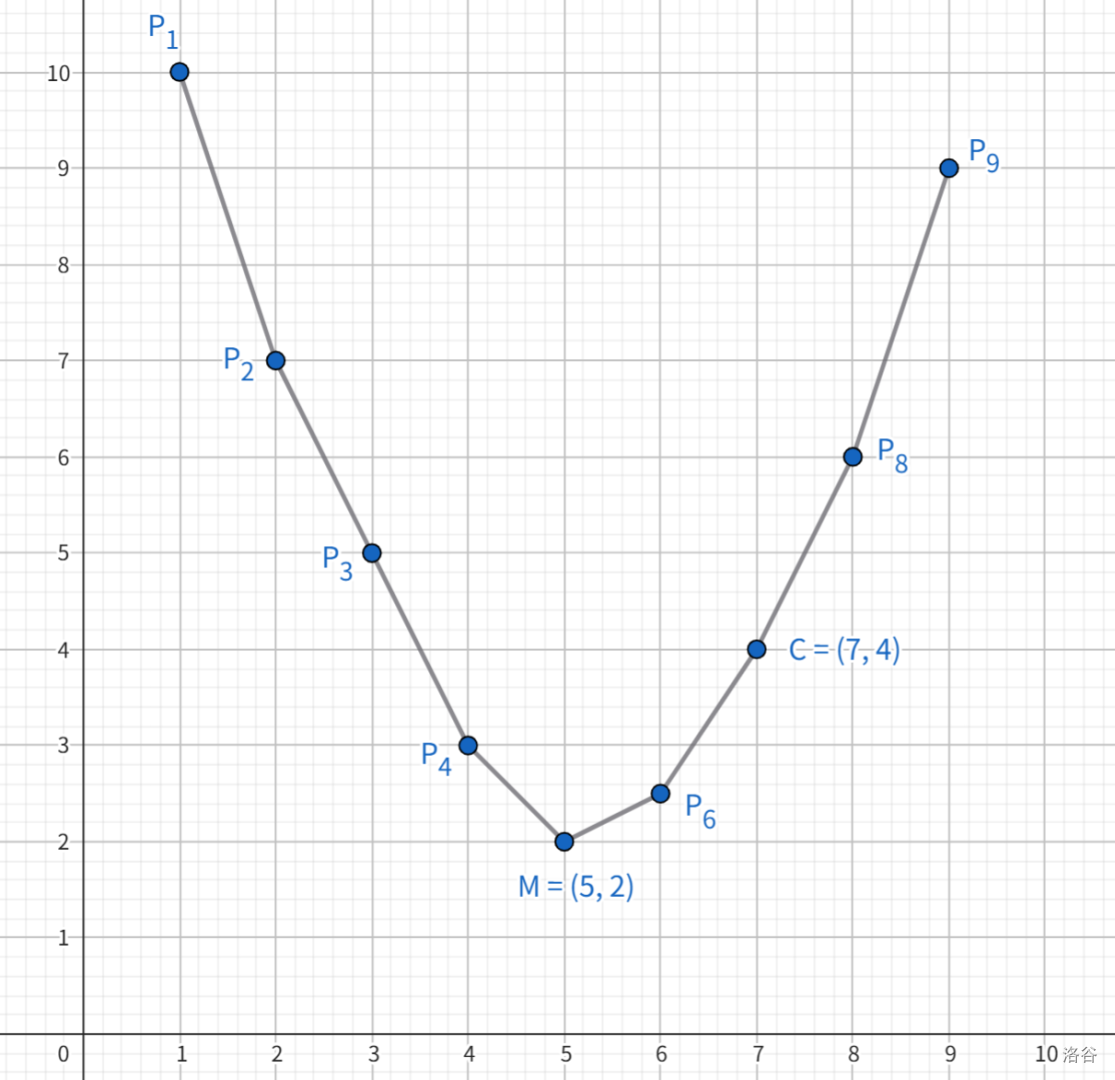
此时我们要求可以快速求出其最小值点，记此时的最小值点为 $m$。如图，画出 $f$ 的导函数图像 $f'$，$(m,f'(m))$ 与 $(m+1,f'(m+1))$ 的连线与 $x$ 轴有交）。$f$ 下凸，$f'$ 是增函数。

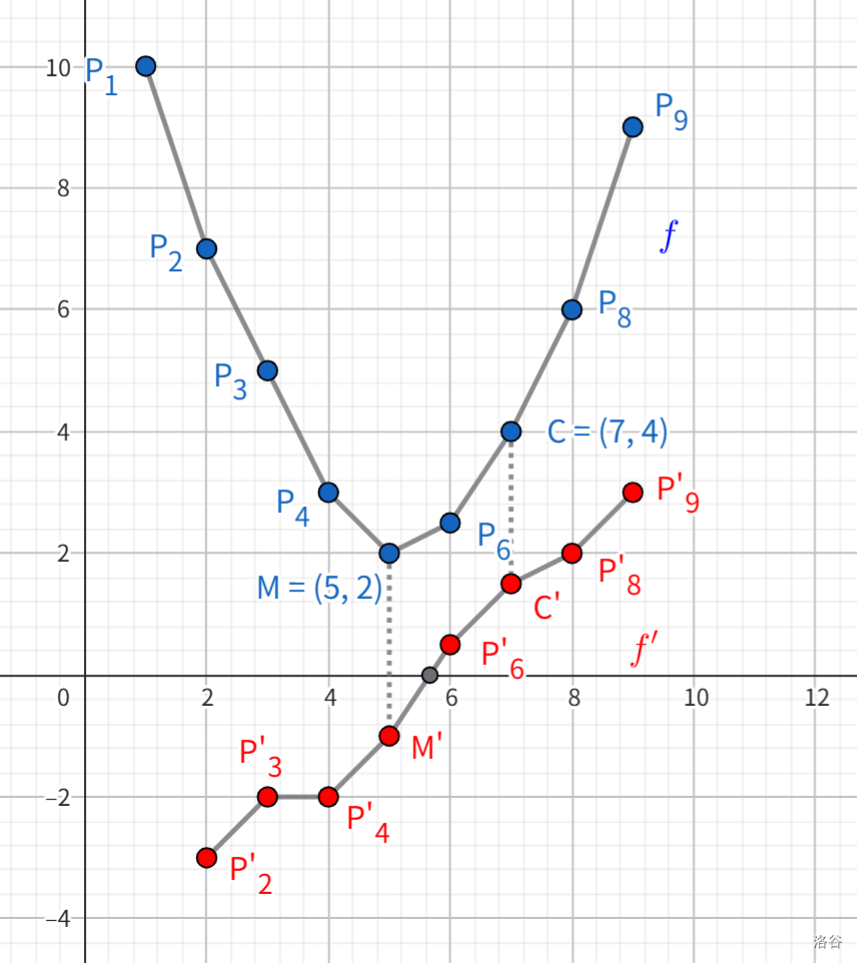
补充说明:

凸壳哪来的导数？

类比导数的定义，我们此处导数均指差分，即 $f'(i)=\Delta_{i}=f(i)-f(i-1)$，那么此时取到最小值的点的差分为正，且它下一个数的差分为正，自己画图理解一下。但不管怎么样，肯定可以通过平移使得 $g'(c)=0$。二分的时候，由于我们是 dp 求极值和极值点的，所以无关紧要。

依照概述部分的核心思想，我们考虑如何构造这个 $g$：首先我们希望最小值点落在 $c$，怎么办呢？我们从 $g'$ 入手。若希望最小值点落在 $c$，需要 $(c,g'(c))$ 与 $(c+1,f'(c+1))$ 的连线与 $x$ 轴有交，不妨令 $g'(c)=0$。我们让 $f'$ 的图像在垂直方向上运动，由于它是增函数，感性理解，我们总能让它的零点落到 $c$ 上，那这就是我们想要的 $g'$！

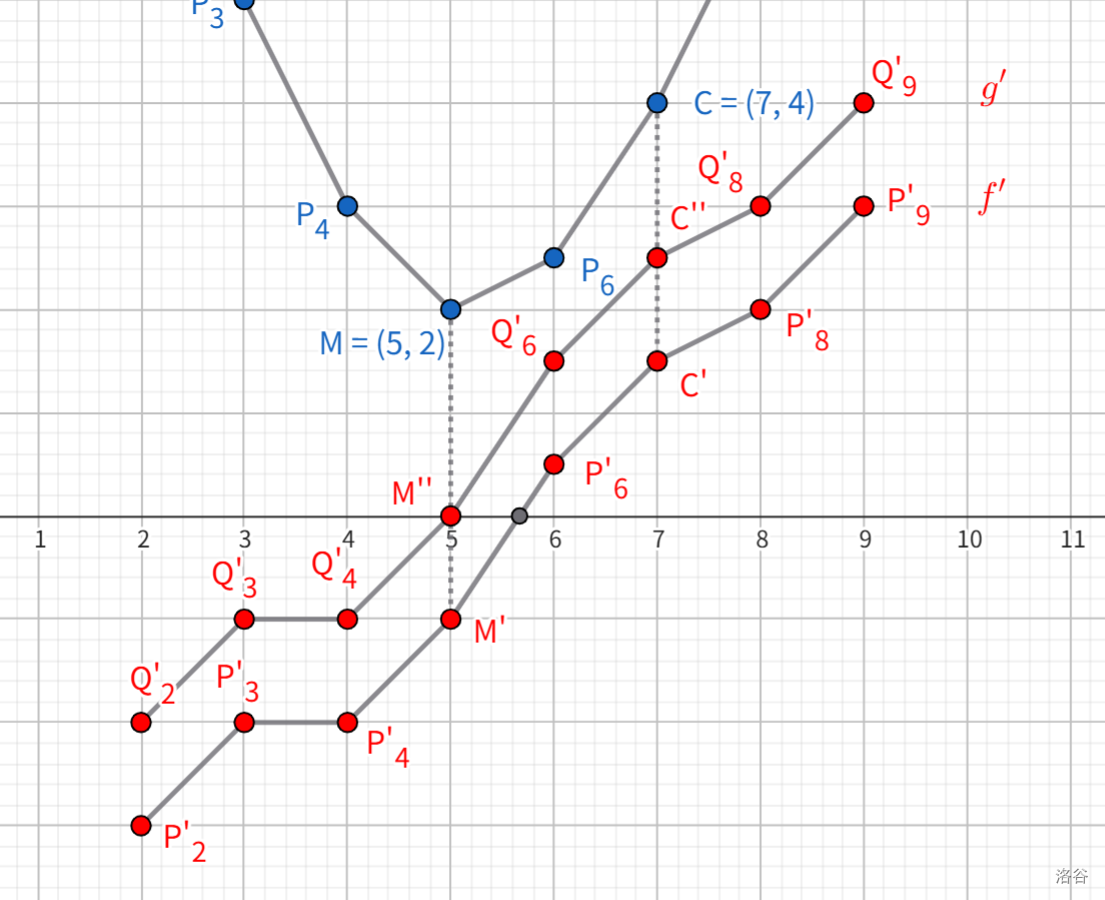
记垂直向上平移了 $k$ 个单位长度，那么有 $g'(i)=f'(i)+k$，容易想到 $g(i)=f(i)+ki$ 是一个可能的构造。并且由于 $g'$ 有 $f'$ 平移得到，仍为增函数，所以这个 $g$ 仍具有凸性！凸性是非常好的性质，加上 $g(i)=f(i)+ki$ 的形式非常简单，所以一般也可同 $f$ 一样快速计算极值和极值极值点。

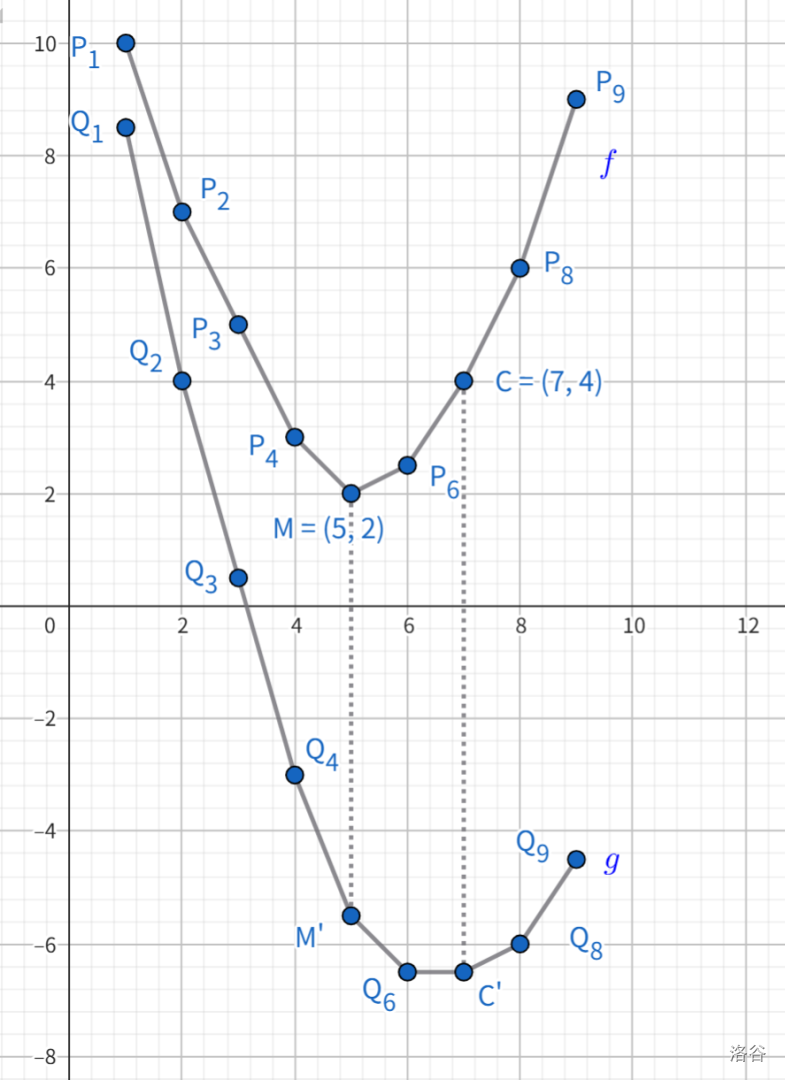
怎么完成平移的操作呢？我们二分 $k$。对每次二分的 $mid$，我们求出此时 $g$ 的极值点 $t$：

若 $t\gt c$，$f'$ 还需向上平移，$k$ 要增大；
若 $t\lt c$，$f'$ 还需向下平移，$k$ 要减小。

自己对着图像理解一下。

回到 DP 部分，当我们 check 的时候，我们需求出当前 $g$ 的最小值和最小值点，不同的是，现在不限制物品个数了！我们无需物品个数的维度，拿概述部分的例子来说：

$\text{eg.}$ 给定一数列 $a_n$，要求将其按顺序分割为 $c$ 组，使得每组的代价和最小，其中每组的代价定义为该组内所有数的和的平方。$n,c\le10^5,a_i\ge1$。

显然有 2D/1D 的 dp：设 $f_{i,j}$ 为前 $i$ 个数分了 $j$ 组的方案，答案即为 $f_{n,c}$，转移显然，预处理前缀和并滚掉第二维，时间复杂度 $\mathcal{O}(cn^2)$。斜率优化可做到 $\mathcal{O}(cn)$，但依旧无法通过。

实际上，这大部分这一类型的题目都有类似的 2D/1D dp 的做法。

容易证明它是凸的，wqs 二分可以去掉第二维，交由二分来实现。于是这个 dp 从 2D/1D 变成 1D/1D 的，我们成功实现了降维！check 里面直接写这个 dp 即可，至于极值点，转移时记录上一个状态即可。

另外，这东西本就可以斜优，所以可以做到 $O(n\log V)$，其中 $V$ 是二分值域。

wqs 二分就讲完了……吗?

3. 特殊情况：三点共线

考虑下图中三点共线的情况，那么有 $f'(c)=f'(b)$，然后你会惊讶的发现，无论如何平移都有 $f'(c)+k=f'(b)+k$，即 $a,c,b$ 三点始终共线，夹在中间的 $c$ 不可能取到最小值，怎么都二分不到！

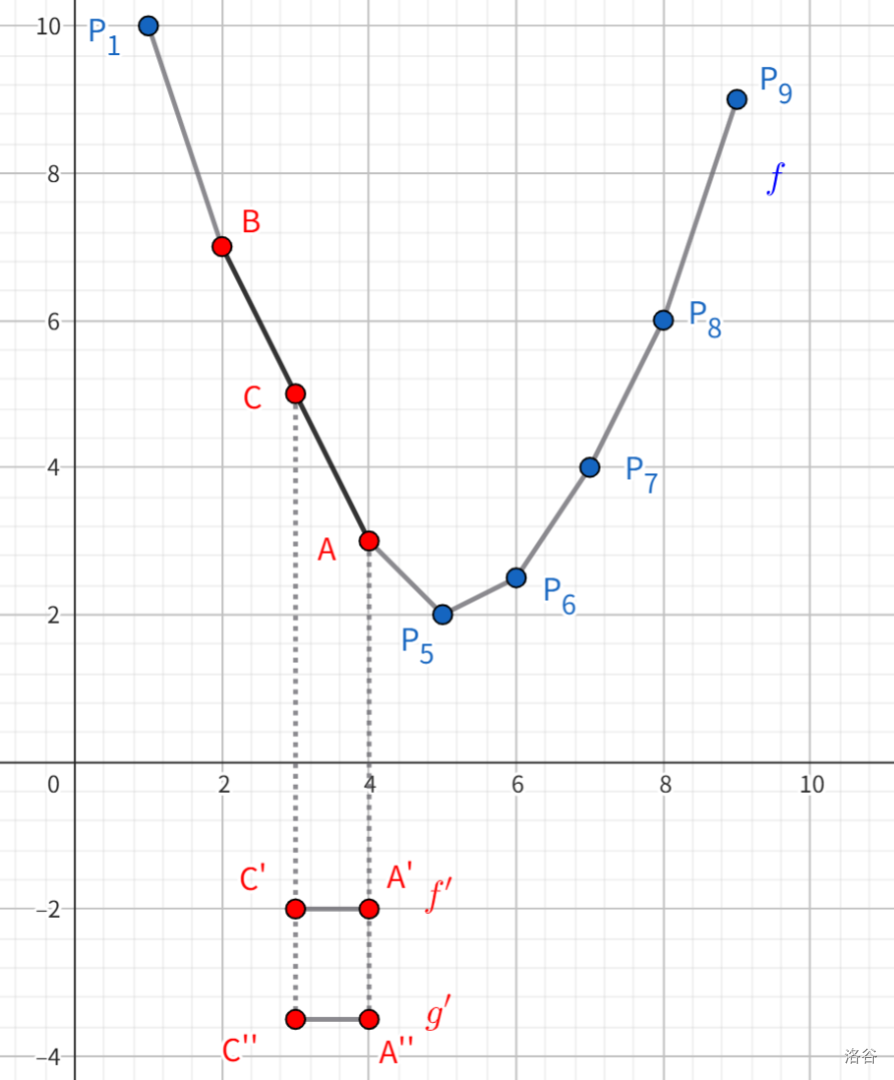
我们先二分出最小值点为 $a$ 时的 $g(a)$，解决方案是：$f(c)=g(a)-kc$，为啥？先展开：

\[f(c)=g(a)-kc=f(a)+ka-kc=f(a)+k(a-c)
\]

即：

\[f(c)-f(a)=-k\cdot(c-a)
\]

这是点斜式！我们接下来只需证明 $k_{AC}=-k$ 即可。

其实非常显然，$f'$ 经过平移的到 $g'$，且 $g'(c)=0$，那么就向上平移了 $k=-f'(c)=-k_{AC}$ 个单位长度，于是有 $k_{AC}=-k$。

怎么实现？找不到 $c$ 时，我们二分出 $c$ 右边可以取到的最接近 $c$ 的点即可。

这个问题启发我们：$k$ 貌似和凸壳上线段的斜率有一定联系，而我们知道凸壳上的斜率是单调的，不同斜率的直线在凸壳上的切点也是单调的，能不能利用这种性质来二分 $k$ 呢？

所以不好意思——还没讲完。

4. 再谈算法

4.1. 第二种理解

实际上大家在网上看到的大部分博客都是这个做法，但我觉得这个做法其实比较难抓住它的动机。

依旧讨论下凸壳。

考虑一条与下凸壳相切的斜率为 $k$ 直线 $l_k$，记其 $y$ 轴截距为 $b(k)$，过凸壳上一点 $(p,f(p))$，那么有 $f(p)=kp+b(k)$。由凸壳相切的性质，我们必然可以找到一个 $k$，使得与凸壳相切的 $l_k$ 切到点 $(c,f(c))$，这时我们只需求出 $b(k)$ 即可求出 $f(c)$。

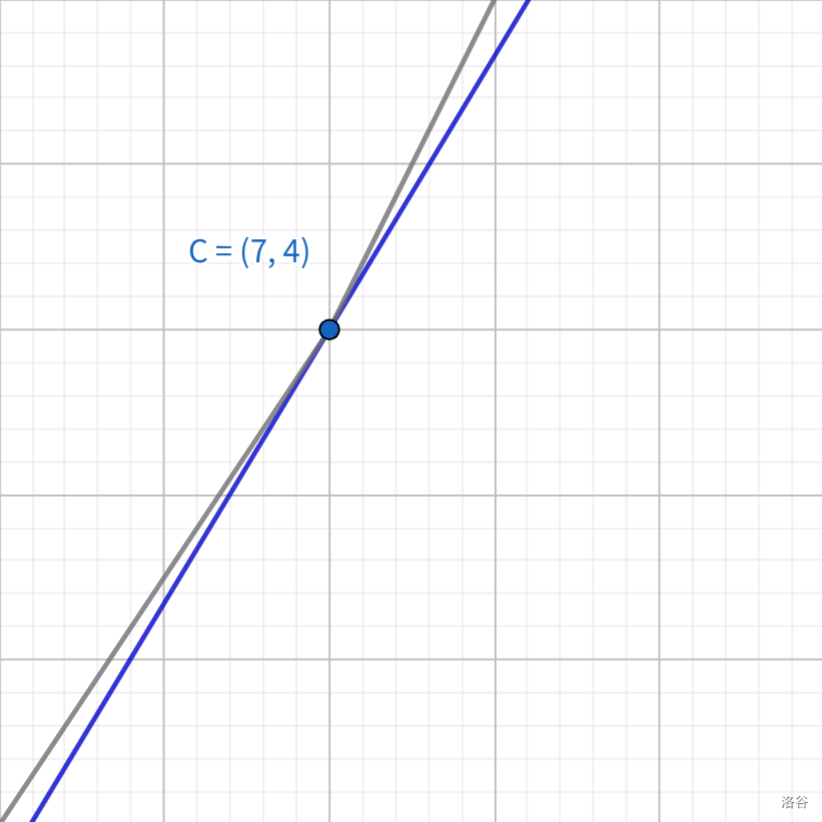
由前文所述的凸壳优秀的切点单调性（随斜率单调变化），我们直接二分 $k$，好好利用这个性质来定位 $(c,f(c))$。对于每个二分出的斜率 $mid$，我们求出切点的横坐标 $p$，并用其与 $c$ 的关系判断 $k$ 与 $mid$ 的大小关系：

若 $p\lt c$，此时切点偏左，斜率偏小，$k\gt mid$；
若 $p\gt c$，此时切点偏右，斜率偏大，$k\lt mid$。

自己对着图像理解一下。

问题转换为求切点横坐标 $p$。由相切的性质，$l$ 是所有过凸壳顶点且斜率为 $k$ 的直线中，$y$ 轴截距最小的。又 $b=y-kx$，于是有 $b(k)=\min\limits_{1\le p\le n}f(p)-kp$，且其对应的 $p$ 即为切点横坐标。

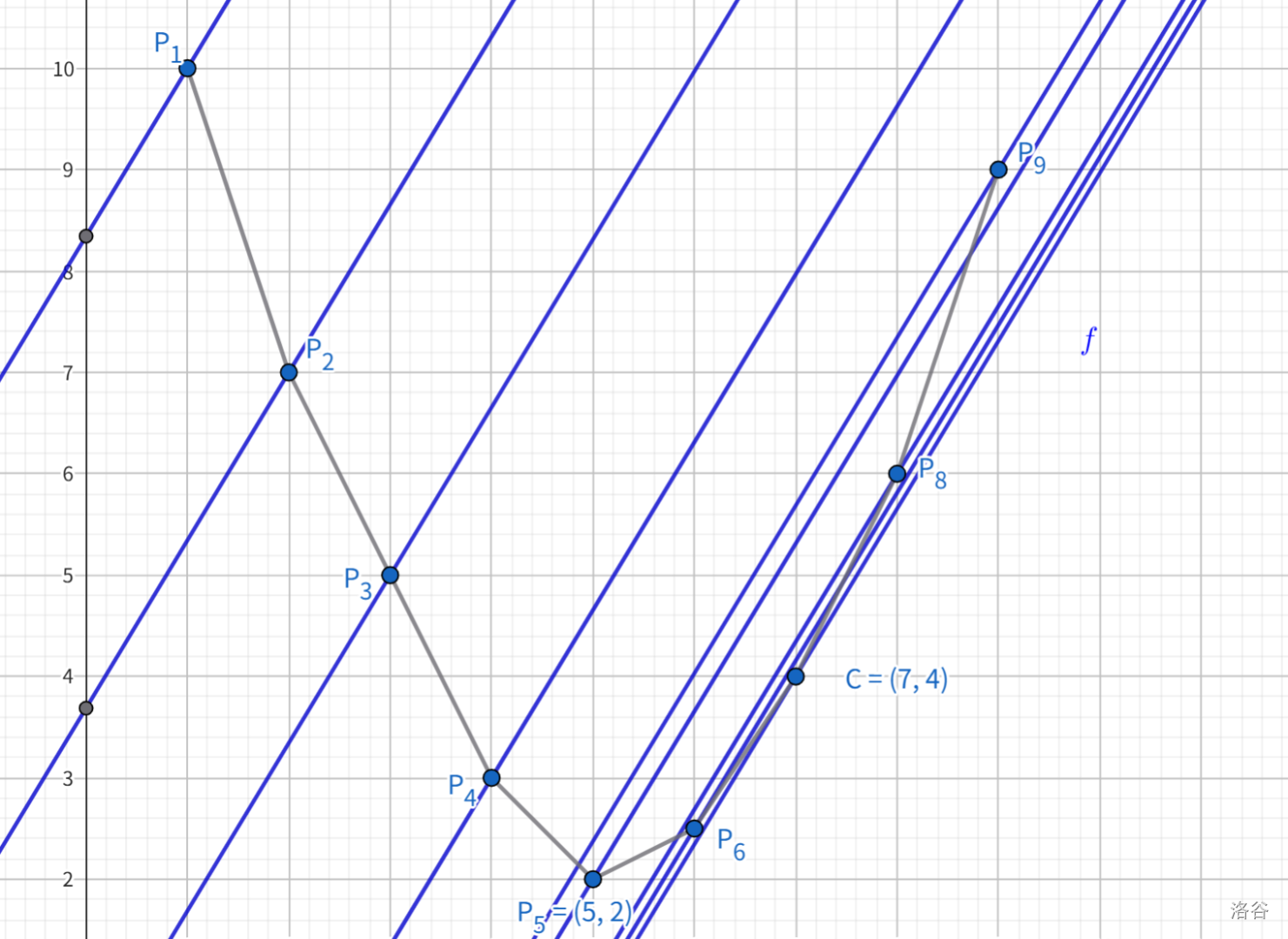
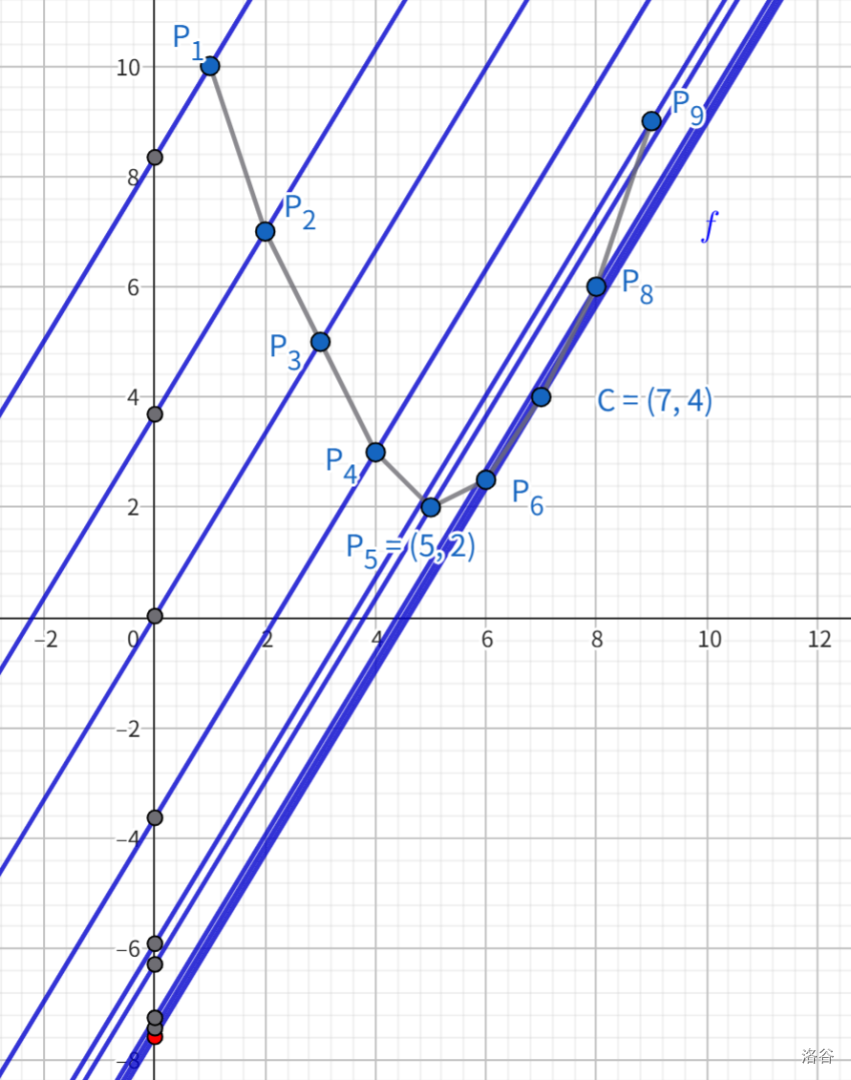
哎，这不跟第一种理解方式中的 $g(i)=f(i)+ki$ 一模一样吗！所以我们也可以快速 dp 求解这个式子，并同样通过记录上一个状态求出切点横坐标 $p$。

最后将二分的结果 $k$ 和其对应的切点横坐标 $c$ 和截距 $b(k)$ 代回 $f(p)=kp+b(k)$ 即可求出 $f(c)$。

4.2. 再论三点共线

返回来从这个角度考虑三点共线的情况。此时找不到 $c$，考虑 $c$ 右边可以取到的最接近 $c$ 的点 $a$。由于 $a$ 在 $c$ 右边，所以我们二分出切点在 $a$ 时的最小斜率，这对应的切线 $l_k$ 即为直线 $AC$。

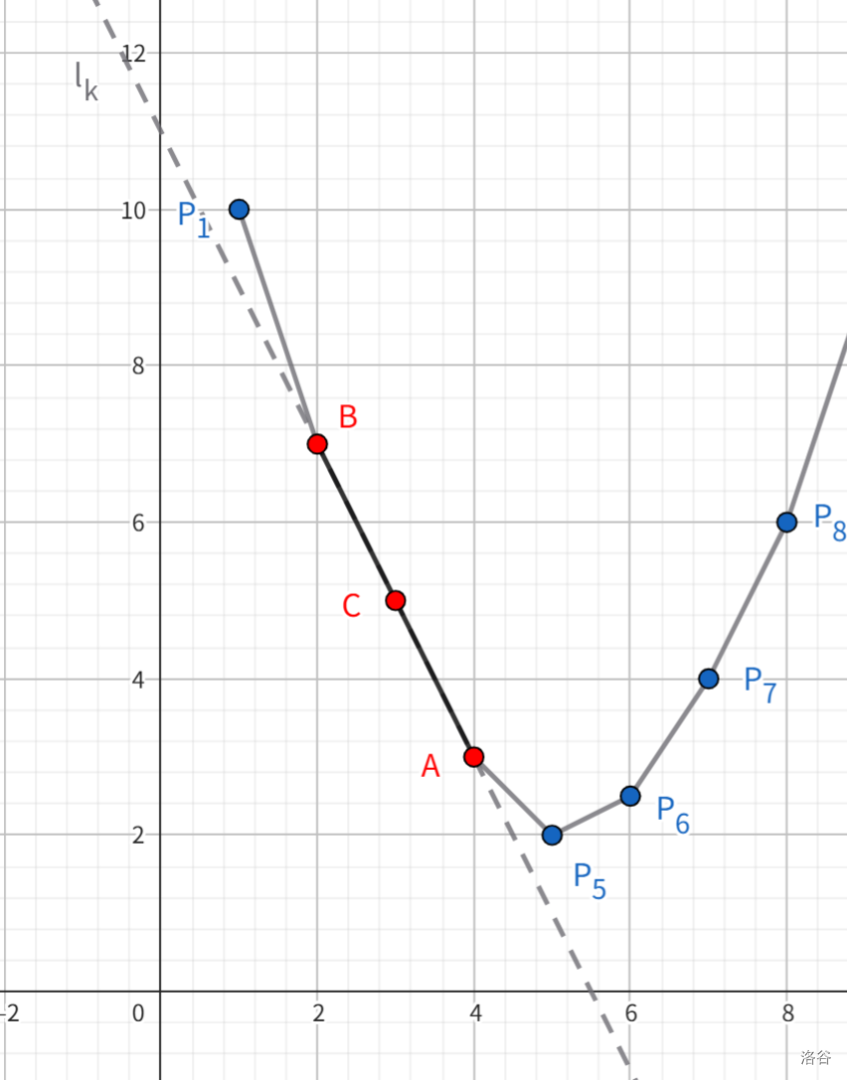
由于过 $c$，此时的 $k$ 和 $b(k)$ 都使用与 $c$，于是有 $f(c)=kc+b(k)$。

4.3. 更多细节

还没讲完，还有细节。

对三点共线情况的研究同样很有启发性。我们说 “二分出切点在 $a$ 时的最小斜率”，可以发现，当我们二分的 $k$ 恰为凸壳上相邻两个点的连线的斜率时，切线 $\bm{l_k}$ 同时切到的时凸壳的一条边而非一个点，问题就来了：它同时切到了两个（及以上，多点共线时）点，那我们应认为它对应的是哪个切点呢？这关系到我们二分调整范围的过程！

这是 wqs 二分最烦容易出错的地方，关键在于要钦定一个偏序关系。比如说，前文我们需要 “二分出切点在 $a$ 时的最小斜率”，我们就可以将这条线的斜率的贡献算到（最）靠右的点内，同时在 dp 值相等时取选择物品个数更大的那个。不管怎样，写二分的时候想好范围如何更新。

另外，大部分题目的 $f$ 为整数，所以相邻两点连线的斜率/导函数（差分）也为整数，在钦定偏序关系后必然可以二分到整数 $k$。对于需要实数二分的题目，由于每个点对应的斜率时一个区间，所以设定好精度，谨防 TLE。

5. 例题

由于笔者涉猎不深，仅能给出一些经典例题了。

6. 参考资料