「Note」数据结构方向 - 可持久化数据结构

1. 可持久化线段树

1.1. 简介

可持久化线段树一般用于解决区间第 \(k\) 小值的询问。

首先考虑简化过的问题，区间 \(\left[1,r\right]\) 的第 \(k\) 小值。

考虑用权值线段树（离散化或动态开点）来求 \(k\) 小值，接下来只需要解决区间的问题。

可持久化线段树核心思想：每次插入值时保留历史版本，来实现区间查询第 \(k\) 小。若每次修改暴力地复制一颗线段树显著不可行，考虑到每次修改最多影响 \(\log n\) 级别个数的节点，我们将这些受影响的节点分离出来进行建树，如下图（源于 OI-wiki）。



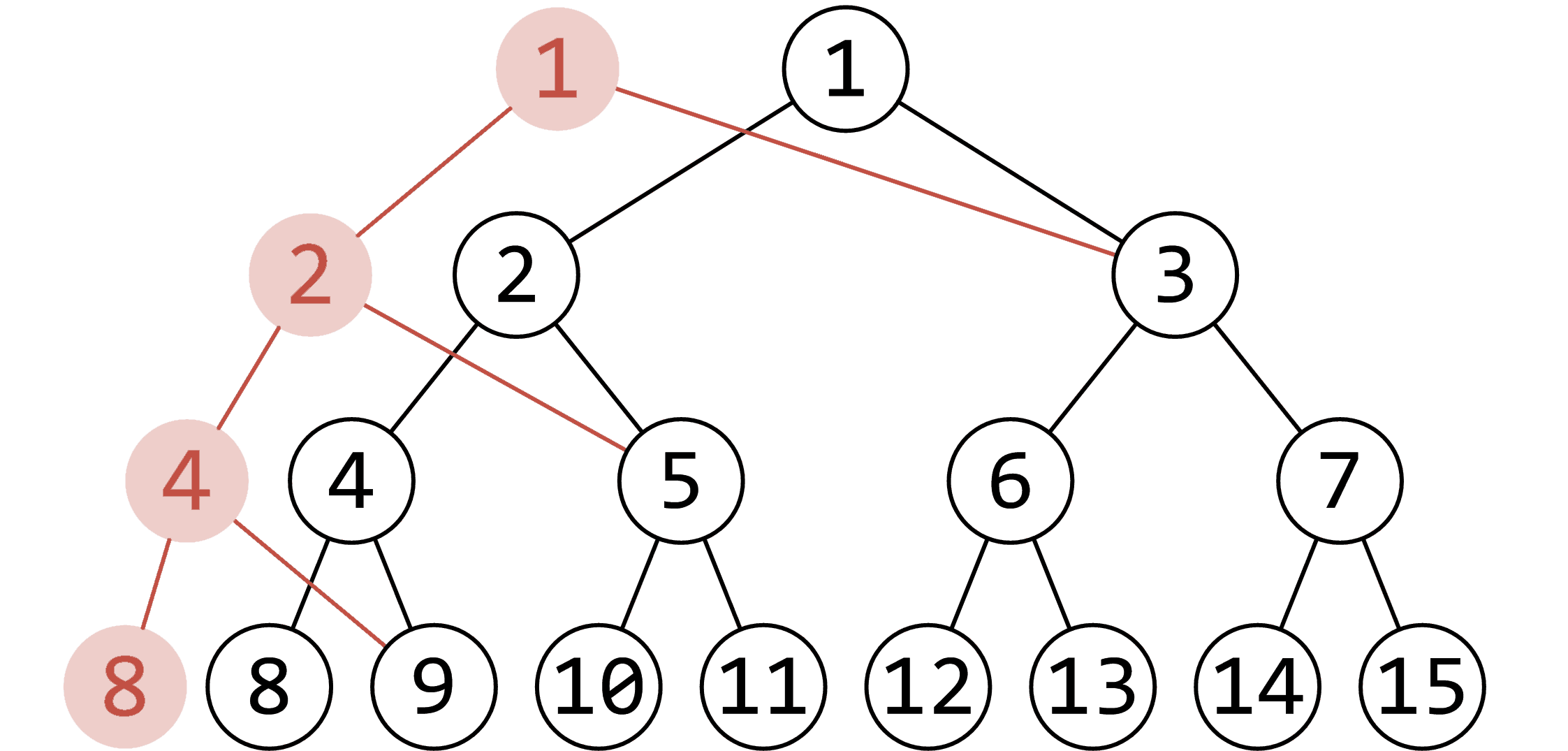
我们按顺序一个一个插入值，对于区间 \(\left[1,r\right]\) 的第 \(k\) 小值，只需要访问插入第 \(r\) 个值后的那个版本即可。

至于区间 \(\left[l,r\right]\) 的第 \(k\) 小值，只需要使用区间 \(\left[1,r\right]\) 的信息减去区间 \(\left[1,l-1\right]\) 的信息便可求出。

1.2. 例题

\(\color{royalblue}{P3834}\)

板子。

$\text{Code}$：

```
#include
#define LL long long
#define UN unsigned
using namespace std;
//--------------------//
//IO
inline int rd()
{
int ret=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9')ret=ret*10+ch-'0',ch=getchar();
return ret*f;
}
//--------------------//
const int N=2e5+5;

int n,m;

int s[N];

int tcnt,tem[N],id[N];

//--------------------//

const int TN=64e5+5;

struct Seg_Tree

{

struct Seg_Tree_Node

{

int ls,rs;

int val;

}t[TN];

int root[N],tot=0;

void build(int &rt,int L,int R)

{

rt=++tot;

if(LR)

return;

int mid=L+R>>1;

build(t[rt].ls,L,mid);

build(t[rt].rs,mid+1,R);

return;

}

void change(int &rt,int lst,int L,int R,int pos)

{

rt=++tot;

t[rt]=t[lst];

t[rt].val++;

int mid=L+R>>1;

if(LR)

return;

if(pos<=mid)

change(t[rt].ls,t[lst].ls,L,mid,pos);

else

change(t[rt].rs,t[lst].rs,mid+1,R,pos);

return;

}

int query(int rt,int pre,int L,int R,int rk)
{
	if(L==R)
		return L;
	int mid=L+R>>1;
	if(rk<=t[t[rt].ls].val-t[t[pre].ls].val)
		return query(t[rt].ls,t[pre].ls,L,mid,rk);
	return query(t[rt].rs,t[pre].rs,mid+1,R,rk-(t[t[rt].ls].val-t[t[pre].ls].val));
}

}T;

//--------------------//

int main()

{

scanf("%d%d",&n,&m);

for(int i=1;i<=n;i++)

scanf("%d",&s[i]),tem[++tcnt]=s[i];

sort(tem+1,tem+tcnt+1);

tcnt=unique(tem+1,tem+tcnt+1)-tem-1;

T.build(T.root[0],1,tcnt);

for(int temp,i=1;i<=n;i++)

{

temp=lower_bound(tem+1,tem+tcnt+1,s[i])-tem;

id[temp]=s[i];

s[i]=temp;

T.change(T.root[i],T.root[i-1],1,tcnt,s[i]);

}

for(int l,r,rk,i=1;i<=m;i++)

{

scanf("%d%d%d",&l,&r,&rk);

printf("%d\n",id[T.query(T.root[r],T.root[l-1],1,tcnt,rk)]);

}

return 0;

}

</details>