搜索算法1——聊聊dfs与回溯

搜索算法1——聊聊dfs与回溯

目录

1.dfs 的概念

$\ \ \ $1.1 dfs 的概念

2.dfs 的做法

$\ \ \ $2.1 为什么要用 dfs

$\ \ \ $2.2 dfs 如何实现

$\ \ \ $2.3 复杂度分析

3. 回溯法

$\ \ \ $3.1 回溯法的概念

$\ \ \ $3.2 回溯法的实现

1.dfs的概念

1.1.dfs的概念

dfs，即深度优先搜索，顾名思义，深度优先，就是不撞南墙不回头，它每一次都会尝试向更深的节点走。

在搜索里，dfs 一般指的是递归函数实现的暴力枚举，一般时间复杂度是 \(O(!n)\)。

对于在图论里的 dfs，这一章并不会介绍，有兴趣的可以跳伞 此处待补。

2.dfs的做法

2.1.为什么要用dfs

我们看一道例题：

输入正整数 \(n\)，输出由 \(1\) 到 \(n\) 这 \(n\) 个数取出 \(k\) 个 \((1\le n\le 10,1\le k\le n)\) 的所有组合。

如果不用 dfs，那么这题该怎么办呢？

循环呗。

\(k\) 重循环枚举选哪个数，判断重不重复，然后输出即可。

但是这样复杂度太超标了，足足有 \(O(n^k)\)，最高有 \(O(10^{10})\)！

那么，就需要 dfs 来解决这个问题了。

2.2.dfs如何实现

我们可以先模拟一个样例：

\(n=4,k=2\)

我们可以发现，用 2.1 中说的算法，过程如下（设第一重循环变量为 \(i\)，第二重循环变量为 \(j\)）：

i=1,j=1,重复,跳过
i=1,j=2,输出
i=1,j=3,输出
i=1,j=4,输出
i=2,j=1,重复,跳过
i=2,j=2,重复,跳过
i=2,j=3,输出
i=2,j=4,输出
i=3,j=1,重复,跳过
i=3,j=2,重复,跳过
i=3,j=3,重复,跳过
i=3,j=4,输出
i=4,j=1,重复,跳过
i=4,j=2,重复,跳过
i=4,j=3,重复,跳过
i=4,j=4,重复,跳过

其实，我们完全可以不遍历这些重复的，以节约时间。

我们可以把枚举"选哪个数"，变成"枚举数"。

比如，我们可以先枚举到 \(1\)，然后延伸出两个分支——\(1\) 选和 \(1\) 不选。

然后这两个分支分别往下枚举又能分别延伸出两个分支——\(2\) 选和 \(2\) 不选。

以此类推。

我们就可以画出类似于这样的一张图：

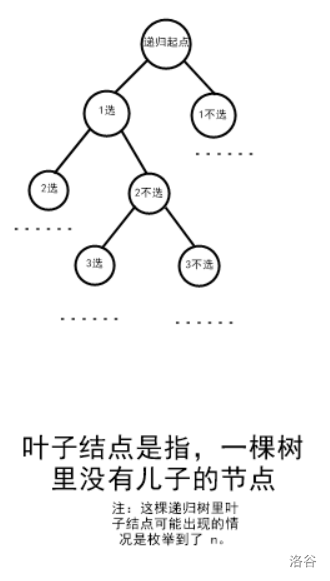
这就是递归树（例子为 \(k=2\)）。

那么我们就知道了，我们可以从 \(1\) 开始枚举，枚举到 \(n\)，每一个数有两种方案：选或不选，然后如果选了 \(k\) 个数就输出。

但是，选或不选该怎么实现呢？

这就要用到 dfs 了。

dfs 是通过重复调用一个函数来实现的，例如：

void dfs(int dep,int cnt)//dep是当前枚举到的数,cnt是选了几个数
{
    if(dep==n+1)
    {
        if(cnt==k)
        {
            for(int i=0;i<cnt;i++)
            {
                printf("%d ",a[i]);//a[i]是记录的选的数的集合
            }
        }
        return;//只枚举到n,此处return是为了不继续枚举
    }
    a[cnt]=dep;//这里如果选的话,那么后面cnt+1,dep就存在集合里了,就完成了“选”这一操作.反之,如果不选,那么cnt不变,后面枚举到的dep就覆盖了a[cnt],达到不选的效果
    dfs(dep+1,cnt+1);//dep选
    dfs(dep+1,cnt+1);//dep不选
}

（注释已经很详细了，应该不用再讲了吧）

2.3.复杂度分析

dfs 无剪枝复杂度一般都是 \(O(!n)\) 级别的。

记住就行。

3.回溯法

3.1.回溯法的概念

回溯法的本质就是对于一棵递归树，程序在遍历时，如果发现遇到了边界条件，就可以回去，搜另外的链。

3.2.回溯法的实现

看例题。

输入正整数 \(n\)，输出由 \(1\) 到 \(n\) 这 \(n\) 个数 \((n\le 7)\) 的所有排列，每行一个排列，数与数之间有一个空格，两个排列中，第一个数小的优先输出，第一个数相同，比较第二个数，后面以此类推。

对于这一题，如果我们再用上面的方法，就会漏选。

而由于是 \(n\) 个数选 \(n\) 个，所以我们甚至不用 \(cnt\)，只记录 \(dep\) 即可。

那么回溯怎么实现呢？

看代码（解析都在注释里）：

void dfs(int dep)
{
	if(dep==n+1)//就是到达了边界条件,这里直接输出就行
	{
		for(int i=1;i<=n;i++)
		{
			printf("%d ",a[i]);
		}
		cout<<endl;
		return;
	}
	for(int i=1;i<=n;i++)
	{
		if(!biao[i])//表示i没被选
		{
			biao[i]=1;//选i
			a[dep]=i;
			dfs(dep+1);//往下递归
			biao[i]=0;//这就是回溯的关键一步,这一行代码目的在于在接着进行for循环时,不能被这一次遍历到的i干扰,否则就会出现n个数选不完的情况
		}
	}
}

（也不讲了，这个已经很详细了）

好了，那么搜索算法1就结束了，感谢大家的支持，我是_little_Cabbage_，我们搜索算法2再见！