Python中指数概率分布函数的绘图详解

在数据科学和统计学中，指数分布是一种应用广泛的连续概率分布，通常用于建模独立随机事件发生的时间间隔。通过Python，我们可以方便地计算和绘制指数分布的概率密度函数（PDF）。本文将详细介绍指数分布的原理、应用场景，并提供详细的代码示例，展示如何在Python中绘制指数分布的概率密度函数图。

一、指数分布的理论概述

1. 定义与公式

指数分布是一种描述随机变量在一个固定底数上的对数值的分布情况，或者在概率理论和统计学中，用于描述泊松过程中事件之间的时间间隔的概率分布。具体来说，它表示事件以恒定平均速率连续且独立地发生的过程。

指数分布的概率密度函数（PDF）为：

f(x;λ)=λ**e−λ**x

其中，λ>0 是分布参数，表示单位时间内的平均发生次数（即速率），x≥0 是随机变量，表示事件发生的时间间隔或等待时间。

指数分布的累积分布函数（CDF）为：

F(x;λ)=1−e−λ**x

这个公式表示在x时间或更短时间内事件发生的概率。

2. 关键性质

• 无记忆性：无论过去发生了什么，未来事件发生的概率仅取决于时间间隔的长度，而与起始时间无关。这种特性使得指数分布在描述某些具有“马尔可夫性”的随机过程时特别适用。
• 单调递减：指数分布的概率密度函数是单调递减的，且当x趋近于无穷大时，概率密度趋近于零。这意味着随着事件间隔时间的增加，该事件再次发生的概率逐渐降低。
• 期望与方差：指数分布的期望值和方差均为λ1，这一性质使得我们可以通过简单的计算来预测事件发生的平均时间和波动情况。

3. 应用场景

• 可靠性工程：用于描述电子元器件、机械设备等复杂系统的故障时间分布。
• 排队论：用于分析服务系统中顾客到达时间间隔的分布，如银行、医院等服务窗口的顾客到达情况。
• 生物统计学：用于描述生物种群中某些事件（如疾病发生、生育等）的时间间隔分布。
• 网络通信：用于建模数据传输过程中的延迟时间分布。
• 金融分析：用于分析金融市场中的某些随机事件，如股票价格的波动等（尽管实际应用中可能需要更复杂的模型）。

二、Python中绘制指数分布图的步骤

在Python中，我们可以使用numpy库来处理数值运算，使用matplotlib库来绘制图形，还可以使用scipy库中的stats模块来计算和绘制指数分布函数。

1. 导入必要的库

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

2. 定义参数并生成数据点

我们需要定义指数分布的速率参数λ，并生成一组用于绘制概率密度函数的数据点。

# 定义参数 lambda
lambda_param = 1.5

# 生成 0 到 5 之间的 100 个数据点
x = np.linspace(0, 5, 100)

3. 计算概率密度函数（PDF）

使用指数分布的公式来计算每个数据点的概率密度。

# 计算概率密度函数
pdf = lambda_param * np.exp(-lambda_param * x)

4. 绘制图形

使用matplotlib库来绘制计算得到的概率密度图。

# 创建绘图
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label='Exponential PDF', color='blue')
plt.title('Exponential Probability Density Function')
plt.xlabel('x')
plt.ylabel('PDF')
plt.legend()
plt.grid(True)

# 显示图形
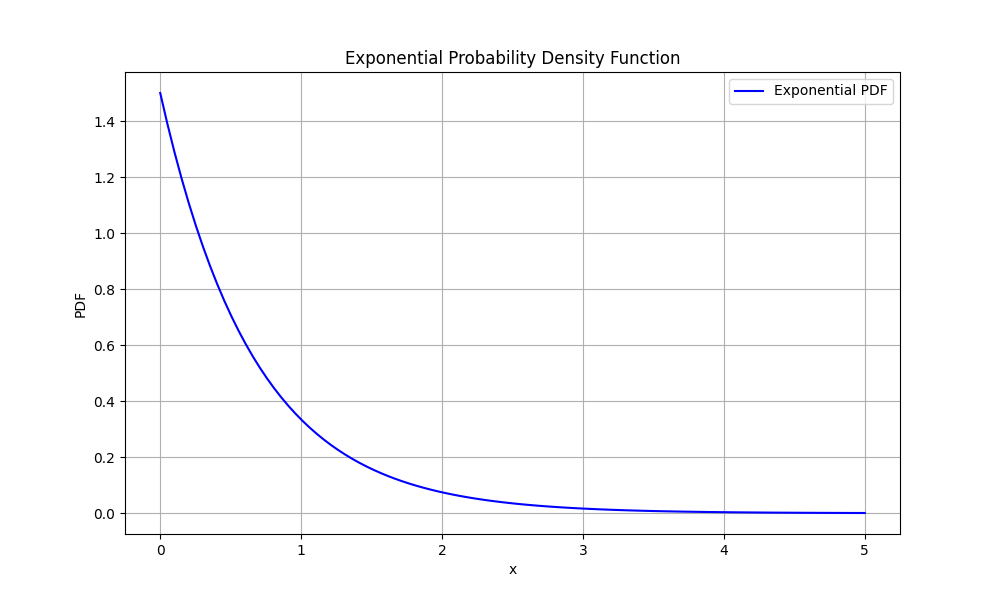
plt.show()

运行结果如下：

5. 使用scipy库计算和绘制指数分布函数

除了手动计算PDF外，我们还可以使用scipy库中的expon函数来更方便地计算和绘制指数分布函数。

# 创建指数分布对象
rate = 2
dist = expon(scale=1/rate)

# 计算概率密度
x = 1
pdf = dist.pdf(x)
print(f"PDF at x={x}: {pdf}")

# 计算累积概率
x = 3
cdf = dist.cdf(x)
print(f"CDF at x={x}: {cdf}")

# 生成随机样本
samples = dist.rvs(size=1000)

# 绘制直方图
plt.hist(samples, bins=30, density=True, alpha=0.7)
plt.xlabel('x')
plt.ylabel('Probability')
plt.title('Exponential Distribution')
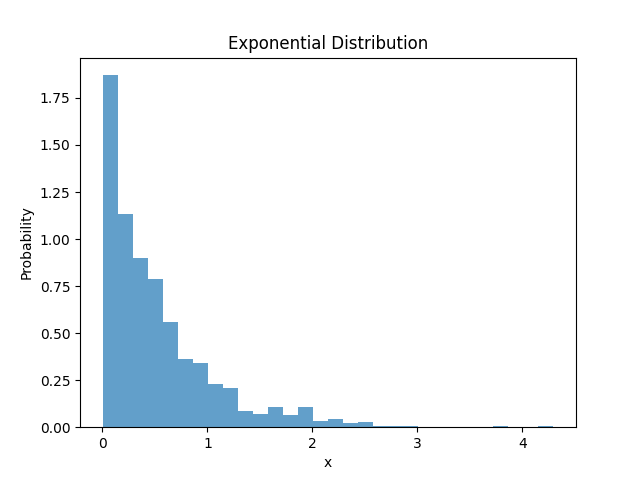
plt.show()

运行结果如下：

三、完整代码示例

将上述步骤整合起来，我们得到一个完整的代码示例，用于绘制指数分布的概率密度函数图。

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

# 定义参数 lambda
lambda_param = 1.5

# 生成 0 到 5 之间的 100 个数据点
x = np.linspace(0, 5, 100)

# 计算概率密度函数
pdf = lambda_param * np.exp(-lambda_param * x)

# 创建绘图
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label='Exponential PDF', color='blue')
plt.title('Exponential Probability Density Function')
plt.xlabel('x')
plt.ylabel('PDF')
plt.legend()
plt.grid(True)

# 显示图形
plt.show()

# 使用scipy库计算和绘制指数分布函数
# 创建指数分布对象
rate = 2
dist = expon(scale=1/rate)

# 计算概率密度
x = 1
pdf = dist.pdf(x)
print(f"PDF at x={x}: {pdf}")

# 计算累积概率
x = 3
cdf = dist.cdf(x)
print(f"CDF at x={x}: {cdf}")

# 生成随机样本
samples = dist.rvs(size=1000)

# 绘制直方图
plt.hist(samples, bins=30, density=True, alpha=0.7)
plt.xlabel('x')
plt.ylabel('Probability')
plt.title('Exponential Distribution')
plt.show()

四、总结

指数分布作为一种重要的连续概率分布，在描述具有恒定发生速率和独立性的随机事件方面具有广泛的应用。通过Python，我们可以方便地计算和绘制指数分布的概率密度函数图，从而更直观地理解随机事件的时间分布特性。本文详细介绍了指数分布的原理、关键性质、应用场景，并提供了详细的代码示例，展示了如何在Python中绘制指数分布的概率密度函数图。希望这些内容能为读者提供有价值的参考和实际应用指导。

五、实际的例子

当然，以下我将提供几个实际的例子，并附上可以直接运行的Python代码示例。这些例子将涵盖指数分布在可靠性工程、排队论和泊松过程中的应用。

1. 可靠性工程：电子设备的故障时间分布

假设某型电子设备的故障时间服从参数为λ=0.01（即平均无故障时间为100小时）的指数分布。我们可以使用Python来模拟这种分布，并计算设备的可靠性函数。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

# 定义参数
lambda_param = 0.01  # 故障率（1/小时）
mean_ttf = 1 / lambda_param  # 平均无故障时间（小时）

# 生成故障时间数据
ttf_samples = expon.rvs(scale=mean_ttf, size=1000)  # 从指数分布中抽取样本

# 绘制故障时间分布的直方图
plt.hist(ttf_samples, bins=30, density=True, alpha=0.6, color='blue', edgecolor='black')

# 绘制指数分布的概率密度函数
x = np.linspace(0, 4*mean_ttf, 1000)
pdf = expon.pdf(x, scale=mean_ttf)
plt.plot(x, pdf, 'r-', lw=2, label='Exponential PDF')

plt.xlabel('Time to Failure (hours)')
plt.ylabel('Probability Density')
plt.title('Failure Time Distribution of Electronic Device')
plt.legend()
plt.grid(True)
plt.show()

# 计算并绘制可靠性函数
reliability = expon.sf(x, scale=mean_ttf)  # 生存函数（1-CDF）
plt.plot(x, reliability, 'g-', lw=2, label='Reliability Function')
plt.xlabel('Time (hours)')
plt.ylabel('Reliability')
plt.title('Reliability Function of Electronic Device')
plt.legend()
plt.grid(True)
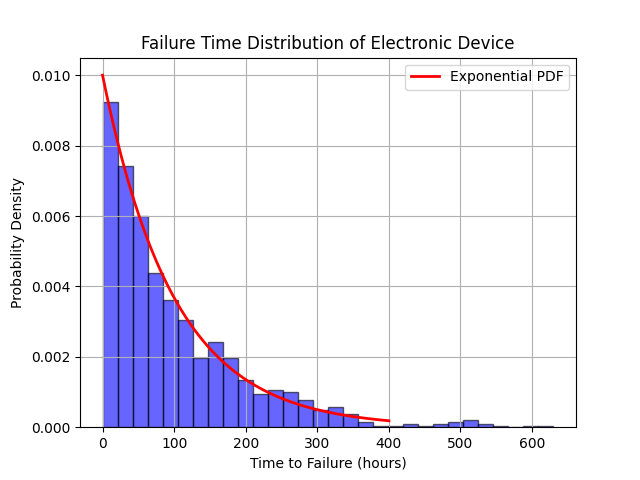
plt.show()

运行结果如下：

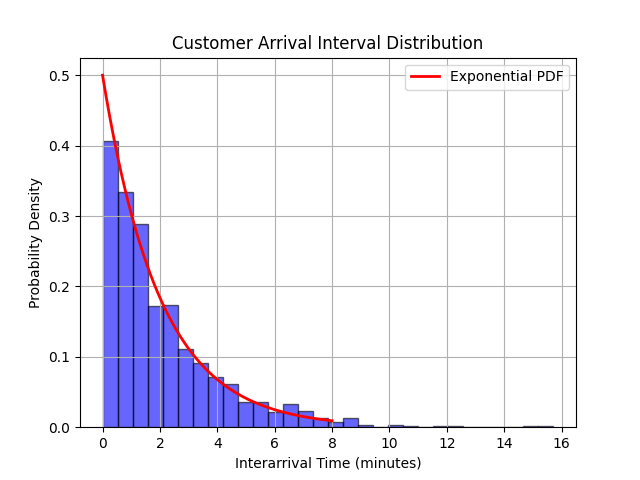
2. 排队论：顾客到达时间间隔分布

假设一个银行服务窗口的顾客到达时间间隔服从参数为λ=0.5（即平均到达间隔为2分钟）的指数分布。我们可以使用Python来模拟这种分布，并计算服务窗口的利用率。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

# 定义参数
lambda_param = 0.5  # 顾客到达率（顾客/分钟）
mean_interarrival_time = 1 / lambda_param  # 平均到达间隔（分钟）

# 生成顾客到达时间间隔数据
interarrival_times = expon.rvs(scale=mean_interarrival_time, size=1000)  # 从指数分布中抽取样本

# 绘制顾客到达时间间隔分布的直方图
plt.hist(interarrival_times, bins=30, density=True, alpha=0.6, color='blue', edgecolor='black')

# 绘制指数分布的概率密度函数
x = np.linspace(0, 4*mean_interarrival_time, 1000)
pdf = expon.pdf(x, scale=mean_interarrival_time)
plt.plot(x, pdf, 'r-', lw=2, label='Exponential PDF')

plt.xlabel('Interarrival Time (minutes)')
plt.ylabel('Probability Density')
plt.title('Customer Arrival Interval Distribution')
plt.legend()
plt.grid(True)
plt.show()

# 假设服务时间为常数（例如，每位顾客平均服务5分钟）
service_time = 5  # 服务时间（分钟）

# 计算服务窗口的利用率（ρ = λ * 服务时间 / (λ * 服务时间 + 1)）
utilization = lambda_param * service_time / (lambda_param * service_time + 1)
print(f"Service Window Utilization: {utilization:.2f}")

运行结果如下：

3. 泊松过程：电话呼叫到达的等待时间分布

假设电话呼叫到达的过程是一个泊松过程，其到达率为λ=3（即平均每分钟有3个呼叫到达）。我们可以使用Python来模拟这种泊松过程，并计算相邻呼叫到达的等待时间分布。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

# 定义参数
lambda_param = 3  # 呼叫到达率（呼叫/分钟）
mean_interarrival_time = 1 / lambda_param  # 平均到达间隔（分钟）

# 生成泊松过程的到达时间（累积和）
arrival_times = np.cumsum(expon.rvs(scale=mean_interarrival_time, size=1000))  # 从指数分布中抽取样本并累积和

# 计算相邻呼叫到达的等待时间
waiting_times = np.diff(arrival_times, prepend=0)  # 在数组前面添加一个0来计算第一个呼叫的等待时间（实际上为0）

# 绘制等待时间分布的直方图
plt.hist(waiting_times, bins=30, density=True, alpha=0.6, color='blue', edgecolor='black')

# 绘制指数分布的概率密度函数
x = np.linspace(0, 4*mean_interarrival_time, 1000)
pdf = expon.pdf(x, scale=mean_interarrival_time)
plt.plot(x, pdf, 'r-', lw=2, label='Exponential PDF')

plt.xlabel('Waiting Time (minutes)')
plt.ylabel('Probability Density')
plt.title('Waiting Time Distribution of Phone Calls')
plt.legend()
plt.grid(True)
plt.show()

运行结果如下：

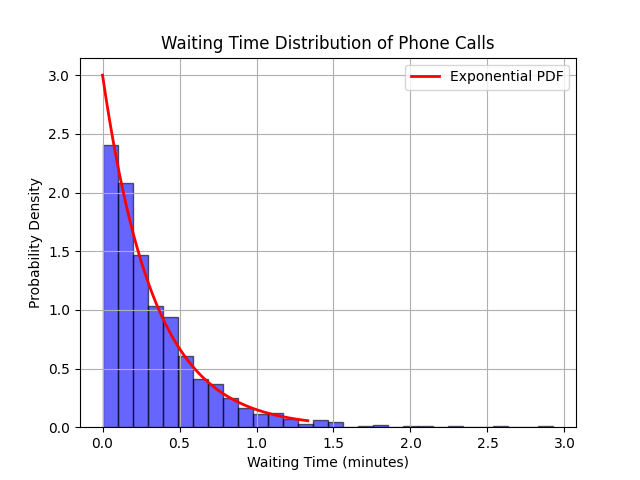
以上代码示例展示了如何使用Python中的numpy和scipy.stats库来模拟指数分布，并计算相关的统计量。这些示例涵盖了可靠性工程、排队论和泊松过程中的应用场景，并提供了可以直接运行的代码。