代码随想录第十四天 | Leecode 103. 二叉树的层序遍历、226. 翻转二叉树、101. 对称二叉树、104. 二叉树的最大深度、111. 二叉树的最小深度

写在前面

今天补一下昨天没有写的层序遍历，层序遍历有整整十道题，打算只在博客详细写一道，后续的题目就自己在Leecode上刷一刷得了，不准备全部写下来（计划是只在博客给出每一道题目的链接）。除此之外还有今天的四道题目，准备都用递归来实现。

Leecode 102. 二叉树的层序遍历

• https://leetcode.cn/problems/binary-tree-level-order-traversal/description/

题目描述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

• 示例 1：

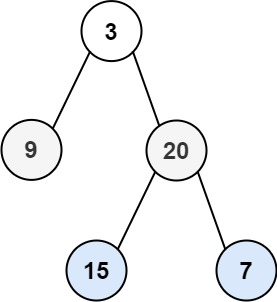
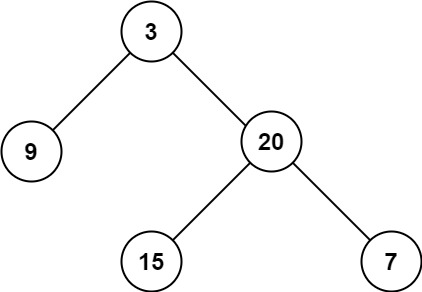
输入：root = [3,9,20,null,null,15,7]

输出：[[3],[9,20],[15,7]]

• 示例 2：

输入：root = [1]

输出：[[1]]

• 示例 3：

输入：root = []

输出：[]

解法1 使用队列存放节点指针和深度进行迭代

层序遍历的顺序就和队列的先进先出的顺序是一致的，我们只需要每次访问一个节点的时候，依次将其左右子节点入队（如果有的话），随后每次都访问节点都是从队列中pop出队列中第一个节点。这样的顺序就是按层遍历的顺序。

但我们仅有这样的顺序还不够解决这道题目，因为要求输出的结果是一个vector<vector<int>>类型的二维数组，即我们不光要知道按层遍历的节点顺序，同时还需要知道每个节点所在的深度。由此才能将每个节点准确地放在二维数组中对应的位置。

为此可以考虑使用队列存放一个<TreeNode* curNode, int curDep>类型的数据对，其中包含了节点的指针，及其所在的深度。只需要在每个节点指针入队的时候同时保存其所在深度，那么后续就可以将其准确地存放于result二维数组中。由此我们可以得到如下代码：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        queue<pair<TreeNode*,int>> nodeQue; // 使用队列来保存节点指针和节点所在深度的pair
        if(root) nodeQue.push({root,0}); // 确保root不为空，如果root为空则初始队列为空，后续不会进入循环
        while(!nodeQue.empty()){
            TreeNode* curNode = nodeQue.front().first; // 当前节点指针为队列第一个数据对的first
            int curDep = nodeQue.front().second; // 当前节点所在深度为队列第一个数据对的second
            nodeQue.pop(); // 第一个元素出队
            if(curNode->left) nodeQue.push({curNode->left, curDep+1}); // 将当前节点的左右子节点入队（如果存在的话）
            if(curNode->right) nodeQue.push({curNode->right, curDep+1});
            if(curDep == result.size()) result.push_back({}); // 需要对result动态扩容，否则下一行中result[curDep]可能不存在，直接push_back会导致访问越界
            result[curDep].push_back(curNode->val); // 在result中记录当前节点，需要根据深度在对应的位置push_back
        }
        return result;
    }
};

上面使用有节点和所在深度组成的数据对可以实现保留深度的按层遍历，但这种在队列中同时存放节点指针和深度的方法可能会带来更多的内存开销。而这种深度信息其实可以通过其他方式来实现，而不必专门占用空间来存放。接下来介绍一种利用循环来实现深度的方法。

解法2 双层循环迭代表示深度（层序遍历标准方法）

考虑使用双层循环，外层循环用于遍历整颗树，直至队列为空则结束。而内层循环用于遍历某一层，由于某层刚开始遍历的时刻的队列长度，恰好就是该层的长度，因此只需此时记录下当前队列长度，按照这个次数进行循环记录该层节点的值，同时将每个节点的左右子节点再存入队列中（如果有子节点的话）；这样即可得到某一层按层遍历的vector向量，再将这个向量整体push到二维数组中即可。具体代码如下：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        queue<TreeNode*> nodeQueue;
        if(root) nodeQueue.push(root);
        while(!nodeQueue.empty()){
            int levelSize = nodeQueue.size(); // 记录当前层的长度
            vector<int> curVec; // 当前层的节点的值向量
            for(int i = 0; i < levelSize; i++){
                TreeNode* curNode = nodeQueue.front();
                if(curNode->left) nodeQueue.push(curNode->left);
                if(curNode->right) nodeQueue.push(curNode->right);
                curVec.push_back(curNode->val);
                nodeQueue.pop();
            }
            result.push_back(curVec); // 将当前层的遍历结果放入二维数组中
        }
        return result;
    }
};

上面代码中，对于内层的for循环，每次循环就相当于是对一层进行操作，此时自然就包含了当前所在层的信息，从而可以不必使用多余的内存存储当前所在层的序号。

解法3 递归实现层序遍历

对于二叉树而言，很多时候都能使用递归来实现。而本题中的层序遍历也同样可以使用递归来实现。具体代码如下：

class Solution {
public:
    void levelOrderHelper(TreeNode* curNode, vector<vector<int>>& vec, int depth){ // 递归辅助函数
        if(curNode == nullptr) return; // 如果当前节点为空，则说明已经到最底层，直接返回
        if(vec.size() == depth) vec.push_back({}); // 对二维向量扩容
        vec[depth].push_back(curNode->val); // 将当前节点放入二维向量中对应的位置
        levelOrderHelper(curNode->left, vec, depth+1); // 递归调用左子树
        levelOrderHelper(curNode->right, vec, depth+1); // 递归调用右子树
    }

    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        levelOrderHelper(root, result, 0); // 递归调用根节点，此时深度为0，将结果存放于result中
        return result;
    }
};

上面递归实现层序遍历，其实本质上是在先序遍历的基础上修改而来的。由于先序遍历和层序遍历在一定程度上具有相似性，例如当只有三个节点的时候，先序和层序的顺序都是“根、左、右”。所以如果要将其更改为层序遍历，只需要在先序遍历的基础上（递归调用顺序都是先处理当前节点，再分别递归调用左、右节点），添加当前所在层深度，遍历后将节点放到二维向量对应深度的位置即可。

层序遍历相关题目

层序遍历这部分有很多题目，除了上面展示的这道之外的题目准备就自己刷完就好，就不再一一在博客中详细解读了，在这里只留下这些题目的链接并简单说明思路，读者（如果有的话）可以自行点击前往刷题：

• Leecode 107. 二叉树的层序遍历 II: https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/description/
  • 这道题只需要将原本层序遍历的结果进行一次reverse即可，但要注意reverse的用法是reverse(result.begin(),result.end());
• Leecode 199. 二叉树的右视图: https://leetcode.cn/problems/binary-tree-right-side-view/description/
  • 只在完成一层的遍历之后，再进行push_back()记录当前层最后一个节点的值
• Leecode 637. 二叉树的层平均值: https://leetcode.cn/problems/average-of-levels-in-binary-tree/description/
  • 在每一层内遍历的时候将当前节点的值加到一个int类型变量上，最后在遍历完一层之后用该层求和结果除以该层的节点个数
• Leecode 429. N 叉树的层序遍历：https://leetcode.cn/problems/n-ary-tree-level-order-traversal/description/
  • N叉树中每个节点用了一个vector类型的children来存储，每次遍历节点的时候，需要多加一个for循环来遍历children中的所有子节点将其入队即可
• Leecode 515. 在每个树行中找最大值：https://leetcode.cn/problems/find-largest-value-in-each-tree-row/description/
  • 用一个int变量存储每一层的最大值，初始值设置为每一层第一个树的值，即开始遍历该层时队列front处的值；遍历同时做判断，如果当前节点的值更大则更新max的值
• Leecode 116. 填充每个节点的下一个右侧节点指针：https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/description/
  • 层内遍历的for循环内新增一个判断，如果当前i < size - 1（即只要不是本行最后一个节点），则需要将next指向此时队列头的节点（前提是要先将当前节点pop出队）
• Leecode 117. 填充每个节点的下一个右侧节点指针 II：https://leetcode.cn/problems/populating-next-right-pointers-in-each-node-ii/description/
  • 和上一题一模一样，因为上一题并没有考虑其为完全二叉树，而只是将其看做一般二叉树，因此代码完全一致，直接复制粘贴即可
• Leecode 104. 二叉树的最大深度：https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/
  • 定义一个深度int变量depth初始为0，接下来进行按层遍历，while循环内每进行一次就说明当前层还有节点，进行一次depth++。最后输出返回depth即可
• Leecode 111. 二叉树的最小深度：https://leetcode.cn/problems/minimum-depth-of-binary-tree/description/
  • 和上面一样定义一个int类型的depth变量，在每层遍历的for循环中，增加一个判断，如果左右子节点都为空，则返回此时的depth；最后再返回depth就可以实现了

至此已经连续刷完十道层序遍历的题目，一连十道下来总用时不到两小时，真的太爽了。

Leecode 226. 翻转二叉树

• 题目链接：https://leetcode.cn/problems/invert-binary-tree/description/

题目描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

• 示例 1：

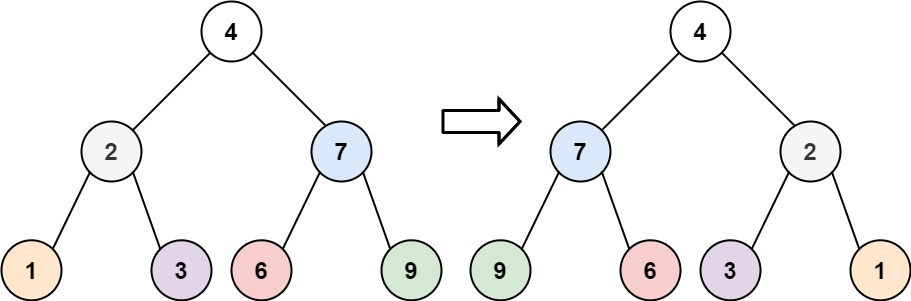
输入：root = [4,2,7,1,3,6,9]

输出：[4,7,2,9,6,3,1]

• 示例 2：

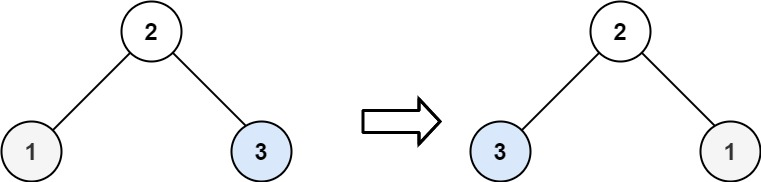
输入：root = [2,1,3]

输出：[2,3,1]

• 示例 3：

输入：root = []

输出：[]

解法1 使用递归翻转二叉树

本题使用递归法非常简单，先处理终止条件（即当前节点为空时），后续只需要对当前节点进行翻转，同时递归对左右子树分别调用翻转即可。具体代码如下：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
       if(root == nullptr) return nullptr; // 如果当前节点为空，则直接返回
       invertTree(root->left); // 对左子树进行翻转
       invertTree(root->right); // 对右子树进行翻转
       swap(root->left, root->right); // 翻转当前节点的左右子节点
       return root; // 返回根节点
    }
};

解法2 层序迭代（广度优先算法）

这题也可以通过修改层序遍历的算法得到，具体代码如下：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root) return root;
        queue<TreeNode*> nodeQue; // 使用队列来进行广度优先遍历
        nodeQue.push(root);
        while(!nodeQue.empty()){
            int size = nodeQue.size();
            for(int i = 0; i < size; i++){
                TreeNode* curNode = nodeQue.front();
                nodeQue.pop();
                swap(curNode->left, curNode->right); // 翻转左右节点
                if(curNode->left)nodeQue.push(curNode->left);
                if(curNode->right)nodeQue.push(curNode->right);
            }
        }
        return root;
    }
};

Leecode 101. 对称二叉树

• 题目链接：https://leetcode.cn/problems/symmetric-tree/description/

题目描述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

• 示例 1：

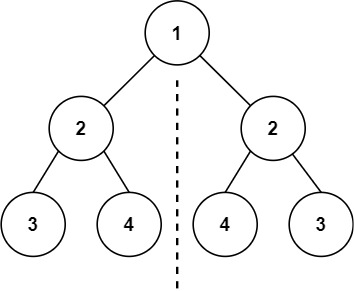
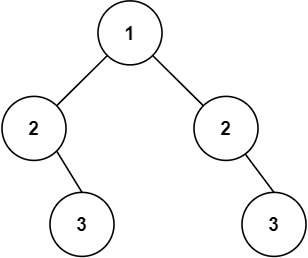
输入：root = [1,2,2,3,4,4,3]

输出：true

• 示例 2：

输入：root = [1,2,2,null,3,null,3]

输出：false

解法1 使用两个栈同时遍历左右子树并比对

首先是自己写出来的代码，通过一步一步分类讨论并进行相应处理。使用两个栈来分别存放两边子树，并逐步弹出镜像对称的节点进行比较。但写完之后就感觉自己用了很多if，应该是由较大代码冗余的。但尽管如此，还是将我自己写的第一版代码进行一下展示。

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root->left && !root->right) return true; // 如果左右两个子树都不存在，相当于只有一个根节点，返回true
        if(!root->left || !root->right) return false; // 如果两个子树有一个存在另一个不存在，直接返回false
        stack<TreeNode*> leftStk; // 该栈用于遍历左子树
        stack<TreeNode*> rightStk; // 该栈用于遍历右子树
        leftStk.push(root->left); // 将左子树的根节点入栈
        rightStk.push(root->right); // 将右子树的根节点入栈
        while(!leftStk.empty() && !rightStk.empty()){ // 如果有一个栈已经为空，则直接结束循环（避免访问空栈造成越界访问）
            TreeNode* leftNode = leftStk.top();  // 左子树中栈顶节点出栈
            leftStk.pop();
            TreeNode* rightNode = rightStk.top(); // 右子树中栈顶节点出栈
            rightStk.pop();
            if(leftNode->val != rightNode->val) return false; // 如果当前节点的值不相等，则返回false
            if((leftNode->left && !rightNode->right) || (!leftNode->left && rightNode->right)) return false; // 如果子节点的存在性不对称，则返回false
            if((leftNode->right&& !rightNode->left) || (!leftNode->right && rightNode->left)) return false;
            if(leftNode->left && rightNode->right) {
                leftStk.push(leftNode->left); // 判断当前两个节点的镜像子节点是否存在，如果存在则需要入栈
                rightStk.push(rightNode->right);
            }
            if(leftNode->right && rightNode->left) {// 判断当前两个节点的另外两个镜像子节点是否存在，如果存在则需要入栈
                leftStk.push(leftNode->right);
                rightStk.push(rightNode->left);
            }
        }
        if(!leftStk.empty() || !rightStk.empty()) return false; // 如果上面循环结束，而有一个栈还未空，说明不对称，返回false
        return true; // 如果经过上面所有检查都通过，最终返回true
    }
};

上面这段代码我自己写完之后都能感觉到，用了太多的if判断，需要采用其他方法来进行优化。

解法2 使用递归实现

接下来考虑使用递归的方式来实现对称的比较，使用一个Helper递归函数来比较根节点的左右子树中的节点是否对称。具体代码如下：

class Solution {
public:
    bool symmetricHelper(TreeNode* leftTreeNode, TreeNode* rightTreeNode){ // 递归辅助函数，用于比较两侧树中的节点是否对称
        if(!leftTreeNode && !rightNode) return true; // 如果此时这两个节点都为空，则说明对称，返回true
        if(!leftTreeNode || !rightNode) return false; // 如果有一个不为空，说明此时一个空一个不空，说明不对称，返回false

        if(leftTreeNode->val != rightTreeNode->val) return false; // 如果两个节点中的值不相等，则也返回false
        bool outsideSym = symmetricHelper(leftTreeNode->left, rightTreeNode->right); // 递归检查左子树的左侧节点与右子树中的右侧节点是否相等，故称为外侧outside
        bool insideSym = symmetricHelper(leftTreeNode->right, rightTreeNode->left); // 递归检查左子树的右侧节点与右子树中的左侧节点是否相等，故称之为内侧inside
        return outsideSym && insideSym; // 只有内侧外侧都满足对称性的时候，才返回true，故这里是用或运算连接
    }

    bool isSymmetric(TreeNode* root) {
        if(root == nullptr) return true; // 如果根节点为空，则直接返回true
        return symmetricHelper(root->left, root->right); // 否则递归判断左右子树是否满足对称性
    }
};

使用递归来写本题就变得简洁多了，上面代码是在看了一遍卡哥的答案之后就自己直接写出来了。感觉用递归实现还是有一定难度，需要多加熟练。

Leecode 104. 二叉树的最大深度

• 题目链接：https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/

题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

• 示例 1：

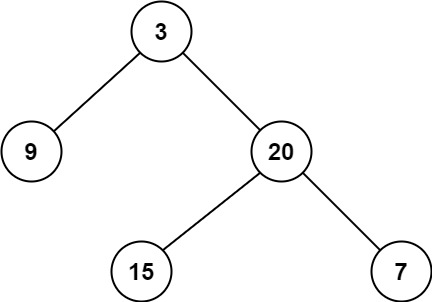
输入：root = [3,9,20,null,null,15,7]

输出：3

• 示例 2：

输入：root = [1,null,2]

输出：2

解法1 广度优先算法

这道题是刚才在层序遍历中已经刷过的题目，这里先直接给出使用修改的层序遍历的最大深度求解代码：

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr) return 0; // 如果根节点为空，则直接返回深度为0
        queue<TreeNode*> nodeQue; // 新建一个队列用于存放节点进行层序遍历
        nodeQue.push(root); // 当根节点先push入队列中
        int depth = 0;
        while(!nodeQue.empty()){
            int size = nodeQue.size();
            depth++; // 只要栈中还有节点，就要将深度+1
            for(int i = 0; i < size; i++){ // 遍历本层每一个节点，将该节点的左右子节点都入队
                TreeNode* curNode = nodeQue.front(); // 当前节点出队
                nodeQue.pop();
                if(curNode->left) nodeQue.push(curNode->left);  // 当前节点的左右子节点（如果有的话）入队列
                if(curNode->right) nodeQue.push(curNode->right);
            }
        }
        return depth;

    }
};

这里相当于是使用了迭代层序遍历的标准模板解法，使用一个队列来入队，同时一层开始的时候的队列长度就是该层中的节点数。只要能够知道这一点那么这类题应该都问题不大了。

解法2 递归法

本题也尝试使用递归法来进行求解，具体代码如下：

class Solution {
public:
    int maxDepthHelper(TreeNode* curNode, int depth){ // 用于递归寻址最大深度
        if(curNode == nullptr) return depth; // 如果当前节点已为空，则直接返回传入的深度
        int leftDep = maxDepthHelper(curNode->left, depth+1); // 否则当前节点不为空，此时递归调用左侧深度，传入的深度为当前节点的深度
        int rightDep = maxDepthHelper(curNode->right, depth+1); // 同时递归调用右侧深度
        return leftDep > rightDep ? leftDep : rightDep; // 返回值为当前节点左右两侧更深的深度，即为要找的最大深度
    }

    int maxDepth(TreeNode* root) {
        return maxDepthHelper(root,0); // 直接调用递归函数，输入初始深度为0
    }
};

上面是使用辅助函数来进行递归，同样也可以采用默认参数的形式进行递归，代码如下：

class Solution {
public:
    int maxDepth(TreeNode* curNode, int depth = 0){ // 默认深度参数为0
        if(curNode == nullptr) return depth; // 如果当前节点为空，则返回当前深度
        int leftDep = maxDepth(curNode->left, depth+1); // 当前节点不为空，查看左侧深度
        int rightDep = maxDepth(curNode->right, depth+1); // 查看右侧深度
        return leftDep > rightDep ? leftDep : rightDep; // 返回左右两侧深度的最大值
    }
};

这里使用默认参数调用可以使得代码看起来更加简洁。

Leecode 111. 二叉树的最小深度

• 题目链接：https://leetcode.cn/problems/minimum-depth-of-binary-tree/description/

题目介绍

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

• 示例 1：

输入：root = [3,9,20,null,null,15,7]

输出：2

• 示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]

输出：5

解法1 广度优先算法

本题也是在上面层序遍历的十道题目中已经出现过，此处先直接给出层序遍历修改后得到代码：

class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> nodeQue;
        if(root == nullptr) return 0;
        nodeQue.push(root);
        int depth = 0; // 记录深度
        while(!nodeQue.empty()){
            int size = nodeQue.size();
            depth++; // 只要队中还有节点，就要将深度+1
            for(int i = 0; i < size; i++){
                TreeNode* curNode = nodeQue.front();
                nodeQue.pop();
                if(curNode->left) nodeQue.push(curNode->left);
                if(curNode->right) nodeQue.push(curNode->right);
                if(curNode->left == nullptr && curNode->right == nullptr) return depth; // 如果遇到叶节点，直接返回当前叶节点的深度
            }
        }
        return depth;
    }
};

使用上面代码即可通过层序遍历的方式求得数的最小深度。

解法2 递归法求最小深度

本题同样也可以使用递归的方法来实现，具体代码如下：

class Solution {
public:
    int minDepthHelper(TreeNode* curNode, int depth){  // 辅助递归函数
        if(!curNode->left && !curNode->right) return depth; // 如果当前节点的左右子节点都为空，则说明找到了要找到叶节点，直接返回当前深度
        if(!curNode->left) return minDepthHelper(curNode->right, depth + 1); // 如果当前左节点为空，则需要继续寻找右节点的最小深度
        if(!curNode->right) return minDepthHelper(curNode->left, depth + 1); // 如果当前右节点为空，继续寻找左节点的最小深度
        int a = minDepthHelper(curNode->left, depth + 1); // 如果左右都不为空，则需要分别查看左右两个节点的最小深度，这一行为左侧最小深度
        int b = minDepthHelper(curNode->right, depth + 1); // 右侧最小深度
        return a < b ? a : b; // 返回左右两个最小深度中更小的一个
    }
    int minDepth(TreeNode* root) {
        if(!root) return 0;  // 如果根节点为空，则直接返回0
        return minDepthHelper(root, 1);  // 如果根节点不为空，则递归到下一层，此时的深度需要+1，故初始值为1
    }
};

同样，上面代码也可以将辅助函数使用默认参数的方式进行替换，可以将代码简化：

class Solution {
public:
    int minDepth(TreeNode* curNode, int depth = 1){ // 初始depth为1是为了方便递归，将深度为0的情况用一个if单独讨论
        if(!curNode) return 0; // 只有初始根节点为空的时候才通过if语句，后续的逻辑能够确保不会递归遍历到空节点。但每一次递归都需要多做一次判断，会带来不必要的计算开销
        if(!curNode->left && !curNode->right) return depth;
        if(!curNode->left) return minDepth(curNode->right, depth + 1);
        if(!curNode->right) return minDepth(curNode->left, depth + 1);
        int a = minDepth(curNode->left, depth + 1);
        int b = minDepth(curNode->right, depth + 1);
        return a < b ? a : b;
    }
};

上面代码从行数上看的确变得更加简洁了，但是实际上每一次递归都会多做一次判断，会造成更多的计算开销。因此针对本题还是更推荐使用辅助函数的方式。

今日总结

今天学习了树的层序遍历相关算法（也即广度优先算法），特别是使用队列来进行层序遍历的范式。今后遇到树相关的题目应当去思考应该通过怎样的遍历方式去访问并修改节点。

另外，今天一连在Leecode上刷了很多道题目，至此已经刷完50道题了，值得小小庆祝一下。