CF207C3 Game with Two Trees

CF207C3 Game with Two Trees

妙到家的树上字符串问题。

约定

• 树 \(1\)：\(t_1\)。

• 树 \(2\)：\(t_2\)。

• \(S_{1/2}(i,l)\) 为树 \(1/2\) 上节点 \(i\) 沿父亲走经过 \(l\)​ 条边所构成的字符串。

• \(E_{1/2}(u,v)\) 为树 \(1/2\) 上，连接节点 \(u,v\)​ 的边的字符。

• \(fa_{1/2}u\) 为树 \(1/2\) 上 \(u\) 的父亲。

前置

• Tire 树
• 字符串哈希
• 树上倍增
• 树链剖分

思路

part 1：寻找对应点

我们先把树 \(1\) 建成一棵 Tire 树，把树 \(2\) 建成一棵正常的树。

我们对于每个树 \(2\) 上的点 \(u\) 寻找一个第一颗树上的点 \(i\)（\(l\) 为 \(i\) 的深度，根深度为 \(0\)），满足：

• \(S_1(i,l)=S_2(u,i)\)。
• \(l\) 最大。

两个条件必须都满足，由于树 \(1\) 是一棵 Tire 树，所以 \(i\) 是唯一存在的，我们把这样的 \(i\) 称为对应点。

我们可以枚举树 \(2\) 的节点 \(u\)，节点 \(i\) 从树 \(1\) 的根开始，如果 \(i\) 的儿子 \(v\) 使得 \(E_2(u,fa_2u)=E_1(rt,v)\)，那么我们把 \(u\) 向上走，把 \(i\) 走向 \(i\) 的儿子 \(v\)。

这样可以暴力的找到我们需要的点。

但是肯定也会获得 TLE 的好成绩

我们考虑优化这个过程，可以树上的做字符串 hash 判断某一段链（从祖先到子孙）是否相等，现在要解决的问题是怎么速的爬树（寻找点）。

首先 \(u\) 是向上跳，我们可以想到倍增，但 \(i\) 需要向下，怎么解决呢？

其实 \(i\) 的主要问题在于需要判断下一条边是否有需要的边，我们可以对树 \(1\) 进行树链剖分，这样子每次肯定是向下走一条链，确定了 \(i\) 的方向。

然后枚举 \(k\)（\(k\) 从大到小，且 \(2^k\) 小于 \(i\) 所在重链向下的长度）表示 \(u\) 向上爬 \(2^k\) 个点，\(i\) 向下跳 \(2^k\) 个点，然后判断跳的这一段边的字符串是否相等，相等就跳过去。

如果 \(1\) 个节点都跳不了，那么我们就手动判断 \(i\) 是否可以向下，如果可以，就向下；如果不行，则 \(i\) 点以是最优选择。

分析一下这里的复杂度，如果可以沿着重链向下跳，那么这条重链最多跳 \(\log n\) 次。跳完重链或者重链无法向下以后，跳一条轻边，而根据树剖的性质，最多跳 \(\log n\) 条轻边，也就是最多换 \(\log n\) 条重链。

总时间复杂度 \(\log^2 n\)。

inline int fr(int u,int v,int s)//树 1 点 u；树 2 点 v
{
    for(int i=lg[min(len[v],dep[u])];~i;i--)
        if((h[s]-h[fa[u][i]]+mod)%mod==val[id[dfn[v]+(1<<i)]]*base[dep[fa[u][i]]]%mod)//沿重链跳
            u=fa[u][i],v=id[dfn[v]+(1<<i)];
    if(u==1||!tr[v][to[u]]) return v;//判断有没有轻边可以跳
    return fr(fa[u][0],tr[v][to[u]],s);//跳轻边
}

这里树 \(1\) 是 Tire 树进行了树剖，树 \(2\) 是正常树进行了倍增。

part 2 反馈询问

求得了上面的对应点，我们要怎样利用对应点去求答案呢？

part 2.1 树 2 加入点

假设这个是树 \(1\)。

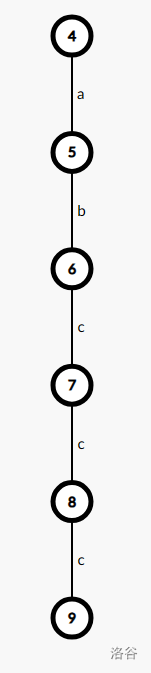
这个是树 \(2\)。

现在树 \(2\) 的 \(9\) 号节点的对于点是树 \(1\) 的 \(6\) 号节点。

我们有 \(S_1(6,5)=abccc\)，有 \(S_2(9,5)=cccba\)。

假设其余节点已经加入，现在加入的节点是 \(9\) 号节点。

那么 \(9\) 号节点在树 \(1\) 上的答案可以是 \(1、2、3、4、5、6\) 号节点共 \(6\) 个。

不难发现树 \(1\) 上对于点所在的到根的链上的任意一个点都可以成为 \(9\) 号点的答案。

也很好证明，因为树 \(1\) 从上到下需要匹配树 \(2\) 从下到上，那么树 \(1\) 到对应点的每一个前缀，都是树 \(2\) 向上爬的后缀。

但有些时候，树 \(1\) 上的对应点可能还没有加入，所以我们对于树 \(1\) 我们需要动态的维护一条链上的点是否加入。

这里可以搭配 dfn 序食用树状数组，每次插入一个树 \(1\)​ 的节点，我们对于它子树这一个 dfn 序区间整体加 1，查询直接单点查询该点的值，是不是动态维护出了一条链上的节点。

part 2.2 树 1 加入节点

这个会稍微复杂一点点，我们还是先画个图：

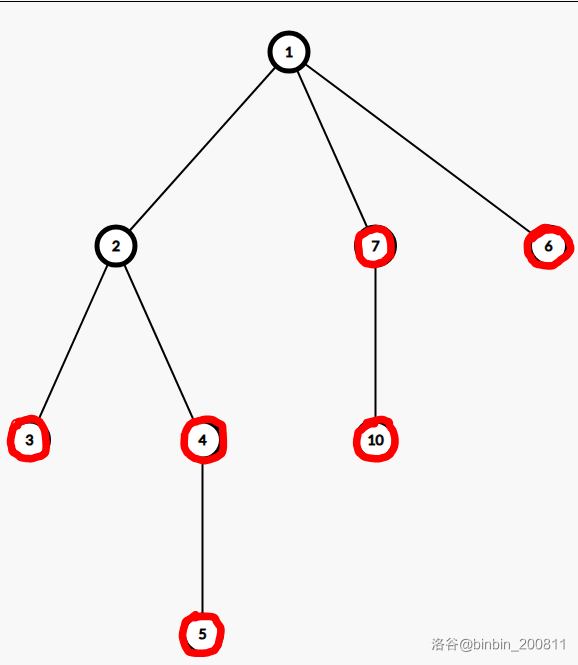
这棵树是树 \(1\)，圈住的红色点还没有加入。

至于边上的字母呢？这不重要

假设图中蓝色的节点是被树 \(2\) 上的节点定为对应点。

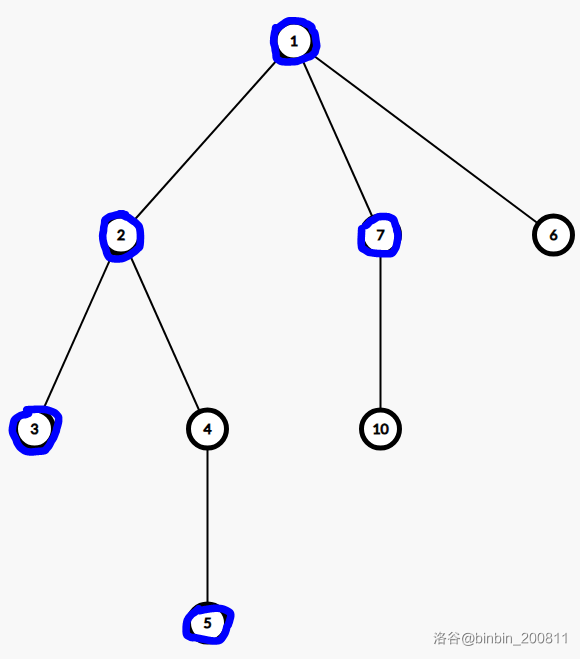
你说这种对应不可能？对不起，这也不重要

假设我们现在插入了树 \(1\) 中的 \(2\) 号节点，那么所有在 \(2\) 号节点的子树内，被树 \(2\) 对应的次数就是 \(2\) 号节点答案。

分析和 part 2.1 朴素情况下的分析一致。

每次树 \(2\) 中插入一个节点，我们就向树 \(1\) 对应点 dfn 序的位置加 \(1\)​，每次查询区间查询子树即可。

这个就是单点修改区间查询。

还是可以食用树状数组。

//T1 树 2 查询使用的；T2 是树 1 查询使用的
	b[1]=1;for(int i=2;i<=n2;i++) b[i]=fr(i,1,i);//求对应点
    T1.updata(dfn[1],1),T1.updata(dfn[1]+siz[1],-1);//区间加
    T2.updata(dfn[b[1]],1);//单点加
	ans=1;//两个 1 号节点互相匹配，答案为 1
    for(int i=1,x=1,y=1;i<=m;i++)
    {
        if(op[i]==1)//加入树 1 点
        {
            int u=a[++x];//a 为 Tire 树上点编号
            ans+=T2.getsum(dfn[u]+siz[u]-1)-T2.getsum(dfn[u]-1);
            T1.updata(dfn[u],1),T1.updata(dfn[u]+siz[u],-1);
        }
        else//加入树 2 点
        {
            int u=b[++y];//b 为对应点编号
            ans+=T1.getsum(dfn[u]);
            T2.updata(dfn[u],1);
        }
        printf("%lld\n",ans);
    }

如果看不懂树状数组的话，也可以手搓线段树。

CODE

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define N 3e5
#define mod 998244353

const int maxn=3e5+5;

inline int read() {
    int s = 0, w = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            w = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
    return s * w;
}

struct treearray
{
    int tree[maxn];
    inline int lowbit(int x){return x&(-x);}
    inline void updata(int x,int y){for(;x<=N;x+=lowbit(x)) tree[x]+=y;}
    inline int getsum(int x){int sum=0;for(;x;x-=lowbit(x)) sum+=tree[x];return sum;}
}T1,T2;

int n1,n2,m;
int a[maxn],b[maxn];

int idx;
int tr[maxn][27],siz[maxn],hso[maxn],dfn[maxn],id[maxn],len[maxn];
int op[maxn*2],to[maxn],fa[maxn][20],dep[maxn];

int lg[maxn*2];
ll base[maxn*2],h[maxn],val[maxn];

ll ans;

inline void dfs1(int u)
{
    siz[u]=1;
    for(int i=0;i<26;i++)
    {
        int v=tr[u][i];
        if(!v) continue;
        val[v]=(131*val[u]+i+47)%mod;
        dfs1(v);
        siz[u]+=siz[v];
        if(siz[v]>siz[hso[u]]) hso[u]=v;
    }
}
inline void dfs2(int u)
{
    dfn[u]=++idx;id[idx]=u;
    if(!hso[u]) return;
    dfs2(hso[u]);len[u]=len[hso[u]]+1;
    for(int i=0;i<26;i++)
    {
        int v=tr[u][i];
        if(!v||v==hso[u]) continue;
        dfs2(v);
    }
}
inline int fr(int u,int v,int s)
{
    for(int i=lg[min(len[v],dep[u])];~i;i--)
        if((h[s]-h[fa[u][i]]+mod)%mod==val[id[dfn[v]+(1<<i)]]*base[dep[fa[u][i]]]%mod)
            u=fa[u][i],v=id[dfn[v]+(1<<i)];
    if(u==1||!tr[v][to[u]]) return v;
    return fr(fa[u][0],tr[v][to[u]],s);
}

int main()
{
    // freopen("20.in","r",stdin);
    // freopen("droot.out","w",stdout);
    // scanf("%d",&m);
    m=read();
    n1=n2=1;dep[1]=a[1]=1;
    base[0]=1;for(int i=1;i<=m;i++) base[i]=base[i-1]*131%mod;
    for(int i=1;i<=m;i++)
    {
        char c;int u;
        // scanf("%d%d",&op[i],&u);
        op[i]=read(),u=read();
        while(1){c=getchar();if('a'<=c&&c<='z') break;}
        if(op[i]==1)
        {
            n1++;
            if(!tr[a[u]][c-'a']) tr[a[u]][c-'a']=n1;
            a[n1]=tr[a[u]][c-'a'];
        }
        else
        {
            n2++;
            dep[n2]=dep[u]+1;fa[n2][0]=u;to[n2]=c-'a';
            h[n2]=(h[u]+(47ll+to[n2])*base[dep[u]])%mod;
        }
    }
    dfs1(1);dfs2(1);
    lg[0]=-1;for(int i=2;i<=m;i++) lg[i]=lg[i>>1]+1;
    for(int j=1;j<=lg[n2];j++) for(int i=1;i<=n2;i++) fa[i][j]=fa[fa[i][j-1]][j-1];
    b[1]=1;for(int i=2;i<=n2;i++) b[i]=fr(i,1,i);
    T1.updata(dfn[1],1),T1.updata(dfn[1]+siz[1],-1);
    T2.updata(dfn[b[1]],1); ans=1;
    for(int i=1,x=1,y=1;i<=m;i++)
    {
        if(op[i]==1)
        {
            int u=a[++x];
            ans+=T2.getsum(dfn[u]+siz[u]-1)-T2.getsum(dfn[u]-1);
            T1.updata(dfn[u],1),T1.updata(dfn[u]+siz[u],-1);
        }
        else
        {
            int u=b[++y];
            ans+=T1.getsum(dfn[u]);
            T2.updata(dfn[u],1);
        }
        printf("%lld\n",ans);
    }
}

最后代码就懒得注释喽。

后记

实际上如果要做出这题，更多时候应该是先想：

1. 要怎么求答案——》对应点
2. 对应点要怎么求——》树剖加倍增

还是一道很有启发性的题目。