Moving Average

移动平均算法Demo

#!/usr/bin/python2.7
# Fetch data from BD and analyse.

import json
import urllib
import traceback
import numpy as np
# import pandas as pd
import matplotlib.pyplot as plt
#from scipy import stats

def fetch_raw_data(url):
    try:
        response = urllib.urlopen(url).read().decode('utf-8')
        return json.loads(response)
    except Exception, e:
        err = traceback.format_exc()
        print("fetch_raw_data err: {}".format(err))

# 移动平均算法
def moving_average(f_t):
    if type(f_t) is not np.ndarray:
        raise TypeError\
            ('Expected one dimensional numpy array.')
    if f_t.shape[1] != 1:
        raise IndexError\
            ('Expected one dimensional numpy array, %d dimensions given.' % (f_t.shape[1]))

    f_t = f_t.flatten()
    window = 5
    mode = 'same'
    g_t = np.ones(int(window))/float(window)
    # Deal with boundaries with atleast lag/2 day window
    # ma = np.convolve(f_t,g_t,mode)
    # ma = np.convolve(f_t,g_t,mode)[window-1:-window+1]
    ma = np.convolve(f_t,g_t)[window-1:-window+1]
    return ma

def raw_data():
    start_ts = 1533204000
    stop_ts = 1533222000
    url = 'http://8.8.8.8/path/data?begin_time={}&end_time={}&type=asia'
    url = url.format(start_ts,stop_ts)
    result = fetch_raw_data(url)
    # downloadspeed_lst = result['result']['downloadspeed']
    downloadspeed_lst = result['result']['totaluploadspeed']
    downloadspeed_lst = [ [ele,] for ele in downloadspeed_lst ]
    return downloadspeed_lst

def run(downloadspeed_lst):
    downloadspeed_ndarray = np.array(downloadspeed_lst)
    ma = moving_average(downloadspeed_ndarray)
    return ma

data = raw_data()
ma = run(data)
t = np.arange(4, len(data))
plt.plot(t, data[4:], lw=1.0)
plt.plot(t, ma, lw=1.0)
plt.show()

执行结果：

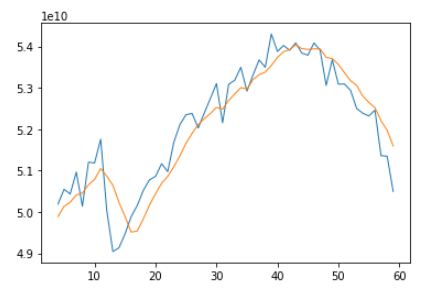
蓝色是原始数据，棕色是经过移动平均算法弱化后的数据。

2018-08-07 补充

import numpy as np
from matplotlib import pyplot as plt

def moving_average(array, window=3):
    N = window
    n=np.ones(N)
    weights=n/N
    sma=np.convolve(weights,array)[N-1:-N+1]

    t=np.arange(N-1,len(array))
    plt.plot(t,array[N-1:],lw=1)
    plt.plot(t,sma,lw=2)
    plt.show()
    return sma

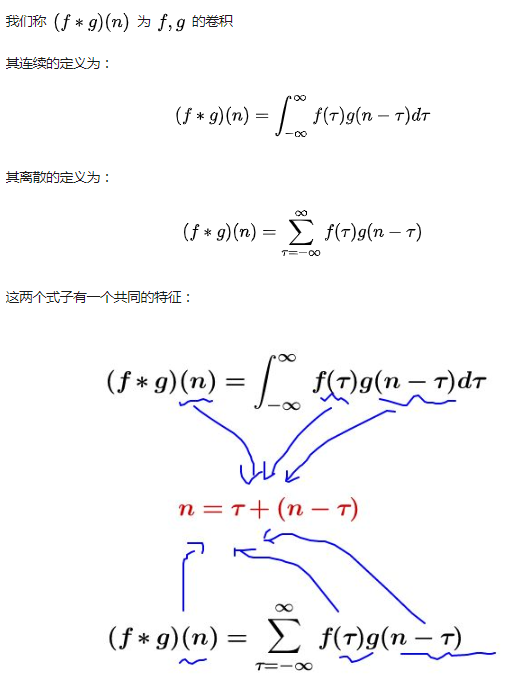
卷积运算

numpy.convolve(weights,array)[N-1:-N+1]

weight = [a,b,c]
array = [i,j,k,m,n]

Result：
[ai, bi+aj, ci+bj+ak, cj+bk+am, ck+bm+an, cm+bn, cn][N-1:-N+1]

如何理解卷积运算？

参考：https://www.cnblogs.com/21207-iHome/p/6231607.html

参考：https://docs.scipy.org/doc/numpy/reference/generated/numpy.convolve.html