线性分类 Linear Classification

软分类：y 的取值只有正负两个离散值，例如 {0, 1}

硬分类：y 是正负两类区间中的连续值，例如 [0, 1]

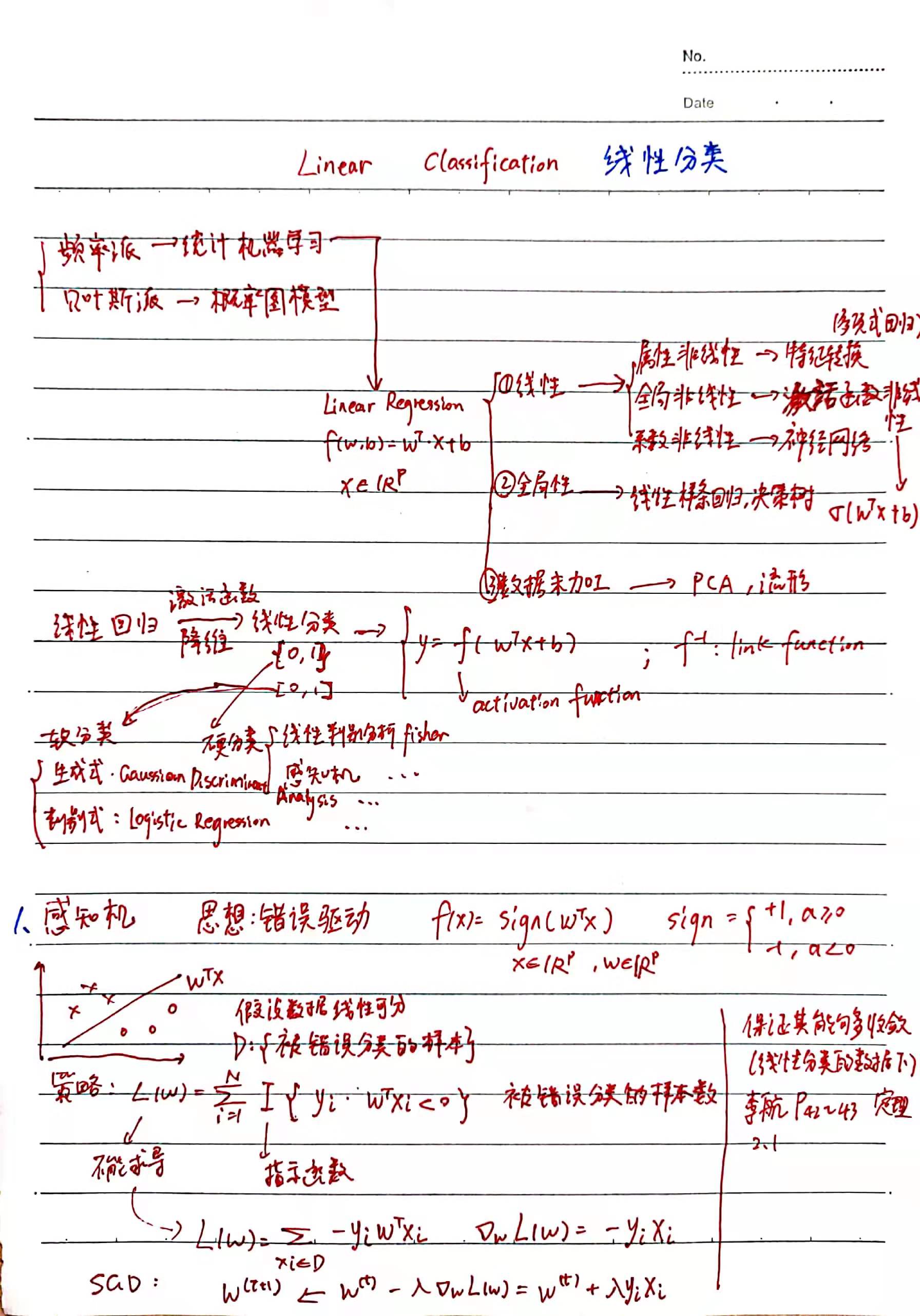
一、感知机

主要思想：分错的样本数越少越好

用指示函数统计分错的样本数作为损失函数，不可微；

对错误分类样本，∑ -y_i * f(x_i) = ∑ -y_i * W^Tx_i  (因为求和项一定大于0，所以损失函数越小表示错误分类的样本越少)

二、线性判别分析

主要思想：同一类别的样本方差足够小，不同类别之间分散开（类内小，类间大）

Rayleigh quotient 和 generalized Rayleigh quotient

函数 R(A, x) = x^HAx / x^Hx ，其中 A 是 Hermitan矩阵，如果是实矩阵则满足 A^T = A。

性质：λ_min  <= R(A, x) <= λ_max   ，即最大值为 A 的最大特征值、最小值为 A 的最小特征值

函数 R(A, B, x) = x^HAx / x^HBx ，其中 A、B 是 Hermitan矩阵，B 正定。

令 x = B^-1/2x'，由瑞利商性质可知，R(A, B, x) 的最大值是 B^-1/2AB^-1/2 （或者 B^-1A）的最大特征值，最小值是其最小特征值

与 LDA 的关系：

二类：

　　数据是 p 维，只有两个类别，经过 LDA 投影到投影到一条直线，投影直线为向量 w（只关心其方向，设为单位向量即可），样本点x_i 在直线上的投影为z_i = w^Tx_i ，记类别 1 和类别 2 两个集合为c1、c2，对 p 维数据 x 两个集合的样本均值和方差分别为 μ_c1 、 μ_c2 、S_c1 、S_c2

　　样本点投影到直线后有样本均值 z_k拔 和样本方差 S_k

　　LDA 目标函数的定义要让类内方差小类间方差大，则

　　J(W) = (z₁拔 - z₂拔 )² / (S₁ + S₂)  

　　　　 = w^T (μ_c1 - μ_c2)(μ_c1 - μ_c2)^Tw /  w^T (S_c1 + S_c2) w

　　　　 = w^T S_b w /  w^T S_w w

　　这个目标函数的 argmax 可以对其求导后令导数为零，得到向量 w 正比于 Sw^-1(μ_c1 - μ_c2)。也可以直接利用瑞利商的结论，最大值为 Sw^-1Sb 的最大特征值，二分类时 S_b w 的方向恒为 μ_c1 - μ_c2 （因为(μ_c1 - μ_c2)^Tw 结果是 scalar），令 S_b w  = λ (μ_c1 - μ_c2) ，代入 (Sw^-1Sb)w = λw，得到 w = Sw^-1(μ_c1 - μ_c2) 结果一样。

多类：　　

　　数据是 p 维，有 K 个类别，经过 LDA 投影到低维（q 维）平面，基为（w₁，w₂，...，w_q），共同构成矩阵W_pxq

　　J(W) = W^T S_b W / W^T Sw W，类间方差 S_b = Σ Nj (μ_cj - μ)(μ_cj - μ)^T ，for j = 1, 2, ..., K；类内方差 Sw =  Σ Σ (x_i - μ_cj)(x_i - μ_cj)^T for j = 1, 2, ..., K  and every x_i in c_i

　　为了应用瑞利商结论，分子分母都各自求主对角线元素乘积，J(W) = ∏ w_i^T S_b w_i / w_i^T Sw w_i ，for i = 1, 2, ..., q 。目标函数的最大值为 Sw^-1Sb 最大的q个特征值的乘积，W 就由这 q 个最大特征值对应的特征向量组成。

　　注意降到的维度 q 最大为 K-1。（因为知道了前K-1个 μ_cj 后最后一个μ_cj 可以由前K-1个表示）

监督降维：根据以上分析，对 x_i 就可以进行降维 z_i = W^Tx_i

分类：LDA 用来分类的思路，假设各个类别的数据符合各自的高斯分布，LDA 投影后用 MLE 计算各个类别的均值和方差，就得到了各个类别服从高斯的概率密度函数。对于一个新样本，将其投影后的向量代入各类的分布计算一下概率，最大的就是样本所属的类。

三、Logistic 回归

判别模型，直接用一个函数拟合，计算后验概率 P(y|x)。直接用 MLE 来估计参数 W / 用梯度下降优化求参数 W 。

为什么不能用均方误差作为logistic regression的损失函数？——均方误差不能准确衡量分类效果的好坏

如果用的话，考虑两种情况

1. label 是1，而 f(x) = 0，那其实现在距离目标很远，但是微分值却是0，

2. label是0，但是 f(x) =1，微分算出来也是0，也不对，原因就出在sigmoid函数求导之后会出现 f(x) * (1-f(x))。

所以，这并不符合实际，距离优化目标远的情况微分值却很小，用均方误差是很难优化到一个好的结果。

 

logistic regression 再如何改进？—— cascading logistic regression models  神经网络

看一下 logistic regression 和 linear regression 中的梯度：

sigmoid函数怎么来的？——高斯判别分析

四、高斯判别分析：

生成模型，不对条件概率 P(y | x) 直接建模，引入 P(y) 的先验分布。

根据贝叶斯定理（执果索因）：P(y | x) = P(x | y)P(y) / P(x)，也即 P(y=c_k | x_i) 正比于 P(x_i | y=c_k) P(y=c_k)，分别对这两部分建模后，对于一个新样本计算P(y=c_k | x_i)，概率最大的c_k 就是样本所属的类别。

以二分类为例，对先验 P(y=c_k) 建模最直觉的想法就是遍历所有训练数据，计算 P(y=c_k) = N_k / N 。这个结果其实也就来源于，假设 Y 服从参数为 p 的伯努利分布，通过 MLE 进行参数估计。

对似然 P(x | y=c_k) 的估计呢？——对每个类别都假设 P(x | y=c_k) 服从均值为 μ_k 、方差为 Σ_k 的高斯分布就好了。

P(x | y=c_k) = ∏ P(x_i | y=c_k) ，for every x_i in c_k ，MLE 估计所有的 μ_k 和 Σ_k 。

结果比较差，怎么改进？ ——不同类别的高斯分布共享同一个 Σ，减少参数改善过拟合。

可以看出，高斯判别分析认为输入的各个维度特征之间存在相关性。

能不能和 sigmoid 函数联系起来？

先看一个后验概率表达式，把分子除下去就看到熟悉的 σ (z) 形式了，可以发现 sigmoid 函数的作用就是把 logit 压到 probability。

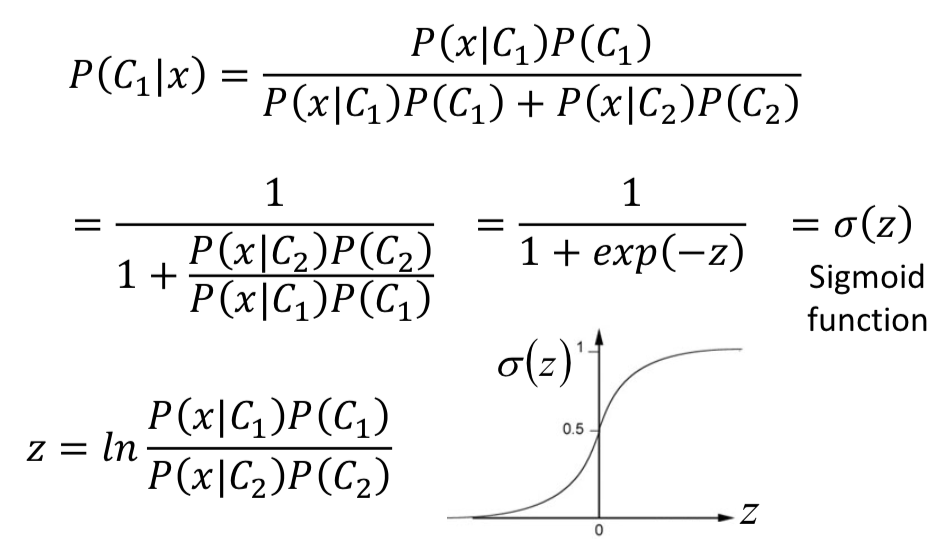
另一个结论：似然设为服从高斯分布，且不同类别的高斯分布共享方差矩阵的情况下，高斯判别分析：

那为什么不直接去找 W 和 b 呢？ ——logistic regression

概率判别模型和概率生成模型的一点比较分析：

为什么 discriminative model 要比generative model的效果要好？—— 先验等假设限制了生成模型效果，但并不是所有情况下都更好。

因为generative model 做了一些假设，比如是高斯分布，伯努利分布，是不是朴素贝叶斯（假定不同维度是独立的）。

所以：

　　1. 训练集比较小的时候，这些“脑补”反而可能会更有效，这时候discriminative model就会受数据的影响更大。

　　2. 同理 generative model 对数据噪声也不太敏感。

　　3. Priors and class-dependent probabilities（先验和似然）可以从不同的来源去估计。

 

五、朴素贝叶斯

服从条件独立性假设

后验概率最大化 等价于 期望风险最小化