NumPy数据的归一化

数据的归一化

首先我们来看看归一化的概念:

数据的标准化（normalization）和归一化

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。

目前数据标准化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据标准化方法的选择上，还没有通用的法则可以遵循。

归一化的目标

1 把数变为（0，1）之间的小数
主要是为了数据处理方便提出来的，把数据映射到0～1范围之内处理，更加便捷快速，应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式
归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量。比如，复数阻抗可以归一化书写：Z = R + jωL = R(1 + jωL/R) ，复数部分变成了纯数量了，没有量纲。
另外，微波之中也就是电路分析、信号系统、电磁波传输等，有很多运算都可以如此处理，既保证了运算的便捷，又能凸现出物理量的本质含义。

归一化后有两个好处

1. 提升模型的收敛速度

如下图，x₁的取值为0-2000，而x₂的取值为1-5，假如只有这两个特征，对其进行优化时，会得到一个窄长的椭圆形，导致在梯度下降时，梯度的方向为垂直等高线的方向而走之字形路线，这样会使迭代很慢，相比之下，右图的迭代就会很快（理解：也就是步长走多走少方向总是对的，不会走偏）

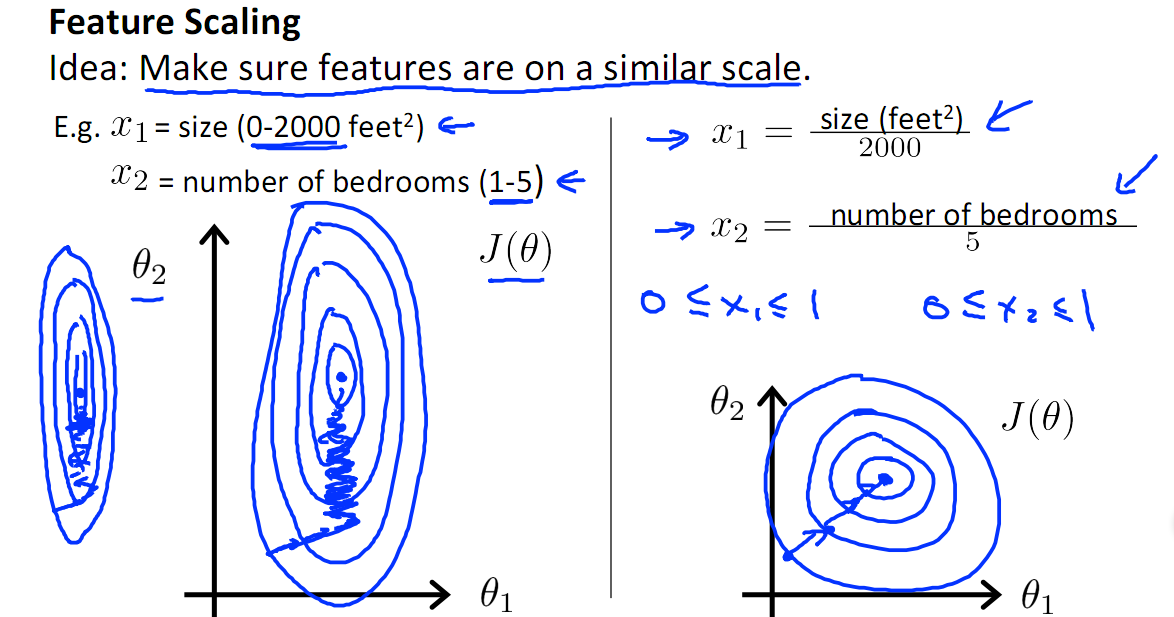
2.提升模型的精度

归一化的另一好处是提高精度，这在涉及到一些距离计算的算法时效果显著，比如算法要计算欧氏距离，上图中x2的取值范围比较小，涉及到距离计算时其对结果的影响远比x1带来的小，所以这就会造成精度的损失。所以归一化很有必要，他可以让各个特征对结果做出的贡献相同。

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行标准化处理。

在数据分析之前，我们通常需要先将数据标准化（normalization），利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。

从经验上说，归一化是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。

现在我们再来看看基础的NumPy代码是如何实现的：

>>> x=np.random.random((,))

>>> x

array([[0.44951388, 0.58974524, 0.43980589],

       [0.3082853 , 0.71042825, 0.02617535],

       [0.10836115, 0.66774964, 0.85824697],

       [0.01442332, 0.76459011, 0.75151452],

       [0.64054078, 0.02121539, 0.87271819],

       [0.75971598, 0.4268253 , 0.66039724],

       [0.11865255, 0.14679259, 0.53782096],

       [0.85085254, 0.26284603, 0.00246512],

       [0.41957758, 0.96842006, 0.65555725],

       [0.70227785, 0.78120928, 0.54771033]])

>>> x.mean()

array([0.43722009, 0.53398219, 0.53524118])

>>> xc=x-x.mean()

>>> xc

array([[ 0.01229379,  0.05576305, -0.0954353 ],

       [-0.1289348 ,  0.17644606, -0.50906583],

       [-0.32885894,  0.13376745,  0.32300579],

       [-0.42279677,  0.23060792,  0.21627333],

       [ 0.20332068, -0.5127668 ,  0.33747701],

       [ 0.32249589, -0.10715689,  0.12515606],

       [-0.31856754, -0.3871896 ,  0.00257978],

       [ 0.41363245, -0.27113616, -0.53277606],

       [-0.01764252,  0.43443787,  0.12031607],

       [ 0.26505776,  0.24722709,  0.01246915]])

>>> xc.mean()

array([ 5.55111512e-18,  3.33066907e-17, -4.44089210e-17])

因为最后归一化的均值在0附近，因此在机器精度范围之内，该均值为0。