yzoj P2343 & 洛谷 P1437 [HNOI2004]敲砖块

题意

在一个凹槽中放置了N层砖块，最上面的一层油N块砖，从上到下每层一次减少一块砖。每块砖都有一个分值，敲掉这块砖就能得到相应的分值，如图所示。

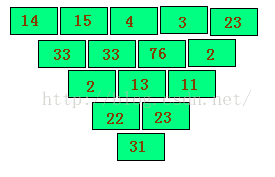
如果你想敲掉第i层的第j块砖的话，若i=1，你可以直接敲掉它；若i>1，则你必须先敲掉第i-1层的第j和第j+1块砖。

你现在可以敲掉最多M块砖，求得分最多能有多少。

一道dp题,一开始想到的是一行一行dp然而发现,选[ i , j ]就要选[ i-1 , j+1]和[ i ,j ]上面所有的方块，似乎不满足无后效性,那怎么办呢？

我们发现输入文件时这样的

4 5
2 2 3 4
8 2 7
2 3
49

我们可以去思考是不是可以一列一列dp，从n列向1列dp这样就没有后效性了，我们可以定义状态f[i][j][k]表示当前在第i列选了j个，总共选了k个，状态转移方程为

f[i][j][k]=max(f[i+1][t][k-j]+s[i][j],f[i][j][k])

t>=j-1&&t<=n-i

s[i][j]表示第j列前i个的和

代码

#include<bits/stdc++.h>
using namespace std;
int n,m,ans,f[55][55][3000],a[55][55],s[55][55];
int main(){
	scanf("%d %d",&n,&m);
	memset(f,-0x3f,sizeof(f));
    f[n+1][0][0]=0;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n-i+1;++j){
			scanf("%d",&a[i][j]);
		}
	}
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n-i+1;++j){
			s[j][i]=s[j][i-1]+a[i][j];
		}
	}
	for(int i=n;i>=1;--i){
		for(int j=0;j<=n-i+1;++j){
			for(int k=j;k<=m;++k){
				for(int t=max(j-1,0);t<=n-i;++t){
					f[i][j][k]=max(f[i+1][t][k-j]+s[i][j],f[i][j][k]);
				}
			}
		}
	}
    for(int i=1;i<=n;++i){
    	for(int j=1;j<=n-i+1;++j){
    		ans=max(ans,f[i][j][m]);
    	}
    }
    printf("%d",ans);
	return 0;
}