web项目脱敏白名单管理

写在前面

下午没事, 看一下同事写的脱敏白名单管理功能. 所谓的脱敏就是将页面中查询出的信息列表当中的身份证号及手机号等关键信息部分用*号代替.该功能主要思路是新增一个页面用于配置哪些页面以及页面中哪些字段需要加入脱敏管理. 不上图的穷b叨叨就是耍流氓.

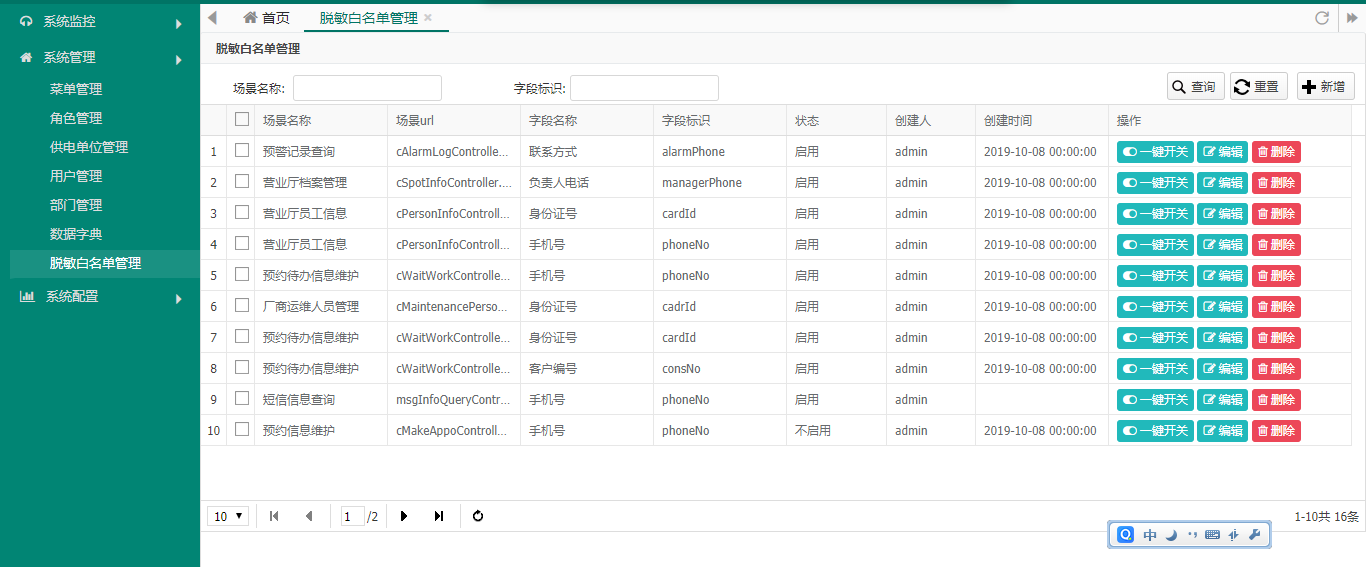
以手机号为例, 大致思路就是在需要脱敏显示关键信息的页面初始化时判断该页面的手机号是否启用了脱敏, 如果启用了则将手机号的值中间5位用*号代替. 未启用则正常显示.

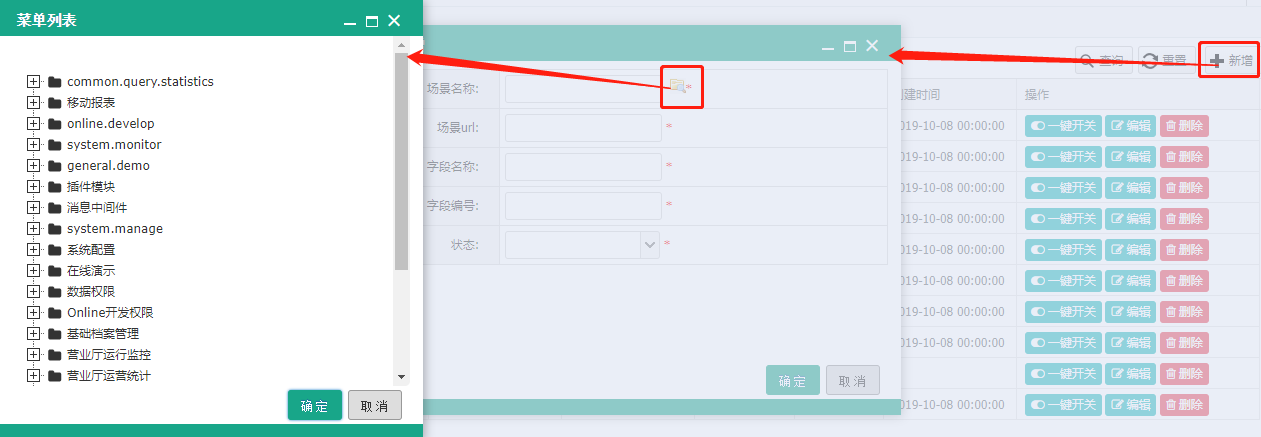
关键步骤(基于jeecg开发平台3.7版本,formatterjs是自定义js方法)

1.jsp

引入判断是否启用脱敏的js, 页面初始化的执行方法

js部分

    var phoneNoFlag;
    $(function () {
        //检查手机号是否脱敏
        phoneNoFlag = isTuoMin('managerPhone','cEquipmentInfoController',false);
    });

    //手机号码脱敏显示
    function changePhNoStyle(value, row, index) {
        var phNoLen = value.length;
        if (phNoLen != 11) {
            return value;//格式不准确，不脱敏
        } else {
            if (phoneNoFlag) {
                return value.substr(0, 3) + "*****" + value.substr(8, 3);
            }
            return value;
        }
    }

2.引入的js文件

用于判断字段是否启用了脱敏

/**
 * 查询某菜单某字段是否要求脱敏
 * @author wangzhuang
 * @date 2019/10/08
 * @param fieldNo 字段名
 * @param url 菜单url 格式如：whiteListController
 * @returns
 */
function isTuoMin(fieldNo,url,flag){
         $.ajax({
             type: "post",
             url: "whiteListController.do?checkIsTuoMin",
             data: {
                 fieldNo: fieldNo,
                 url:url
             },
             async : false,//异步请求
             dataType: "json",
             success: function (data) {
                  if (data.success) {
                     flag = true;
                 }
             }
         });
         return flag;
    }

3.后台判断

    /**
     * 检查是否要求脱敏
     *
     * @param request
     * @return
     */
    @RequestMapping(params = "checkIsTuoMin")
    @ResponseBody
    public AjaxJson checkIsTuoMin(HttpServletRequest request) {
        AjaxJson j = new AjaxJson();
        String url = request.getParameter("url");
        String fieldNo = request.getParameter("fieldNo");
        if (whiteListService.queryFlag(url, fieldNo)) {
            j.setSuccess(true);
        } else {
            j.setSuccess(false);
        }
        return j;
    }

功能本身思路简单感觉没什么亮点, 唯一想深入看的就数zTree了, 自从毕业只是ctrl+c ctrl+v, 今天详细看一下zTree.https://www.cnblogs.com/yadongliang/p/11642931.html