POJ 1458 Common Subsequence（最长公共子序列）

题目链接
Time Limit: 1000MS              Memory Limit: 10000K
Total Submissions:         Accepted: 

Description

A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = < x1, x2, ..., xm > another sequence Z = < z1, z2, ..., zk > is a subsequence of X if there exists a strictly increasing sequence < i1, i2, ..., ik > of indices of X such that for all j = 1,2,...,k, x_ij = zj. For example, Z = < a, b, f, c > is a subsequence of X = < a, b, c, f, b, c > with index sequence < 1, 2, 4, 6 >. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.

Input

The program input is from the std input. Each data set in the input contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct.

Output

For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.

Sample Input

abcfbc         abfcab
programming    contest
abcd           mnp

Sample Output

中文题目：

给出两个字符串，求出这样一个最长的公共子序列的长度——子序列的每个字符都能在两个原串中找到，且每个字符的先后顺序和原串中的先后顺序一致。

解题思路：

步骤1-找子问题：将原问题可以分解为求s1左边i个字符的子串和s2左边j个字符子串的最长公共子序列。

步骤2-确定状态：MaxLen(i,j)表示上述最长公共子序列的长度，即为本题的状态。

步骤3-确定状态转移方程：

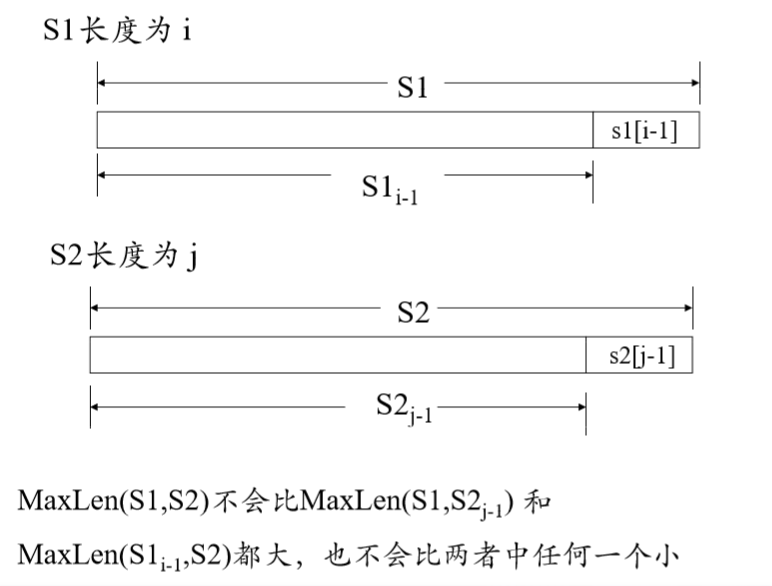
• MaxLen(n,0)=0, MaxLen(0,m)=0 (n=0,1,2...len1, m=1,2...len2)
• if(s1[i-1]==s2[j-1]) MaxLen(i,j) = MaxLen(i-1,j-1)+1;
• else MaxLen(i,j) = Max(MaxLen(i,j-1), ManLen(i-1,j));

重点在于状态转移方程的书写，这一题讲义PPT中画的图很好，言简意赅，我一开始想的是计算s2中以xk为终点的字串在s1中的公共子序列，但是发现自己对题意的理解有误，子串中的各字母是可以隔开的，因此逐个字符比较是最好的。既然是逐个字符相比较，那么自然也要考虑s1的位置。

AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

char s1[];
char s2[];
int maxLen[][];

int main()
{
    while (cin >> s1 >> s2)
    {
        int length1 = strlen(s1);
        int length2 = strlen(s2);
        for (int i = ; i <= length1; i++)
            maxLen[i][] = ;
        for (int j = ; j <= length2; j++)
            maxLen[][j] = ;
        for (int i = ; i <= length1; i++)
        {
            for (int j = ; j <= length2; j++)
            {
                if (s1[i - ] == s2[j - ])
                    maxLen[i][j] = maxLen[i - ][j - ] + ;
                else
                    maxLen[i][j] = max(maxLen[i - ][j], maxLen[i][j - ]);
            }
        }
        cout << maxLen[length1][length2] << endl;
    }
    return ;
}

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int N = ;
char s1[N], s2[N];
int l1, l2;
int dp[N][N];

int DP()
{
    memset(dp, , sizeof(dp));
    for (int i = ; i <= l1; i++)
    {
        for (int j = ; j <= l2; j++)
        {
            if (s1[i-] == s2[j-])dp[i][j] = dp[i - ][j - ] + ;
            else dp[i][j] = max(dp[i - ][j], dp[i][j - ]);
        }
    }
    return dp[l1][l2];
}

int main()
{
    while (scanf("%s%s", s1, s2) != EOF)
    {
        l1 = strlen(s1);
        l2 = strlen(s2);
        printf("%d\n", DP());
    }
    //system("pause");
    return ;
}

二刷