数据结构-二叉树的遍历实现笔记C++

二叉树的遍历实现，可以用递归的方法也可以用非递归的方法。非递归的方法可以借助栈（前序遍历，中序遍历，后序遍历），也可以借助队列（层次遍历）。本次笔记只使用了递归的方法来进行前序遍历，中序遍历，后序遍历，借助队列进行层次遍历。想要更细致的看一下二叉树的遍历推荐http://c.biancheng.net/data_structure/tree/。

要遍历的二叉树如下：

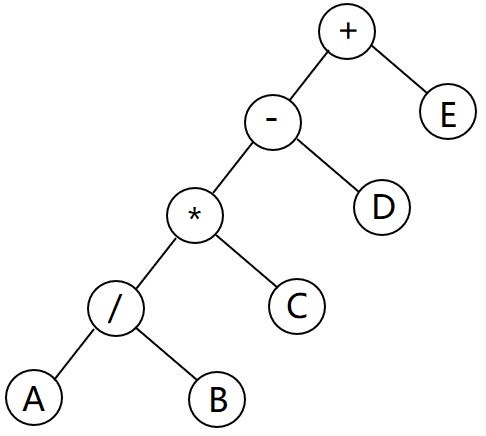
中序遍历：A/B*C-D+E
前序遍历：+-*/ABCDE
后序遍历：AB/C*D-E+
层次遍历：+-E*D/CAB

头文件代码

 #ifndef _BINARYTREE_H
 #define _BINARYTREE_H

 #include<iostream>
 #include<queue>

 template<class T> class BinaryTree;

 template<class T>
 class TreeNode
 {
 public:
     TreeNode()
     {
         leftChild = NULL;
         rightChild = NULL;
     }
     T data;
     TreeNode<T> *leftChild;
     TreeNode<T> *rightChild;
 };

 template<class T>
 class BinaryTree
 {
 public:
     //二叉树可以进行的操作
     void InOrder();//中序遍历
     void InOrder(TreeNode<T>* currentNode);

     void PreOrder();//前序遍历
     void PreOrder(TreeNode<T>* currentNode);

     void PostOrder();//后续遍历
     void PostOrder(TreeNode<T>* currentNode);

     void LevelOrder();//层次遍历
     void Visit(TreeNode<T>* currentNode);
 public:
     TreeNode<T> *root;//为方便使用将根节点设为公有
 };

 template<class T>
 void BinaryTree<T>::LevelOrder()
 {
     std::queue<TreeNode<T>*> q;//借用队列，先把每层元素放进队列再进行遍历
     TreeNode<T>* currentNode = root;
     while (currentNode)
     {
         Visit(currentNode);
         //由于队列先进先出，所以先放左子树，再放右子树
         if (currentNode->leftChild) q.push(currentNode->leftChild);
         if (currentNode->rightChild) q.push(currentNode->rightChild);
         if (q.empty()) return;
         currentNode = q.front();
         q.pop();//遍历之后要取走接着下一个
     }
 }

 template<class T>
 void BinaryTree<T>::Visit(TreeNode<T>* currentNode)
 {
     std::cout << currentNode->data;
 }

 template<class T>
 void BinaryTree<T>::InOrder()
 {
     InOrder(root);
 }

 template<class T>
 void BinaryTree<T>::InOrder(TreeNode<T>* currentNode)
 {
     if (currentNode)
     {
         InOrder(currentNode->leftChild);
         Visit(currentNode);
         InOrder(currentNode->rightChild);
     }
 }

 template<class T>
 void BinaryTree<T>::PreOrder()
 {
     PreOrder(root);
 }

 template<class T>
 void BinaryTree<T>::PreOrder(TreeNode<T>* currentNode)
 {
     if (currentNode)
     {
         Visit(currentNode);
         PreOrder(currentNode->leftChild);
         PreOrder(currentNode->rightChild);
     }
 }

 template<class T>
 void BinaryTree<T>::PostOrder()
 {
     PostOrder(root);
 }

 template<class T>
 void BinaryTree<T>::PostOrder(TreeNode<T>* currentNode)
 {
     if (currentNode)
     {
         PostOrder(currentNode->leftChild);
         PostOrder(currentNode->rightChild);
         Visit(currentNode);
     }
 }

 #endif

源文件代码

 #include<iostream>
 #include"binarytree.h"

 using namespace std;

 int main()
 {
     BinaryTree<char> tree;
     TreeNode<char> 加, 减, 乘, 除, a, b, c, d, e;
     加.data = '+';
     减.data = '-';
     乘.data = '*';
     除.data = '/';
     a.data = 'A';
     b.data = 'B';
     c.data = 'C';
     d.data = 'D';
     e.data = 'E';

     tree.root = &加;
     加.leftChild = &减;
     加.rightChild = &e;
     减.leftChild = &乘;
     减.rightChild = &d;
     乘.leftChild = &除;
     乘.rightChild = &c;
     除.leftChild = &a;
     除.rightChild = &b;

     cout << "中序遍历：" ;
     tree.InOrder();//中序遍历
     cout << endl;

     cout << "前序遍历：" ;
     tree.PreOrder();//前序遍历
     cout << endl;

     cout << "后序遍历：" ;
     tree.PostOrder();//后序遍历
     cout << endl;

     cout << "层次遍历：";
     tree.LevelOrder();//层次遍历
     cout << endl;
     return ;
 }