【bzoj3288】Mato矩阵

题目大意：给定一个n阶行列式，第i行第j列为GCD(i,j)，求这个行列式的值

高斯消元之后发现对角线上的东西是phi

于是线性筛出所有的欧拉函数即可

 #include<algorithm>
 #include<iostream>
 #include<cstdlib>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<queue>
 using namespace std;

 typedef long long LL;

 #define MOD 1000000007
 #define N 1000010

 int n;
 int cnt;
 LL ans=;

 LL phi[N];
 int prime[N];

 bool vis[N];

 void init()
 {
     phi[]=;
     for (int i=;i<=n;i++)
     {
         if (!vis[i])
             prime[++cnt]=i,phi[i]=i-;
         for (int j=;prime[j]*i<=n;j++)
         {
             vis[prime[j]*i]=true;
             if (i%prime[j]==)
             {
                 phi[prime[j]*i]=phi[i]*prime[j];
                 break;
             }
             phi[prime[j]*i]=phi[i]*(prime[j]-);
         }
     }
 }

 int main()
 {
     scanf("%d",&n);
     init();
     for (int i=;i<=n;i++)
         ans=ans*phi[i]%MOD;
     printf("%lld",ans);
     return ;
 }

一开始看题表示不会矩阵的行列式的值，于是搜了一下，发现求起来比较复杂。于是继续翻，发现一种可以这样搞

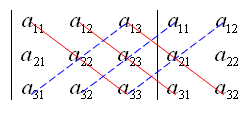
这里有一个ppt

http://wenku.baidu.com/link?url=fhxojDfArV5O6LtsJhOeS0l9za3jv58NRPciTQztWba_7X3bNw7dM3Kguxy8Qz2Okf_ohZ5rcf2QNNILrxQwtqKcAHZaQRglP6u1gYJYZ7C