codeforces 688C C. NP-Hard Problem(bfs判断奇数长度环)

题目链接：

C. NP-Hard Problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Recently, Pari and Arya did some research about NP-Hard problems and they found the minimum vertex cover problem very interesting.

Suppose the graph G is given. Subset A of its vertices is called a vertex cover of this graph, if for each edge uv there is at least one endpoint of it in this set, i.e. 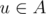 or  (or both).

Pari and Arya have won a great undirected graph as an award in a team contest. Now they have to split it in two parts, but both of them want their parts of the graph to be a vertex cover.

They have agreed to give you their graph and you need to find two disjoint subsets of its vertices A and B, such that both A and B are vertex cover or claim it's impossible. Each vertex should be given to no more than one of the friends (or you can even keep it for yourself).

Input

The first line of the input contains two integers n and m (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of vertices and the number of edges in the prize graph, respectively.

Each of the next m lines contains a pair of integers ui and vi (1  ≤  ui,  vi  ≤  n), denoting an undirected edge between ui and vi. It's guaranteed the graph won't contain any self-loops or multiple edges.

Output

If it's impossible to split the graph between Pari and Arya as they expect, print "-1" (without quotes).

If there are two disjoint sets of vertices, such that both sets are vertex cover, print their descriptions. Each description must contain two lines. The first line contains a single integer k denoting the number of vertices in that vertex cover, and the second line contains kintegers — the indices of vertices. Note that because of m ≥ 1, vertex cover cannot be empty.

Examples

input

4 2
1 2
2 3

output

1
2 
2
1 3 

input

3 3
1 2
2 3
1 3

output

-1

题意：

给一个森林,问能否找到这样的两个集合,使每条边的至少一个点在这样的集合里;有的话输出这两个集合;

思路：

每一条边的两个点分别是这两个集合里的;如果出现奇数长度的环就怎么也无法满足了;

AC代码：

//#include <bits/stdc++.h>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef  long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<''||CH>'';F= CH=='-',CH=getchar());
    for(num=;CH>=''&&CH<='';num=num*+CH-'',CH=getchar());
    F && (num=-num);
}
int stk[], tp;
template<class T> inline void print(T p) {
    if(!p) { puts(""); return; }
    while(p) stk[++ tp] = p%, p/=;
    while(tp) putchar(stk[tp--] + '');
    putchar('\n');
}

const LL mod=1e9+;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e5+;
const int maxn=;
const double eps=1e-;

int n,m;
vector<int>ve[N];
int dis[N],vis[N],ansa[N],ansb[N];
queue<int>qu;

int bfs(int x)
{
    vis[x]=;
    while(!qu.empty())qu.pop();
    qu.push(x);
    while(!qu.empty())
    {
        int fr=qu.front();
        qu.pop();
        int len=ve[fr].size();
        for(int i=;i<len;i++)
        {
            int y=ve[fr][i];
            if(!vis[y])
            {
                dis[y]=dis[fr]+;
                qu.push(y);
                vis[y]=;
            }
            else
            {
                if((dis[y]+dis[fr])%==)return ;
            }
        }
    }
    return ;
}
int check()
{
    for(int i=;i<=n;i++)
    {
        if(!vis[i])
        {
            dis[i]=;
           if( bfs(i)==)return ;
        }
    }
    return ;
}
int main()
{

        read(n);read(m);
        int u,v;
        for(int i=;i<m;i++)
        {
            read(u);read(v);
            ve[u].push_back(v);
            ve[v].push_back(u);
        }
        if(!check())cout<<"-1"<<"\n";
        else
        {
            int A=,B=;
            for(int i=;i<=n;i++)
            {
                if(dis[i]&)ansa[A++]=i;
                else ansb[B++]=i;
            }
            cout<<A<<"\n";
            for(int i=;i<A-;i++)printf("%d ",ansa[i]);
            printf("%d\n",ansa[A-]);
            cout<<B<<"\n";
            for(int i=;i<B-;i++)printf("%d ",ansb[i]);
            printf("%d\n",ansb[B-]);

        }

        return ;
}