【NJU749D】triple（莫比乌斯反演）

题意：

cas<=100 n<=10^5

思路：与两个数的没什么区别

F(d)=(n div d)*(n div d-1)*(n div d-2) div 6

再加上喜闻乐见的下底函数分块

又是一个不能测P的萎靡题库……

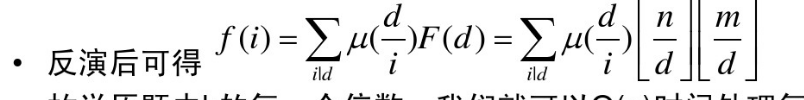
 const max=;
 var mu,flag,prime:array[..max]of longint;
     sum:array[..max]of int64;
     n,m,v,pos,i,j,t,cas:longint;
     ans,x:int64;
 begin
  assign(input,'triple.in'); reset(input);
  assign(output,'triple.out'); rewrite(output);
  mu[]:=;
  for i:= to max do
  begin
   if flag[i]= then
   begin
    inc(m); prime[m]:=i;
    mu[i]:=-;
   end;
   j:=;
   while (j<=m)and(prime[j]*i<=max) do
   begin
    t:=prime[j]*i; flag[t]:=;
    if i mod prime[j]= then
    begin
     mu[t]:=;
     break;
    end;
    mu[t]:=-mu[i];
    inc(j);
   end;
  end;
  for i:= to max do sum[i]:=sum[i-]+mu[i];
  readln(cas);
  for v:= to cas do
  begin
   readln(n,m);
   ans:=; i:=;
   n:=n div m;
   while i<=n do
   begin
    x:=n div i; pos:=n div x;
    ans:=ans+x*(x-)*(x-) div *(sum[pos]-sum[i-]);
    i:=pos+;
   end;
   writeln(ans);
  end;
  close(input);
  close(output);
 end.