C++实现顺序栈类求解中缀表达式的计算

控制台第一行打印的数值为使用形如以下方式得到的结果：

   cout << +*(+)*/- << endl;

即第一个待求解表达式由C++表达式计算所得结果，以用于与实现得出的结果作比较。

第1次测试：

第一个待求解表达式实现得出的结果比由C++表达式计算的结果大1，错误。

第2次测试：

第一个待求解表达式实现得出的结果与由C++表达式计算的结果完全一致；

第3与第5次测试：

实现无法求解取模运算；

第4次测试：

第一个待求解表达式实现得出的结果比由C++表达式计算的结果大1582，错误。

综上所述，实现用于计算一些表达式是正确可行的，而对于另外一些表达式则正确得出结果。另，由实现计算5/3*9与(5/3)*9的结果知：是否添加括号对实现能否正确计算表达式有直接关系。

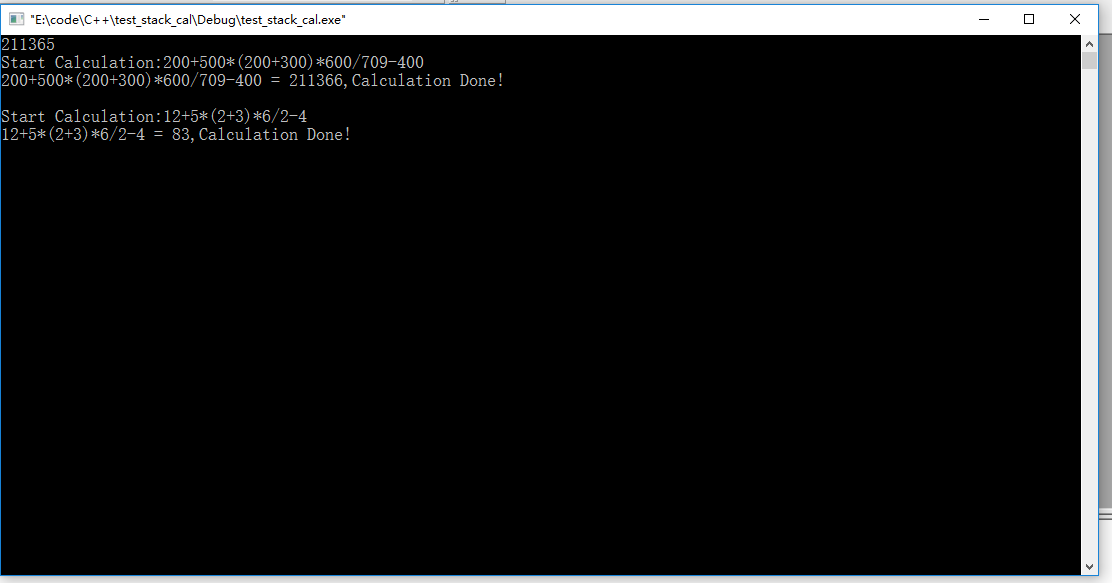
图1 求解200+500*(200+300)*600/709-400与5/3*9程序运行截图

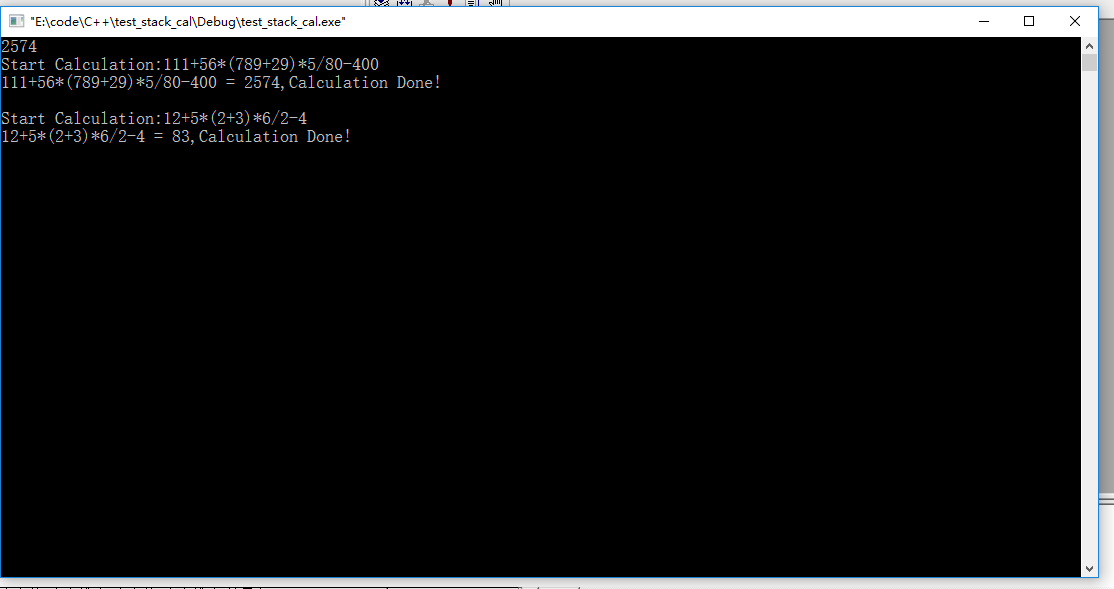
图2 求解111+56*(789+29)*5/80-400与12+5*(2+3)*6/2-4程序运行截图

图3 求解222+555*(777+111)*666/888-999/333+444+(34%7)与(5/3)*9程序运行截图

图4 求解222+555*(777+111)*666/888-999/333+444+(347)与(5/3)*9程序运行截图

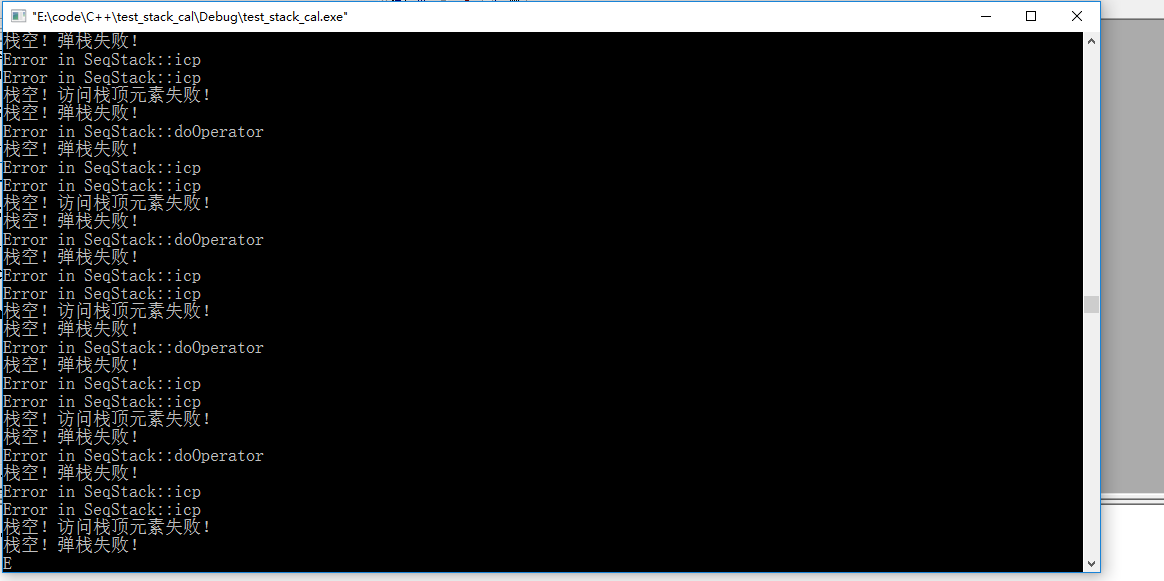
图5 计算222+555*(777+111)*666/888-999/333+444+(347)与9%3程序运行截图

下面上源代码：

存储元素类型为int的顺序栈类C++描述框架：

 //存储元素类型为int的顺序栈类C++描述框架：
 // SeqStack1.h: interface for the SeqStack class.
 //
 //////////////////////////////////////////////////////////////////////

 #if !defined(AFX_SEQSTACK1_H__55EE245C_A5F8_47D4_9510_B3BA6C85FF63__INCLUDED_)
 #define AFX_SEQSTACK1_H__55EE245C_A5F8_47D4_9510_B3BA6C85FF63__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 #include "charSeqStack.h"

 typedef double elementType;
 class SeqStack
 {
 public:
     SeqStack();
     virtual ~SeqStack();
     bool stackEmpty();
     bool stackFull();
     bool getTop( elementType& value );
     bool push( elementType value );
     bool pop();
     int length();
     void displayStack();
     int isp( elementType1 _operator );//栈内优先级
     int icp( elementType1 _operator );//栈外优先级
     charSeqStack css;
     double doOperator( elementType value1, elementType value2, elementType1 _operator );
     void calculate( char* Str );

     friend ostream &operator<< (ostream &os, const SeqStack &a)
     {
         for (int i = ; i < a.top + ; i++)
         {
             if (a.top == -)
                 return os;
             os << a.data[i];
         }

         return os;
     }

 private:
     elementType data[maxLength];
     int top;
 };

 #endif // !defined(AFX_SEQSTACK1_H__55EE245C_A5F8_47D4_9510_B3BA6C85FF63__INCLUDED_)

存储元素类型为char的顺序栈类C++描述框架：

 //存储元素类型为char的顺序栈类C++描述框架：
 // charSeqStack.h: interface for the charSeqStack class.
 //
 //////////////////////////////////////////////////////////////////////

 #if !defined(AFX_CHARSEQSTACK_H__A9958AD3_333A_41B4_B399_B6895C7AA8C5__INCLUDED_)
 #define AFX_CHARSEQSTACK_H__A9958AD3_333A_41B4_B399_B6895C7AA8C5__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 typedef char elementType1;
 const int maxLength =  + ;

 class charSeqStack
 {
 public:
     charSeqStack();
     virtual ~charSeqStack();
     bool stackEmpty();
     bool stackFull();
     bool getTop( elementType1& value );
     bool push( elementType1 value );
     bool pop();
     int length();
     int topValue();
     void displayStack();
     friend ostream &operator<< (ostream &os, const charSeqStack &a)
     {
         for (int i = ; i < a.top + ; i++)
         {
             if (a.top == -)
                 return os;
             os << a.data[i];
         }

         return os;
     }

 private:
     elementType1 data[maxLength];
     int top;
 };

 #endif // !defined(AFX_CHARSEQSTACK_H__A9958AD3_333A_41B4_B399_B6895C7AA8C5__INCLUDED_)

存储元素类型为int的顺序栈类C++实现：

 //存储元素类型为int的顺序栈类C++实现：
 // SeqStack1.cpp: implementation of the SeqStack class.
 //
 //////////////////////////////////////////////////////////////////////

 #include "stdafx.h"
 #include "SeqStack.h"

 //////////////////////////////////////////////////////////////////////
 // Construction/Destruction
 //////////////////////////////////////////////////////////////////////

 SeqStack::SeqStack()
 {
     top = -;
 }

 SeqStack::~SeqStack()
 {
 }

 bool SeqStack::stackEmpty()
 {
     return top == -;
 }

 bool SeqStack::stackFull()
 {
     return top == maxLength - ;
 }

 bool SeqStack::getTop( elementType& value )
 {
     if( stackEmpty() )
     {
         cout << "栈空！访问栈顶元素失败！" << endl;
         return false;
     }
     value = data[top];
     return true;
 }

 bool SeqStack::push( elementType value )
 {
     if( stackFull() )
     {
         cout << "栈满！压栈失败！" << endl;
         return false;
     }
     top ++;
     data[top] = value;
     return true;
 }

 bool SeqStack::pop()
 {
     if( stackEmpty() )
     {
         cout << "栈空！弹栈失败！" << endl;
         return false;
     }
     top --;
     return true;
 }

 int SeqStack::length()
 {
     if( stackEmpty() )
     {
         cout << "栈空！" << endl;
         return -;
     }
     return top + ;
 }

 void SeqStack::displayStack()
 {
     if( stackEmpty() )
     {
         cout << "栈空！无法打印！" << endl;
         return;
     }
     int column = ;
     for( int i = ; i <= top; i ++ )
     {
         cout << setw() << setiosflags( ios::left ) << data[i];
         column ++;
         if( column %  ==  )
             cout << endl;
     }
 }

 int SeqStack::isp( char _operator )
 {
     switch(_operator)
     {
     case '#' :
         return ;
         break;
     case '(':
         return ;
         break;
     case '*':
         return ;
         break;
     case '/':
         return ;
         break;
     case '+':
         return ;
         break;
     case '-':
         return ;
         break;
     case ')':
         return ;
         break;
     }

     cerr << "Error in SeqStack::isp" << endl;
     return -;
 }

 int SeqStack::icp( char _operator )
 {
     switch(_operator)
     {
     case '#' :
         return ;
         break;
     case '(':
         return ;
         break;
     case '*':
         return ;
         break;
     case '/':
         return ;
         break;
     case '+':
         return ;
         break;
     case '-':
         return ;
         break;
     case ')':
         return ;
         break;
     }

     cerr << "Error in SeqStack::icp" << endl;
     return -;
 }

 double SeqStack::doOperator( elementType value1, elementType value2, elementType1 _operator )
 {
     switch(_operator)
     {
     case '+':
         return value1 + value2;
         break;
     case '-':
         return value1 - value2;
         break;
     case '*':
         return value1 * value2;
         break;
     case '/':
         if( fabs(value2) < 0.0001 )
         {
             cout << "Divided by 0!" << endl;
             return -;
         }
         else
             return value1 / value2;
         break;
     }

     cerr << "Error in SeqStack::doOperator" << endl;
     return -;
 }

 void SeqStack::calculate( char* Str )
 {
     charSeqStack css1;
     char ch1;
     int i = ;
     double a, b;

     int level = ;
     int temp = ;

     while ( Str[i] != '\0' )
     {
         i ++;
     }
     i = i - ;
     while( css1.topValue() != - || Str[i] != '#' )
     {
         char ch = Str[i];
         if ( isdigit(ch) )
         {
             temp = temp + pow( , level ) * int( ch - '' );
             level ++;
             i --;
         }
         else
         {
             if (level)
             {
                 push(temp);
                 temp = ;
                 level = ;
             }
             css1.getTop(ch1);
             if ( ch1 == ')' && ch == '(' )
             {
                 css1.pop();
                 i --;
                 continue;
             }
             if ( isp(ch1) < icp(ch) )
             {
                 css1.push(ch);
                 i --;
             }
             else if (isp(ch1) >= icp(ch))
             {
                 getTop(a);
                 pop();
                 getTop(b);
                 pop();
                 push( doOperator( a, b, ch1 ) );
                 css1.pop();
             }
         }
     }

     if (level)
     {
         push(temp);
     }

 }

存储元素类型为char的顺序栈类C++实现：

 //存储元素类型为char的顺序栈类C++实现：

 // charSeqStack.cpp: implementation of the charSeqStack class.
 //
 //////////////////////////////////////////////////////////////////////

 #include "stdafx.h"
 #include "charSeqStack.h"

 using namespace std;
 //////////////////////////////////////////////////////////////////////
 // Construction/Destruction
 //////////////////////////////////////////////////////////////////////

 charSeqStack::charSeqStack()
 {
     top = -;
 }

 charSeqStack::~charSeqStack()
 {

 }

 bool charSeqStack::stackEmpty()
 {
     return top == -;
 }

 bool charSeqStack::stackFull()
 {
     return top == maxLength - ;
 }

 bool charSeqStack::getTop( elementType1& value )
 {
     ios::sync_with_stdio(false);
     if( stackEmpty() )
     {
         value = '#';
         //cout << "栈空！访问栈顶元素失败！charSeqStack" << endl;
         return false;
     }
     value = data[top];
     return true;
 }

 bool charSeqStack::push( elementType1 value )
 {
     ios::sync_with_stdio(false);
     if( stackFull() )
     {
         cout << "栈满！压栈失败！" << endl;
         return false;
     }
     top ++;
     data[top] = value;
     return true;
 }

 bool charSeqStack::pop()
 {
     if( stackEmpty() )
     {
         cout << "栈空！弹栈失败！" << endl;
         return false;
     }
     top --;
     return true;
 }

 int charSeqStack::length()
 {
     if( stackEmpty() )
     {
         cout << "栈空！" << endl;
         return -;
     }
     return top + ;
 }

 void charSeqStack::displayStack()
 {
     if( stackEmpty() )
     {
         cout << "栈空！无法打印！" << endl;
         return;
     }
     int column = ;
     for( int i = ; i <= top; i ++ )
     {
         cout << setw() << setiosflags( ios::left ) << data[i];
         column ++;
         if( column %  ==  )
             cout << endl;
     }
 }

 int charSeqStack::topValue()
 {
     return top;
 }