CodeForces 438D 线段树 剪枝

D. The Child and Sequence

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.

Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:

1. Print operation l, r. Picks should write down the value of .
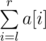2. Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
3. Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).

Can you help Picks to perform the whole sequence of operations?

Input

The first line of input contains two integer: n, m (1 ≤ n, m ≤ 10⁵). The second line contains n integers, separated by space: a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 10⁹) — initial value of array elements.

Each of the next m lines begins with a number type .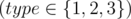

• If type = 1, there will be two integers more in the line: l, r (1 ≤ l ≤ r ≤ n), which correspond the operation 1.
• If type = 2, there will be three integers more in the line: l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 10⁹), which correspond the operation 2.
• If type = 3, there will be two integers more in the line: k, x (1 ≤ k ≤ n; 1 ≤ x ≤ 10⁹), which correspond the operation 3.

Output

For each operation 1, please print a line containing the answer. Notice that the answer may exceed the 32-bit integer.

Sample test(s)

Input

5 5 1 2 3 4 5 2 3 5 4 3 3 5 1 2 5 2 1 3 3 1 1 3

Output

8 5

Input

10 10 6 9 6 7 6 1 10 10 9 5 1 3 9 2 7 10 9 2 5 10 8 1 4 7 3 3 7 2 7 9 9 1 2 4 1 6 6 1 5 9 3 1 10

Output

49 15 23 1 9

Note

Consider the first testcase:

• At first, a = {1, 2, 3, 4, 5}.
• After operation 1, a = {1, 2, 3, 0, 1}.
• After operation 2, a = {1, 2, 5, 0, 1}.
• At operation 3, 2 + 5 + 0 + 1 = 8.
• After operation 4, a = {1, 2, 2, 0, 1}.
• At operation 5, 1 + 2 + 2 = 5.

注意：剪枝：若x<mod,x=x;

 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<map>

 #define N 100010
 #define M 15
 //#define mod 1000000007
 //#define mod2 100000000
 #define ll long long
 #define maxi(a,b) (a)>(b)? (a) : (b)
 #define mini(a,b) (a)<(b)? (a) : (b)

 using namespace std;

 int n,q;
 int x[N];
 int type;
 int a,b,c;

 struct node
 {
     ll sum;
     int ma;
 }tree[*N];
 /*
 void update(int l,int r,int i)
 {
     if(!tree[i].mark) return;
     int mid=(l+r)/2;
     tree[2*i].sum+=tree[i].mark*(ll)(mid-l+1);
     tree[2*i+1].sum+=tree[i].mark*(ll)(r-mid);
     tree[2*i].mark+=tree[i].mark;
     tree[2*i+1].mark+=tree[i].mark;
     tree[i].mark=0;

 }*/

 ll query(int tl,int tr,int l,int r,int i)
 {
     if(tl>r || tr<l)
         return ;
     if(tl<=l && r<=tr)
         return tree[i].sum;
    // update(l,r,i);
     int mid=(l+r)/;

     return query(tl,tr,l,mid,*i)+query(tl,tr,mid+,r,*i+);
 }
 /*
 void addd(int tl,int tr,int l,int r,int i,int val)
 {
     if(tl>r || tr<l)
         return;
     if(tl<=l && tr>=r){
         tree[i].sum+=val*(ll)(r-l+1);
         tree[i].mark+=val;
         return;
     }
     update(l,r,i);
     int mid=(l+r)/2;
     addd(tl,tr,l,mid,2*i,val);
     addd(tl,tr,mid+1,r,2*i+1,val);
     tree[i].sum=tree[2*i].sum+tree[2*i+1].sum;
 }*/

 void modefiyMod(int tl,int tr, int l, int r,int i,int mod)
 {
     if(tree[i].ma<mod) return;
     if(l==r){
         tree[i].sum=tree[i].ma=tree[i].sum%mod;
         return;
     }
     else{
         int mid=(l+r)/;
         if(tr<=mid){
             modefiyMod(tl,tr,l,mid,i*,mod);
         }
         else if(tl>mid){
             modefiyMod(tl,tr,mid+,r,i*+,mod);
         }
         else{
             modefiyMod(tl,tr,l,mid,i*,mod);
             modefiyMod(tl,tr,mid+,r,i*+,mod);
         }
         tree[i].sum=tree[*i].sum+tree[*i+].sum;
         tree[i].ma=max(tree[*i].ma,tree[*i+].ma);
     }
 }

 void setVal(int i, int l, int r,int x,int v)
 {
     if(l==r){
         tree[i].sum=tree[i].ma=v;
         return;
     }
     else{
         int mid=(l+r)/;
         if(x<=mid){
             setVal(i*,l,mid,x,v);
         }
         else{
             setVal(i*+,mid+,r,x,v);
         }
         tree[i].sum=tree[*i].sum+tree[*i+].sum;
         tree[i].ma=max(tree[*i].ma,tree[*i+].ma);
     }
 }

 void build_tree(int l,int r,int i)
 {
     if(l==r){
         tree[i].sum=x[l];
         tree[i].ma=x[l];
         return;
     }
     int mid=(l+r)/;
     build_tree(l,mid,*i);
     build_tree(mid+,r,*i+);
     tree[i].sum=tree[*i].sum+tree[*i+].sum;
     tree[i].ma=max(tree[*i].ma,tree[*i+].ma);
 }

 int main()
 {
     int i;
     //freopen("data.in","r",stdin);
     //scanf("%d",&T);
     //for(int cnt=1;cnt<=T;cnt++)
     //while(T--)
     while(scanf("%d%d",&n,&q)!=EOF)
     {
        for(i=;i<=n;i++) scanf("%d",&x[i]);
        memset(tree,,sizeof(tree));
        build_tree(,n,);
        while(q--){
             scanf("%d",&type);
             if(type==){
                 scanf("%d%d",&a,&b);
                 ll ans=query(a,b,,n,);
                 printf("%I64d\n",ans);

             }
             else if(type==){
                 scanf("%d%d%d",&a,&b,&c);
                 modefiyMod(a, b, , n, , c);
             }
             else{
                 scanf("%d%d",&a,&b);
                 setVal(, , n, a, b);
             }
        }
     }

     return ;
 }