【思维题 费用流 技巧】bzoj5403: marshland

主要还是网络流拆点建图一类技巧吧

Description

JudgeOnline/upload/201806/1(4).pdf

---

题目分析

第一眼看到这题时候只会把每个点拆成4个方向；再强制定向连边防止成环；最后做一遍最大费用可行流。

然而这种做法显然比较复杂，且关于强制定向我也并不是很熟练……

再仔细研究一下题目的性质，发现危险度所处的格子奇偶性是相同的。这种性质使得我们可以以黑白染色的角度考虑强制定向的问题。

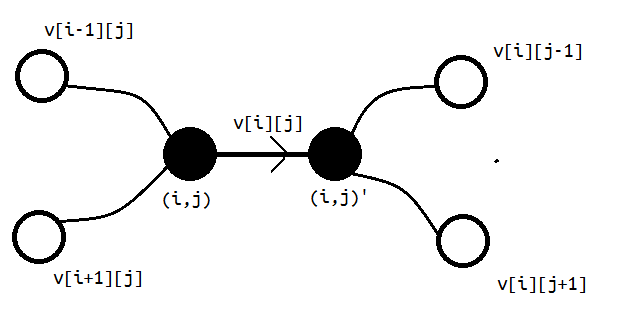
设$X+Y$为奇数的点为黑点；为偶数的点为白点。那么“折形”的限制就表述为每当选了一个黑点，就在上下、左右各选一个白点相连。对于费用流的建模，我们可以看做黑点放在中间，上下的白点在左边连向黑点；左右的白点在右边与黑点相连。首先来看中间的黑点，为了从费用流角度表示选取黑点，当然就是拆点连费用为$v[i][j]$的边。再是黑点两侧的点，需要注意的有：一、此处只是表示出了全图的一个部分，这里的白点还会和其他黑点产生关系，因此“两侧”的白点区别应当从所属行的奇偶性考虑。二、既然已经对黑点强制定向，那么“两侧”的白点就当分类分别处理与$S,T$的连边。

从这个角度建模后，由于对于每一个黑点都有关于相邻白点的$S,T$通路，那么每增广一次必然是在最大流的前提下保证选了当前最大费用。之所以提这一点，是因为有一些不恰当的建图方式把以S为起点的拓扑序安排得很混乱，以至于各个危险点之间的选取并不是完全分离的过程。

那么，剩下的就是一遍最大费用可行流的事情了。

 #include<bits/stdc++.h>
 typedef long long ll;
 const int maxn = ;
 const int maxNode = ;
 const int maxm = ;
 const int INF = 2e9;

 struct Edge
 {
     int u,v,f,c,cst;
     Edge(int a=, int b=, int c=, int d=, int e=):u(a),v(b),f(c),c(d),cst(e) {}
 }edges[maxm];
 int n,lim,k,S,T;
 int id[maxn][maxn],v[maxn][maxn];
 int edgeTot,head[maxNode],nxt[maxm],bck[maxNode],flw[maxNode];
 ll ans,cst[maxNode];
 bool inq[maxNode],chk;

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void addedge(int u, int v, int c, int cst)
 {
     edges[edgeTot] = Edge(u, v, , c,  cst), nxt[edgeTot] = head[u], head[u] = edgeTot, ++edgeTot;
     edges[edgeTot] = Edge(v, u, , , -cst), nxt[edgeTot] = head[v], head[v] = edgeTot, ++edgeTot;
 }
 void maxFlow()
 {
     std::queue<int> q;
     memset(bck, , sizeof bck);
     memset(flw, , sizeof flw);
     memset(cst, -0x3f3f3f3f, sizeof cst);
     q.push(S), flw[S] = INF, cst[S] = ;
     for (int tmp; q.size(); )
     {
         tmp = q.front(), q.pop(), inq[tmp] = ;
         for (int i=head[tmp]; i!=-; i=nxt[i])
         {
             int v = edges[i].v;
             if (cst[tmp]+edges[i].cst > cst[v]&&edges[i].f < edges[i].c){
                 cst[v] = cst[tmp]+edges[i].cst, bck[v] = i;
                 flw[v] = std::min(flw[tmp], edges[i].c-edges[i].f);
                 if (!inq[v]) inq[v] = , q.push(v);
             }
         }
     }
     if (cst[T] < ) chk = false;
     else{
         for (int i=T; i!=S; i=edges[bck[i]].u)
             edges[bck[i]].f += flw[T], edges[bck[i]^].f -= flw[T];
         ans -= cst[T]*flw[T];
     }
 }
 int main()
 {
     memset(head, -, sizeof head);
     n = read(), lim = read(), k = read();
     S = , T = n*n*+;
     for (int i=, cnt=; i<=n; i++)
         for (int j=; j<=n; j++)
             id[i][j] = ++cnt, v[i][j] = read(), ans += v[i][j];
     for (; k; --k) v[read()][read()] = INF;
     for (int i=; i<=n; i++)
         for (int j=; j<=n; j++)
             if (v[i][j]!=INF){
                 if ((i+j)&) addedge(id[i][j], id[i][j]+n*n, , v[i][j]);
                 else{
                     if (i&){
                         addedge(S, id[i][j], , );
                         if (i > ) addedge(id[i][j], id[i-][j], , );
                         if (i < n) addedge(id[i][j], id[i+][j], , );
                         if (j > ) addedge(id[i][j], id[i][j-], , );
                         if (j < n) addedge(id[i][j], id[i][j+], , );
                     }else{
                         addedge(id[i][j], T, , );
                         if (i > ) addedge(id[i-][j]+n*n, id[i][j], , );
                         if (i < n) addedge(id[i+][j]+n*n, id[i][j], , );
                         if (j > ) addedge(id[i][j-]+n*n, id[i][j], , );
                         if (j < n) addedge(id[i][j+]+n*n, id[i][j], , );
                     }
                 }
             }
     chk = true;
     for (; lim&&chk; --lim) maxFlow();
     printf("%lld\n",ans);
     return ;
 }

END