机器学习之逻辑回归（logistic回归）

前言

           以下内容是个人学习之后的感悟，转载请注明出处~

逻辑回归

一、为什么使用logistic回归

　   一般来说，回归不用在分类问题上，因为回归是连续型模型，而且受噪声影响比较大。

Why?  为什么回归一般不用在分类上？其实，很多初学者都会提出这个问题。然而，文字的解释往往不能说服我们，接下来

用图示的方式为大家讲解。

以最简单的分类为例，当y≥0.5时，输出“1”；当y<0.5时，输出“0”。下面左图，数据样本较好，线性回归模型在y=0.5处的橘色分界线

刚好在“0”、“1”两类样本的分界线处，完美地完成分类。然而，现实情况往往没有这么乐观，下面有图中出现了一个额外的样本，所谓的噪

声点，会使训练完毕的线性回归模型准确度变差。从右图中可以做直观地看到，线性回归模型在y=0.5处的粉色分界线将一个“1”类样本分类到

了“0”类样本集中，此时就出现了判断失误。

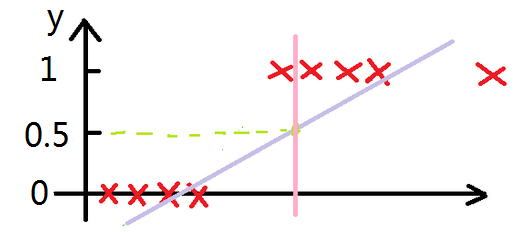
所以线性回归一般不用在分类问题上，如果非要用于分类，可以使用logistic回归。

逻辑回归为什么可以用在分类上？why?

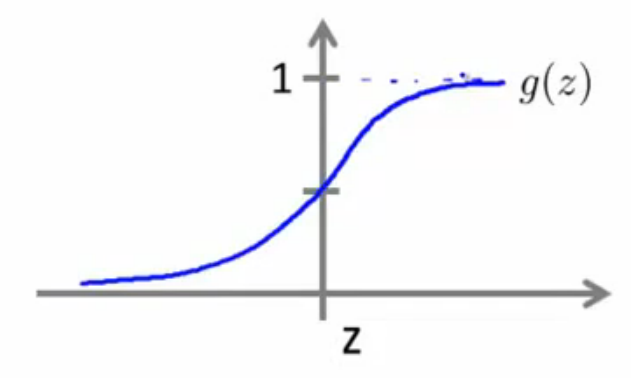
原因很简单，逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和θ^Tx，设为z，然后使用函

数g(z)作为假设函数来预测。g(z)可以将连续值映射到0和1上。如下图所示，当z≥0时，输出为1；当z<0时，输出为0。这样可以实现很好的分类。

具体实现请看下文~

二、logistic回归

• 假设函数：

• 初始代价函数：

（细心的童鞋会发现，这里的代价函数与线性回归模型中的J(θ₀，θ₁)不一样，其实就是整体误差和平均误差的区别。）

显然，由于S型函数的存在，代价函数是非凸函数，无法使用梯度下降法来求极小值。这就需要转换为下面的简易代价函数。

• 简易代价函数：

说实话，这一步，我也不知道是怎么推导的，有哪位大神知道的话，请不吝赐教~

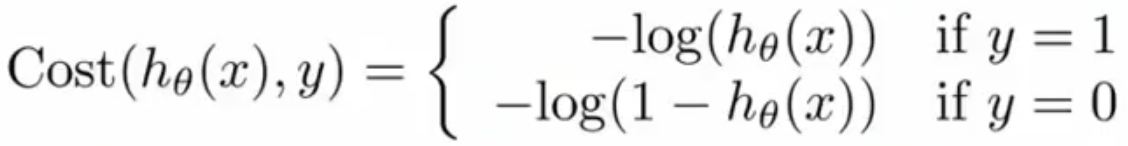
　　　　　　　　　  然而，要想使用梯度下降法，还需要转换为J(θ)代价函数

• J(θ)代价函数（凸函数）：

• 使用方法：

1、采用梯度下降法，不断迭代下列公式，直到收敛，求出θ。

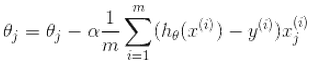
其推导过程如下：

细心的童鞋可能会注意到，逻辑回归和线性回归在梯度下降法中使用的迭代公式竟然一样。其实不然，不同点在于

迭代公式中的h_θ(x)：

逻辑回归：   

线性回归：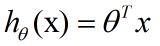    

2、判断θ^Tx的大小来分类。

“y=1”，当θ^Tx≥0

“y=0”，当θ^Tx<0

（很容易发现θ^Tx=0是分类的决策边界）

三、多分类逻辑回归

使用逻辑回归算法进行多分类时，可以设其中一类为1，其他都为0，建立一个分类器，以此类推，遍历全部类别，建立N个分类器。

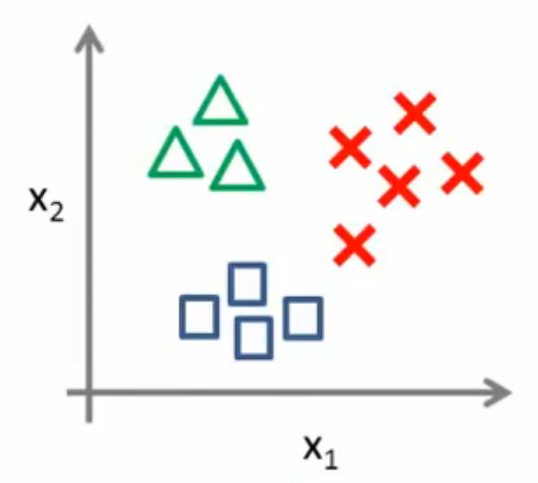
如下表所示，总共3个类别，因此设立3个分类器，每个分类器的样本训练由上文中的二分类步骤完成。

		三角形设为1，其他设为0。作为分类器1，即hθ(1)(x)
		正方形设为1，其他设为0。作为分类器2，即hθ(2)(x)
		红十字设为1，其他设为0。作为分类器3，即hθ(3)(x)

每个分类器训练完毕后，取一个新的x数据，代入3个分类器中，哪个求出的h值最大，则这个分类器可信度最高，此分类器的“1”类别

就是此x的类别。

以上是全部内容，如果有什么地方不对，请在下面留言，谢谢~