关于可图化序列的一点结论 NEU 1429

Graphic Sequence

A graphic sequence is a sequence of numbers which can be the degree sequence of some graph. A sequence can be checked to determine if it is graphic using GraphicQ[g] in the Mathematica package Combinatorica` .

Erdős and Gallai (1960) proved that a degree sequence 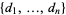 is graphic iff the sum of vertex degrees is even and the sequence obeys the property

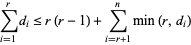for each integer 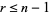 (Skiena 1990, p. 157), and this condition also generalizes to directed graphs. Tripathi and Vijay (2003) showed that this inequality need be checked only for as many  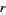as there are distinct terms in the sequence, not for all .

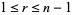Havel (1955) and Hakimi (1962) proved another characterization of graphic sequences, namely that a degree sequence with 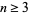=3" style="border-width: 0px; vertical-align: middle;"> and 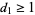=1" style="border-width: 0px; vertical-align: middle;"> is graphical iff the sequence  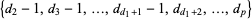is graphical. In addition, Havel (1955) and Hakimi (1962) showed that if adegree sequence is graphic, then there exists a graph  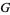such that the node of highest degree is adjacent to the  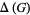next highest degree vertices of 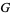, where  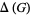is the maximum degree of .

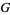No degree sequence can be graphic if all the degrees occur with multiplicity 1 (Behzad and Chartrand 1967, p. 158; Skiena 1990, p. 158). Any degree sequence whose sum is even can be realized by a multigraph having loops (Hakimi 1962; Skiena 1990, p. 158).

很不错的一个定理: 就是给出一个度序列，然后 判读这个度序列是不是可图的当且仅当 满足 ： sigma<1,r>(di) <= k*(k-1) +sigma<k+1,n> min(k,di)

(    0< k<=n   )

注意到定理中要求 sigma<k+1,n> min(k,di) ； 所以我们可以二分找出度数大于k的区间求出其前缀和即可 时间复杂的达到 O(nlogn) 然后套公式就行了。

其实还有另外一个定理： havel定理,不是怎么实用的定理感觉是 。 网上题解代码 复杂度都是O(n^2logn) 没事水数据玩都是。  还扯些没用的优化，

好像可以计数排序写复杂度是O(n^2) 省赛还是被卡掉的。 O(nlogn) 还挺快>_<。

给出一道题：

1429: Traveling

题目描述

SH likes traveling around the world. When he arrives at a city, he will ask the staff about the number of cities that connected with this city directly. After traveling around a mainland, SH will collate data and judge whether the data is correct.

A group of data is correct when it can constitute an undirected graph.

输入

There are multiple test cases. The first line of each test case is a positive integer N (1<=N<=10000) standing for the number of cities in a mainland. The second line has N positive integers a1, a2, ...,an. ai stands for the number of cities that connected directly with the ith city. Input will be ended by the END OF FILE.

输出

If a group of data is correct, output "YES" in one line, otherwise, output "NO".

样例输入

8 7 7 4 3 3 3 2 1 10 5 4 3 3 2 2 2 1 1 1 

样例输出

NO YES

1 #include<cstdio>

 2 #include<cstring>
 3 #include<algorithm>
 4 using namespace std;
 5 const int MAX = 1e5;
 6 int deg[MAX],sum[MAX],sum2[MAX];
 7 int cmp(int a,int b) {return a>b ;}
 8 int n;
 9 int check() {
     if(sum[n]&) return ;
     for(int k=;k<=n;k++) {
        int L=k+,R=n; int ans;
        while(L<=R) {
             int mid=(R+L) >> ;
             if(deg[mid]>=k) ans=mid,L=mid+;
             else R=mid-;
        }
        sum2[k]=k*(ans-k)+sum[n]-sum[ans];
     }
     int ans;
     for(int i=;i<=n;i++) {
         if(sum[i]<=i*(i-)) continue;
         ans=sum2[i];
        // for(int k=i+1;k<=n;k++) ans+=min(i,deg[k]);
         if(sum[i]>i*(i-)+ans) return ;
  
     }
     return ;
 }
  
 int main() {
     while(scanf("%d",&n)==) {
         memset(sum,,sizeof(sum));
         memset(sum2,,sizeof(sum2));
         for(int i=;i<=n;i++) scanf("%d",&deg[i]);
         sort(deg+,deg+n+,cmp);
         for(int i=;i<=n;i++) sum[i]=sum[i-] + deg[i];
         int ret=check();
         if(ret) printf("YES\n");
         else printf("NO\n");
     }
 }
  
 /**************************************************************
     Problem: 1429
     User: 20124906
     Language: C++
     Result: 正确
     Time:201 ms
     Memory:1960 kb
 ****************************************************************/