HDU 3594 Cactus 有向仙人掌图判定

题意

给出一个有向图，并给出仙人掌图的定义

1. 图本身是强连通的
2. 每条边属于且只属于一个环

判断输入的图是否是强连通的。

分析

杭电OJ上的数据比较弱，网上一些有明显错误的代码也能AC。

本着求真务实的精神，取网上查阅了相关资料，整理出来一个对自己来说还比较明确的算法。

从DFS森林说起

从有向图的某一点开始进行深度优先遍历，按照遍历的先后顺序会形成一棵树，像这种边被称作树边(Tree Edge)

当然有向图中还可能会存在一些其他的边：

• 从当前节点连向其祖先节点的边叫做反向边(Back Edge)
• 从当前节点连向其后代节点的边叫做前向边(Forward Edge)
• 从当前节点连向其他节点，可能是某个祖先其他分支的节点或者另一颗DFS树的节点，这种边叫做交叉边(Cross Edge)
  
  

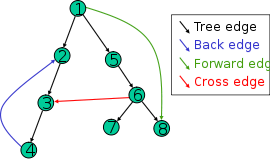
按边的分类考虑仙人掌图

接下来默认图是强连通的，后面不再强调。

1. 如果\(u \to v\)是一条前向边，必然有一条从\(v\)到\(u\)的路径\(Path\)。这样\(Path\)就和前向边\(u \to v\)构成了一个环，同时也和树边上的\(u\)到\(v\)的路径构成了一个环，而且这两个环有公共路径\(Path\)。因此得到结论：仙人掌图中不含前向边。
2. 如果\(u \to v\)是一条交叉边，它们的最近公共祖先为\(anc\)。同样也有一条从\(v\)到\(anc\)的路径\(Path_{v \to anc}\)，这条路径和\(v\)到\(anc\)的路径或相交或不相交。同样也构成了两个有公共边的环，因此得到结论：仙人掌图中不含交叉边。
   
   

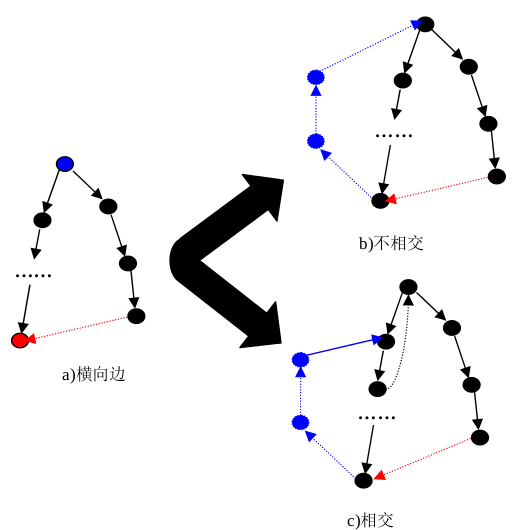
因此，除了树边只剩下反向边，而且可以看出每有一条反向边\(u \to v\)，它和树边上的路径\(v \to u\)构成了一个环。

下面想办法保证每条树边至多被一个环所包含：

• 一个点最多有一条反向边
• 在当前节点记录一个可以返回的最小的DFS序，保证反向边指向的节点的DFS序不能小于该值，否则会出现有公共边的两个环。

这是通过一遍DFS实现的。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <stack>
#include <vector>
using namespace std;

const int maxn = 10000 + 10;

int n, m;
vector<int> G[maxn];

stack<int> S;
int dfs_clock, pre[maxn], low[maxn];
int scc_cnt, sccno[maxn];

void dfs(int u) {
	pre[u] = low[u] = ++dfs_clock;
	S.push(u);
	for(int v : G[u]) {
		if(!pre[v]) {
			dfs(v);
			low[u] = min(low[u], low[v]);
		} else if(!sccno[v]) low[u] = min(low[u], pre[v]);
	}
	if(low[u] == pre[u]) {
		scc_cnt++;
		for(;;) {
			int x = S.top(); S.pop();
			sccno[x] = scc_cnt;
			if(x == u) break;
		}
	}
}

//Tarjan算法求强连通分量
void find_scc() {
	dfs_clock = scc_cnt = 0;
	memset(pre, 0, sizeof(pre));
	memset(sccno, 0, sizeof(sccno));
	for(int i = 0; i < n; i++) if(!pre[i])
		dfs(i);
}

//第二遍DFS保证是仙人掌图

//color[u]为0表示还没有访问，为1表示正在访问，为2表示已经访问完毕
int color[maxn];

bool dfs2(int u, int minBack) {    //minBack表示反向边能指向的最小的DFS序
	color[u] = 1;
	int backs = 0;//反向边的个数，至多只能有一个
	for(int v : G[u]) if(color[v] == 1) {    //找到一条反向边
		backs++;
		if(backs > 1) return false;
		if(pre[v] < minBack) return false;    //反向边指向的节点的DFS序小于最小值
	}
	if(backs) minBack = pre[u];
	for(int v : G[u]) {
		if(color[v] == 2) return false;    //前向边或交叉边
		if(color[v] == 0)    //树边
			if(!dfs2(v, minBack)) return false;;
	}
	color[u] = 2;
	return true;
}

int main()
{
	int T; scanf("%d", &T);
	while(T--) {
		scanf("%d%d", &n, &m);
		for(int i = 0; i < n; i++) G[i].clear();
		while(m--) {
			int u, v; scanf("%d%d", &u, &v);
			G[u].push_back(v);
		}

		find_scc();
		if(scc_cnt > 1) { puts("NO"); continue; }

		memset(color, 0, sizeof(color));
		if(!dfs2(0, 0)) puts("NO");
		else puts("YES");
	}

	return 0;

}

参考资料

1.仙人掌图分析

2.my solution注：这份代码没有考虑只能有一条反向边的限制，但也能在UVa上AC