UVa 1583 Digit Generator(数学)



题意 假设a加上a全部数位上的数等于b时 a称为b的generator  求给定数的最小generator

给的数n是小于100,000的  考虑到全部数位和最大的数99,999的数位和也才45  因此我们仅仅须要从n-45到n枚举即可了

#include<cstdio>
#include<cstring>
using namespace std;
int t, n, a, b, ans, l;
int main()
{
    scanf ("%d", &t);
    while (t--)
    {
        scanf ("%d", &n);
        ans = 0;
        for (int i = n-50; i < n; ++i)
        {
            a = b = i;
            while (b)
            {
                a += b % 10;
                b /= 10;
            }
            if (a + b == n)
            {
                ans = i;
                break;
            }
        }
        printf ("%d\n", ans);
    }
    return 0;
} 

For a positive integer N , the digit-sum of N is defined as the sum of N itself and its digits. When M is
the digitsum of N , we call N a generator of M .

For example, the digit-sum of 245 is 256 (= 245 + 2 + 4 + 5). Therefore, 245 is a generator of 256.

Not surprisingly, some numbers do not have any generators and some numbers have more than one generator. For example, the generators of 216 are 198 and 207.

You are to write a program to find the smallest generator of the given integer.

Input

Your program is to read from standard input. The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case takes one line
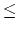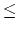containing an integer N , 1N100,
000 .

Output

Your program is to write to standard output. Print exactly one line for each test case. The line is to contain a generator of N for each test case. If N has multiple generators,
print the smallest. If N does not have any generators, print 0.

The following shows sample input and output for three test cases.

Sample
Input

3
216
121
2005

Sample
Output

198
0
1979