【CF 549G Happy Line】排序

题目链接：http://codeforces.com/problemset/problem/549/G

题意：给定一个n个元素的整数序列a[], 任意时刻对于任一对相邻元素a[i-1]、 a[i]，若a[i-1] < a[i] 则要依次执行如下两个操作：

　　1. a[i-1]--, a[i]++；

　　2. 交换a[i-1]和a[i]的位置。

经过若干次1、2操作后，若能使整个序列变成非降的，则输出最终的序列；否则输出":("。

数据范围：n 属于 [1, 2*10^5], a[i] 属于[0, 10^9]

思路：首先想到交换排序，但n 在10^5所以n^2的排序不可取。后来模拟快排的过程推出了样例，如下：

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <queue>
 #define CLEAR(A, X) memset(A, X, sizeof(A))
 #define REP(N) for(int i=0; i<(N); i++)
 #define REPE(N) for(int i=1; i<=(N); i++)
 #define FREAD(FN) freopen((FN), "r", stdin)
 #define pb(a) push_back(a)
 #define pf() pop_front()
 using namespace std;

 const int MAX_N = ;
 int n;
 int a[MAX_N];
 int flag;
 void partition(int s, int e){
     if(s == e) return ;
     int i = s, j = e - ;
     //printf("i %d j %d*******\n", i, j);
     while(i < j){
         while(i < j && a[j] >= a[i]) j--;
         if(i < j){
             a[j] += j - i;
             if(a[i] == a[j]){
                 flag = ;
                 return ;
             }
             a[i] -= j - i;
             swap(a[i], a[j]);
             i++;
         }

         while(i < j && a[i] <= a[j]) i++;
         if(i < j){
             a[i] -= j - i;
             if(a[i] == a[j]){
                 flag = ;
                 return ;
             }
             a[j] += j - i;
             swap(a[i], a[j]);
             j--;
         }
         // for(int k=0; k<n; k++) printf("%d ", a[k]);
         // printf("\n");
     }//i == j
     partition(s, i);
     partition(i+, e);
 }

 int main()
 {
     scanf("%d", &n);
     REP(n) scanf("%d", &a[i]);
     flag = ;
     partition(, n);
     if(flag) printf(":(\n");
     else{
         REP(n) printf("%d ", a[i]);
         printf("\n");
     }
     return ;
 }

quickSort，i, j相对往中间走

但对于第六个test（

5
15 5 8 6 3

）得到的结果是错的，尝试改用i, j 指针同方向走来构造轴点，如下，但还是构造不出正确的结果。

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <queue>
 #define CLEAR(A, X) memset(A, X, sizeof(A))
 #define REP(N) for(int i=0; i<(N); i++)
 #define REPE(N) for(int i=1; i<=(N); i++)
 #define FREAD(FN) freopen((FN), "r", stdin)
 #define pb(a) push_back(a)
 #define pf() pop_front()
 using namespace std;

 const int MAX_N = ;
 int n;
 int a[MAX_N];
 int flag;
 void partition(int s, int e){
     if(s == e) return ;
     int i = s, j = s + ;
     int cur = s;
     //printf("i %d j %d*******\n", i, j);
     while(i < e && j < e){
         while(i < j && j < e && a[j] >= a[i]) j++;
         if(i < j && j < e){
             a[j] += j - i;
             if(a[i] == a[j]){
                 flag = ;
                 return ;
             }
             a[i] -= j - i;
             swap(a[i], a[j]);
             cur = j;
             i = j + ;
         }

         while(j < i && i < e && a[i] >= a[j]) i++;
         if(j < i && i < e){
             a[j] -= i - j;
             if(a[i] == a[j]){
                 flag = ;
                 return ;
             }
             a[i] += i - j;
             swap(a[i], a[j]);
             cur = j;
             j = i + ;
         }
         // for(int k=0; k<n; k++) printf("%d ", a[k]);
         // printf("\n");
     }//i == j
     partition(s, cur);
     partition(cur+, e);
 }

 int main()
 {
     scanf("%d", &n);
     REP(n) scanf("%d", &a[i]);
     flag = ;
     partition(, n);
     if(flag) printf(":(\n");
     else{
         REP(n) printf("%d ", a[i]);
         printf("\n");
     }
     return ;
 }

quickSort，i, j从左往右走

于是看题解了，以下是题解的思路，思想仍是排序，（虽然tag上写了greedy，但我没想明白哪里用到了贪心策略）：

由于swap(a[i-1], a[i])时，向左的a[i]在数值上"收益"了1，向右的a[i-1]在数值上"消耗"了1，现在把由交换产生的“收益/消耗”变化量从a[i]的原始数值中分离开来。

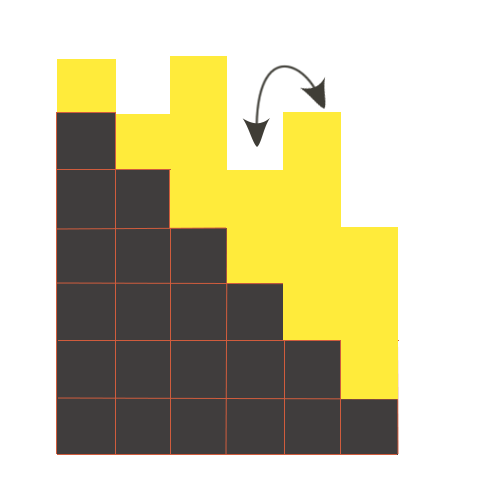
如左图，每一列对应一个位置 i ，其中黑色的“台阶”加上黄色的“塔”为原始的a[i]值，现在规定从左到右台阶的高度从n 均匀递减到 1, 记黄色的塔高 b[i] = 原始高度a[i] - 台阶高度(n - i)（i从0起始）；这样每个a[i] 向左交换相当于上一个台阶，向右交换为下一个台阶，对应的塔高b[i]是不变的，如右图。所以我们只需计算出序列b[i]并把它排成非降序，然后再加上对应位置的台阶高度就是最终结果了。对于":("的情况，只需得到结果后扫描一遍检查是否确实非降序即可。

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <queue>
 #define CLEAR(A, X) memset(A, X, sizeof(A))
 #define REP(N) for(int i=0; i<(N); i++)
 #define REPE(N) for(int i=1; i<=(N); i++)
 #define FREAD(FN) freopen((FN), "r", stdin)
 #define pb(a) push_back(a)
 #define pf() pop_front()
 using namespace std;

 const int MAX_N = ;
 int n;
 int a[MAX_N];
 int flag;

 int main()
 {
     scanf("%d", &n);
     REP(n) scanf("%d", &a[i]);
     flag = ;
     REP(n) a[i] -= n - i;
     sort(a, a+n);
     a[] += n;
     for(int i=; i<n; i++){
         a[i] += n - i;
         if(a[i] < a[i-]){
             flag = ;
             break;
         }
     }

     if(flag) printf(":(\n");
     else{
         REP(n) printf("%d ", a[i]);
         printf("\n");
     }
     return ;
 }