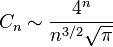卡特兰数 Catalan数 ( ACM 数论 组合 )

卡特兰数 Catalan数 ( ACM 数论 组合 )

Posted on 2010-08-07 21:51 MiYu 阅读(13170) 评论(1)  编辑 收藏 引用 所属分类: ACM ( 数论 ) 、ACM_资料 、ACM ( 组合 )

维基百科资料:

卡塔兰数

卡塔兰数是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。

卡塔兰数的一般项公式为                       另类递归式：  h(n)=((4*n-2)/(n+1))*h(n-1);

前几项为 （OEIS中的数列A000108）: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...

[编辑]性质

C_n的另一个表达形式为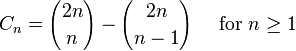 所以，C_n是一个自然数；这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。(见下文的第二个证明。)

卡塔兰数满足以下递推关系

它也满足

这提供了一个更快速的方法来计算卡塔兰数。

卡塔兰数的渐近增长为

它的含义是左式除以右式的商趋向于1当n → ∞。（这可以用n!的斯特灵公式来证明。）

所有的奇卡塔兰数C_n都满足n = 2^k − 1。所有其他的卡塔兰数都是偶数。

[编辑]应用

组合数学中有非常多.的组合结构可以用卡塔兰数来计数。在Richard P. Stanley的Enumerative Combinatorics: Volume 2一书的习题中包括了66个相异的可由卡塔兰数表达的组合结构。以下用C_n=3和C_n=4举若干例：

• C_n表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串，且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY

• 将上例的X换成左括号，Y换成右括号，C_n表示所有包含n组括号的合法运算式的个数:

((())) ()(()) ()()() (())() (()())

• C_n表示有n+1个叶子的二叉树的个数。

• C_n表示所有不同构的含n个分枝结点的满二叉树的个数。（一个有根二叉树是满的当且仅当每个结点都有两个子树或没有子树。）

证明：

令1表示进栈，0表示出栈，则可转化为求一个2n位、含n个1、n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有个，下面考虑不满足要求的数目.

考虑一个含n个1、n个0的2n位二进制数，扫描到第2m+1位上时有m+1个0和m个1（容易证明一定存在这样的情况），则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0，则对应一个n+1个0和n-1个1的二进制数。反之亦然（相似的思路证明两者一一对应）。

从而。证毕。

• C_n表示所有在n × n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数： X代表“向右”，Y代表“向上”。下图为n = 4的情况：
• 

• C_n表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数。下图中为n = 4的情况：

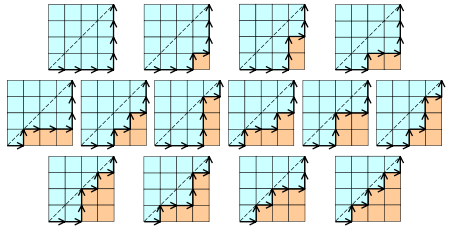
• C_n表示对{1, ..., n}依序进出栈的置换个数。一个置换w是依序进出栈的当S(w) = (1, ..., n), 其中S(w)递归定义如下：令w = unv，其中n为w的最大元素，u和v为更短的数列；再令S(w) =S(u)S(v)n，其中S为所有含一个元素的数列的单位元。

• C_n表示集合{1, ..., n}的不交叉划分的个数. 那么, C_n 永远不大于第n项贝尔数. C_n也表示集合{1, ..., 2n}的不交叉划分的个数，其中每个段落的长度为2。综合这两个结论，可以用数学归纳法证明 that all of the free cumulants of degree more than 2 of the Wigner semicircle law are zero. This law is important in free probability theory and the theory of random matrices.

• C_n表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为 n = 4的情况:

百度百科资料:
简介

　　中文:卡特兰数
　　Catalan数是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。
　　原理：
　　令h(0)=1,h(1)＝1,catalan数满足递归式：
　　h(n)= h(0)*h(n-1) + h(1)*h(n-2) +  + h(n-1)h(0) (其中n>=2)
　　该递推关系的解为：
　　h(n)=C(2n,n)/(n + 1) (n=1,2,3,)
       另类递归式：  h(n)=((4*n-2)/(n+1))*h(n-1);
　　
　　前几项为 （OEIS中的数列A000108）: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, 
应用

　　我总结了一下，最典型的四类应用：（实质上却都一样，无非是递归等式的应用，就看你能不能分解问题写出递归式了）
1.括号化问题。

　　矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)
2.出栈次序问题。

　　一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
　　类似：
　　(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
　　(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。
3.将多边行划分为三角形问题。

　　将一个凸多边形区域分成三角形区域的方法数?
　　类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她
　　从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
　　类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
4.给顶节点组成二叉树的问题。

　　给定N个节点，能构成多少种形状不同的二叉树？
　　(一定是二叉树!
　　先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +  + h(n-1)h(0)=h(n))
　　（能构成h（N）个）