n次单位根（n-th unit root）

最近在看CKKS方案，里面的编码/解码用到了n次单位根，感觉基于环上的加密，很多都会用到，现在系统的学习一下！

定义

先看定义：

\[z^n=1，(n=1,2,3,...)
\]

该方程的根z为n次单位根，就是说这些根是复数！

简单说：n次方根，就是多项式\(x^n-1\)或方程\(x^n-1=0\)在复数域内的n个不同的根，简称单位根

具体来讲，单位根有n次根的有n个：$$z_i=e^{2\pi ki/n },(k=0,1,2,..,n-1)$$

复数域内：$$x_k=cos(2k\pi/n)+sin(2k\pi/n)I,(k=0,1,2,..,n-1),i是虚数单位$$

举个例子：

其中提到了“本源根”，后面再去单独介绍！

性质

1、对于方程\(x^n-1=0\)，不同的我单位根只有n个

例如：取k=0,1,2,..,n-1，就得到n个不同的n次单位根

取\(k=q*n+m,(q\in \mathbb{Z}^+,m=(0,1,...,n-1))\)时，\(x_k=x_{q*n+m}=x_m\)

2、n次单位根的模为1，即\(|x_k|=1\)

3、两个n次单位根（\(x_i,x_j\)）的乘积，仍是一个n次单位根\(w_i*w_j=W_{i+j}\)，则：

（1）\((x_i)^{-1}=x_{-I}\)

（2）\((x_m)^{k}=x_{m*k}\)，（m，k是任意整数，当k=0时，\((x_m)^{0}=1=x_{0}\)）

（3）\(x_{m}=x_l\)：需要gcd(m,l)=1

（4）任何一个单位根都可以写为\(x_0\)的幂，如\(x_m=(x_1)^m\)，这种根叫做n次本原单位根，简称n次原根或原根。当p和n互素且\(1 \leqslant p < n\)时，\(x_1^p\)都是n次本原单位根

（5）一个n次单位根的共轭复数也是一个n次单位根，记 \(\overline{x}=x_{n-m}\)

（6）对于任意的l和r，都有\((x_i)^r=(x_r)^l\)

（7）若a是整数，则

\[1+x_1^a+x_2^a+...+x_{n-1}^a=\left\{\begin{matrix}
\\n,gcd(a,n)=1
\\
\\
\\0,gcd(a,n)\neq 1
\end{matrix}\right.\]

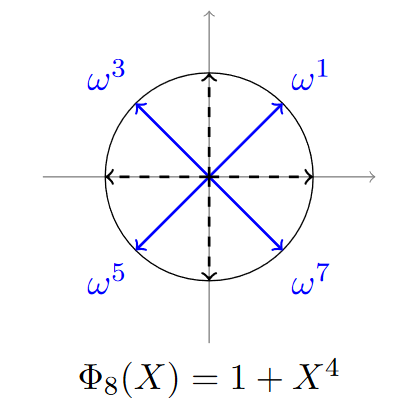
（8）全部单位根把复数平面的单位圆周(|z|=1)n等分了，构成了外接圆半径为1的正n边形的顶点，其中一个顶点为 \(x_0(1,0)\)

举例：