Linux基础命令---mysqlimport导入数据库

mysqlimport

mysqlimport指令可以用来将文本文件中的数据导入到数据库。在导入文本文件的时候，必须确保数据库中有一张表，而且他的名字和文本文件的名字是一样的。

此命令的适用范围：RedHat、RHEL、Ubuntu、CentOS、Fedora。

 

1、语法

      mysqlimport [options]  dbname  textfile1 ... 

 

2、选项参数列表

选项	说明
-？ | --help	显示帮助信息
--bind-address=ip	绑定ip
--character-sets-dir	默认的字符集目录
-i | --ignore	与replace选项相同
-c | --columns	设置字段列表
-C | --compress	在服务器和客户端之间使用压缩语句
-D | --delete	导入数据之前，删除数据库表
-f | --force	强制执行
-ignore-lines	忽略前n行
-L| --local	从客户端主机读取内容
-l | --local-tables	执行写操作之前，锁定表
-P | --port	指定端口
--protocol	指定协议
-r | --replace	如果有相同的行，那么久覆盖
-v | --verbose	显示详细过程
-V | --version	显示版本信息
-u | --users	指定用户
-p | --password	指定密码

 

3、实例

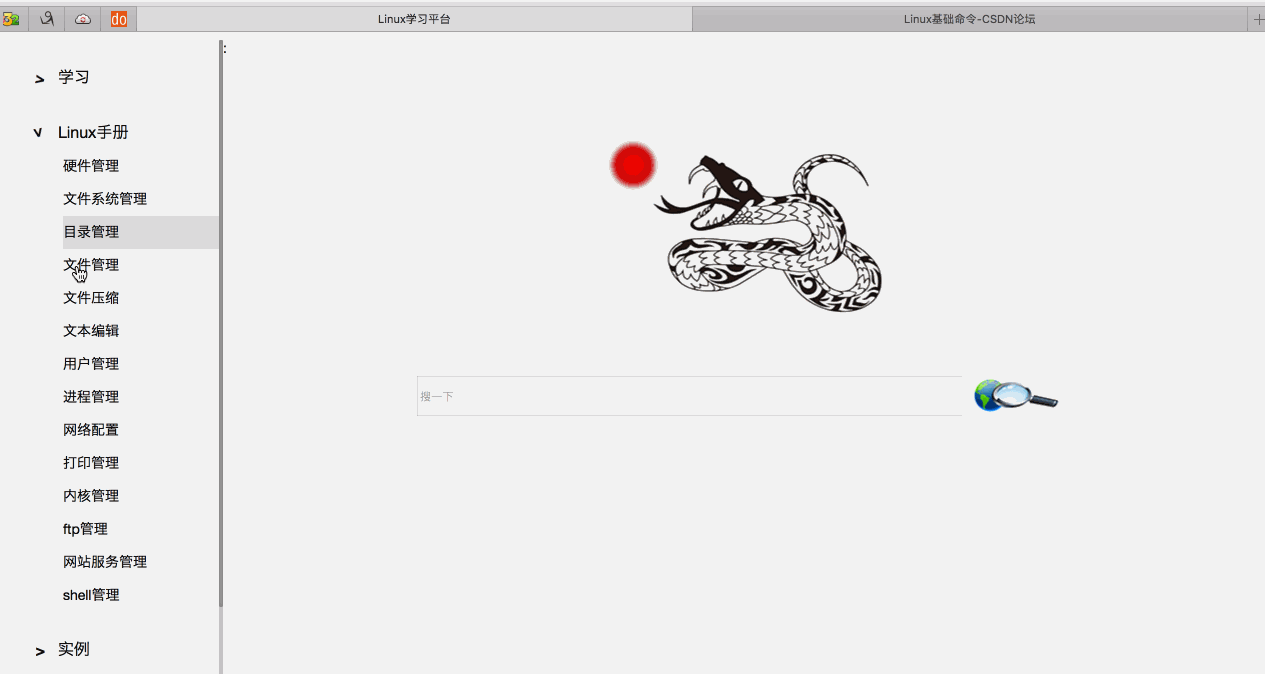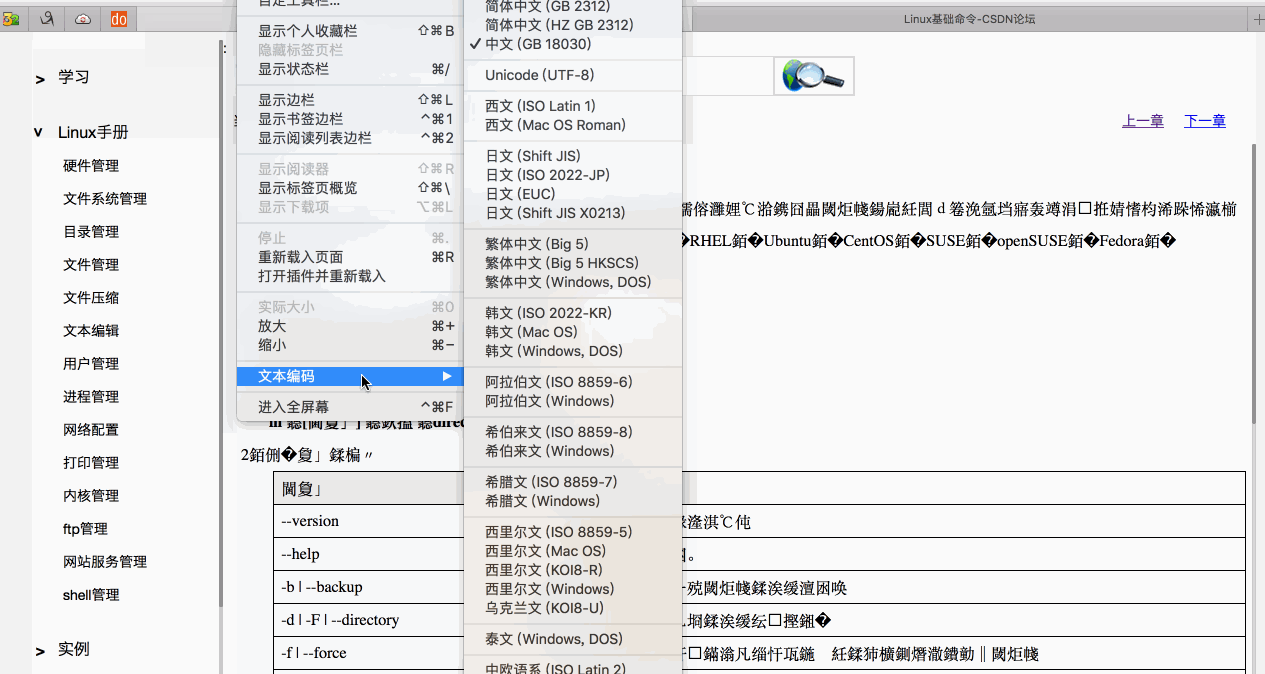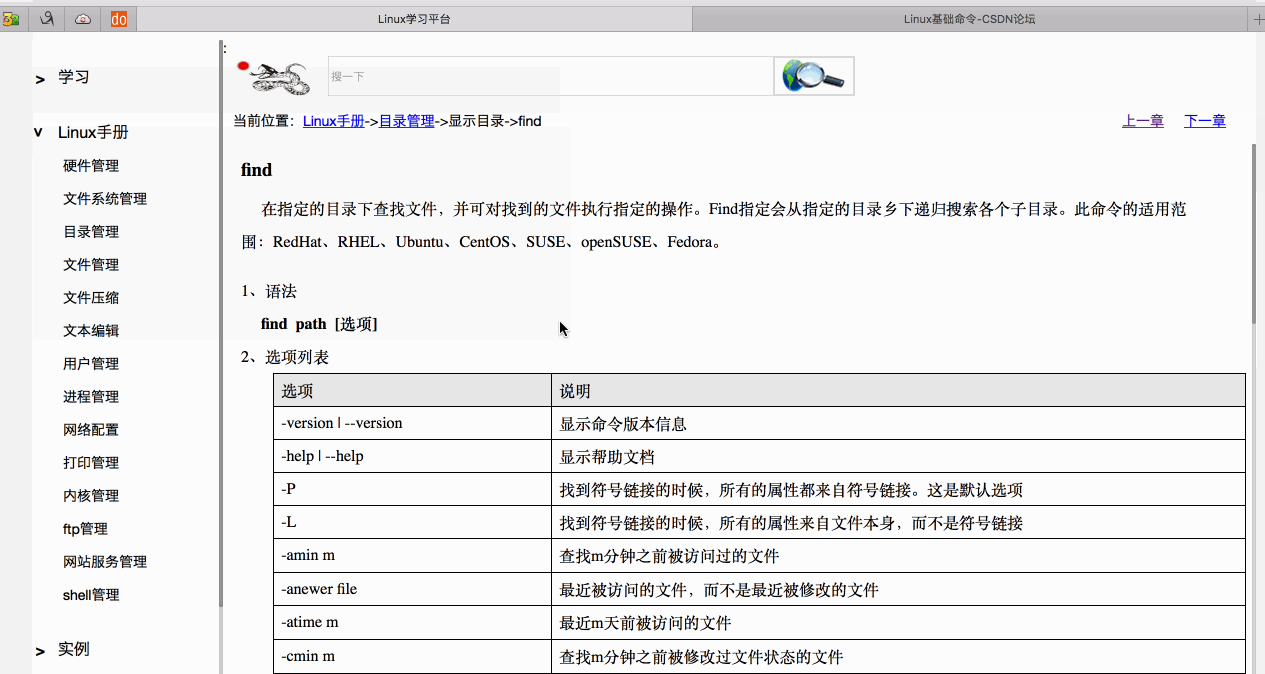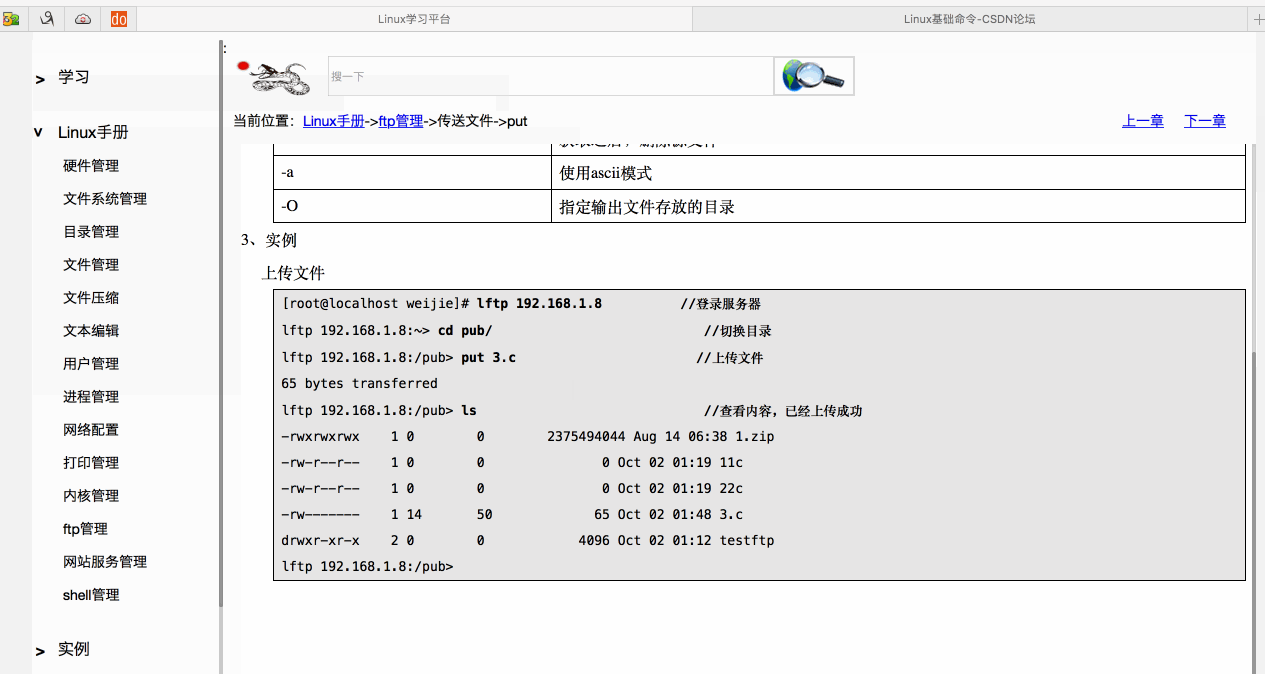
导入数据库文件

[root@localhost ~]# cat wj.txt                 //查看文本内容

1                zhangsan

2                lisi

3                wangwu

4                zhangliu

 

[root@localhost ~]#mysqlimport -v -u root -p test wj.txt          //导入文本到数据库。前提是必须有一个表，而且名字和文本文件的名字一样

Enter password: 

Connecting to localhost

Selecting database test

Loading data from SERVER file: wj.txt into wj

test.wj: Records: 4  Deleted: 0  Skipped: 0 Warnings: 0

Disconnecting from localhost 

 

[root@localhost ~]# mysql -u root -p -e 'select * from wj' test           //查看数据库中表wj的内容

Enter password: 

+----+----------+

| id | name     |

+----+----------+

|  1 | zhangsan |

|  2 | lisi     |

|  3 | wangwu   |

|  4 | zhangliu |

+----+----------+

做了一个Linux学习的平台，目前出来一个雏形，各位可以参考使用
      链接:https://pan.baidu.com/s/1GOLVU2CbpBNGtunztVpaCQ 密码:n7bk