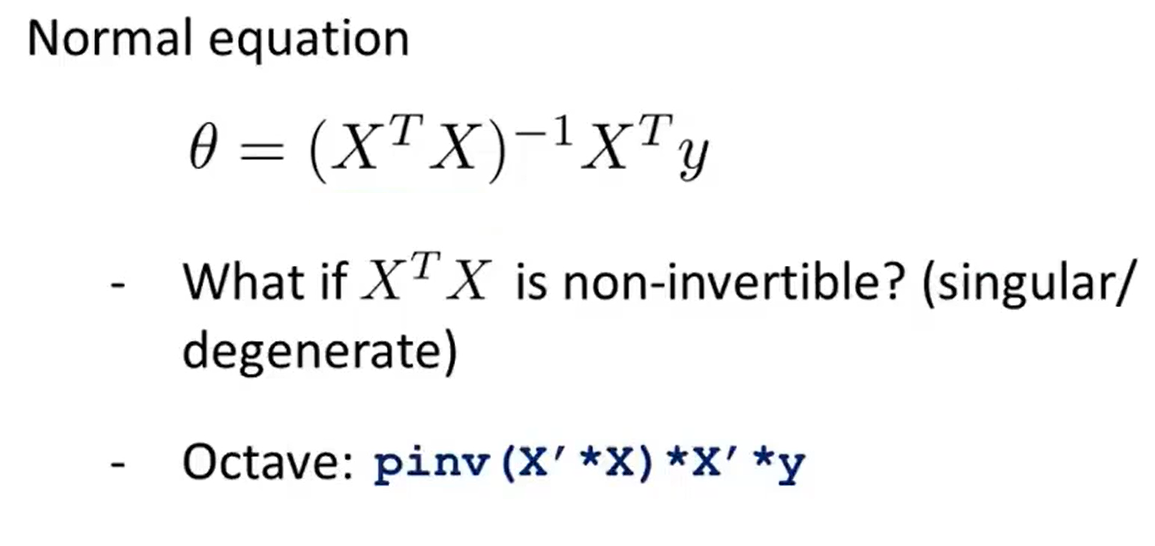Machine learning(4-Linear Regression with multiple variables )
1、Multiple features
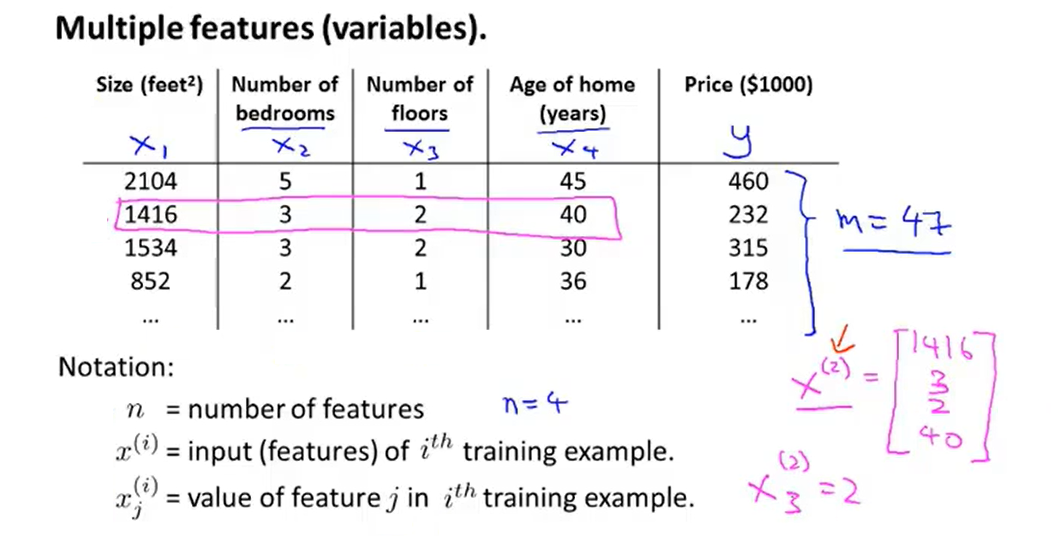
- So what the form of the hypothesis should be ?
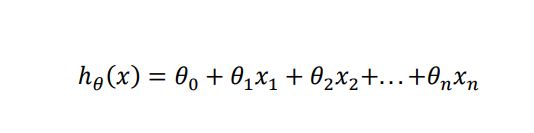
- For convenience, define x0=1
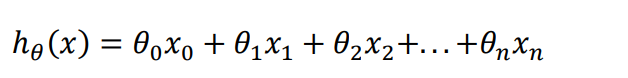
- At this time, the parameter in the model is a ( + 1)-dimensional vector, and any training instance is also a ( + 1)-dimensional vector. The dimension of the feature matrix is { ∗ ( + 1)} , so the formula can be simplified to :

2、Gradient descent for multiple variables
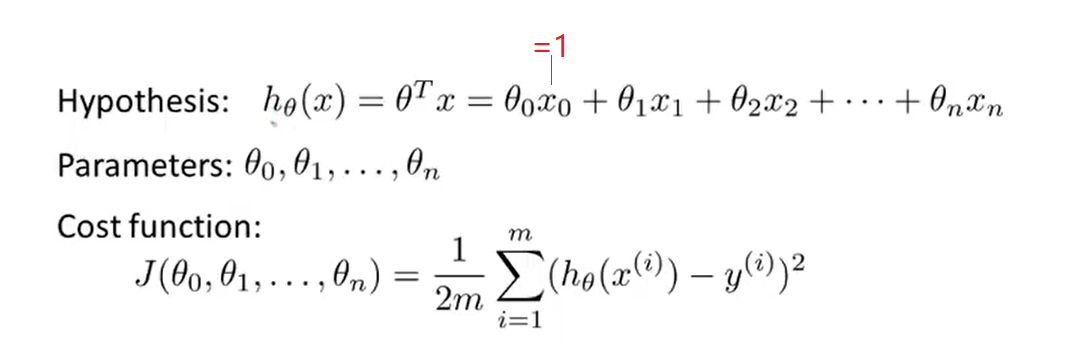
- Here is the gradient descent looks like

- Python code:
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X)
3、Gradient descent in practice I :Feature Scaling
- An idea about feature scaling(特征缩放) --- make sure features are on a similar scale and get every feature into approximately a -1≤xi≤1 range
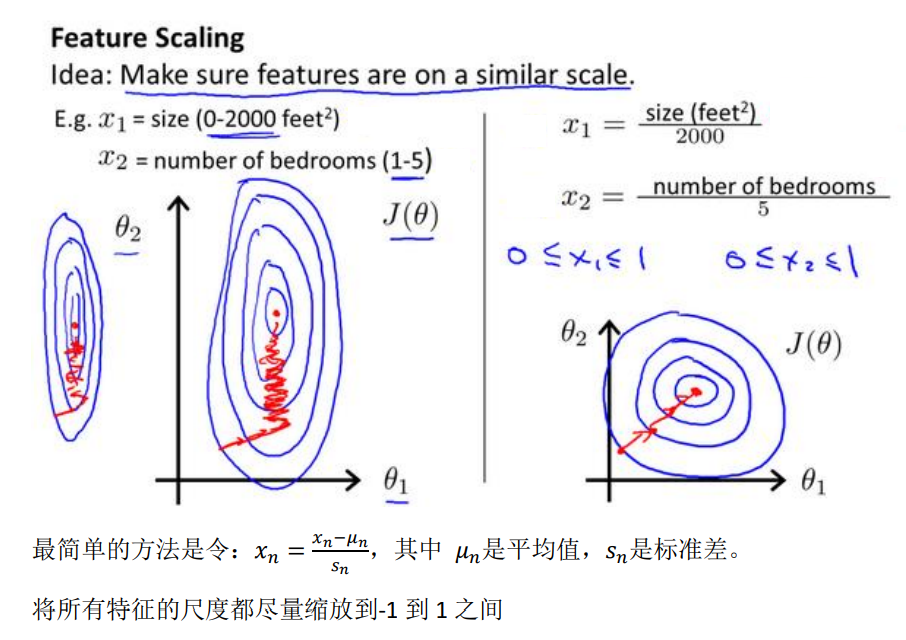
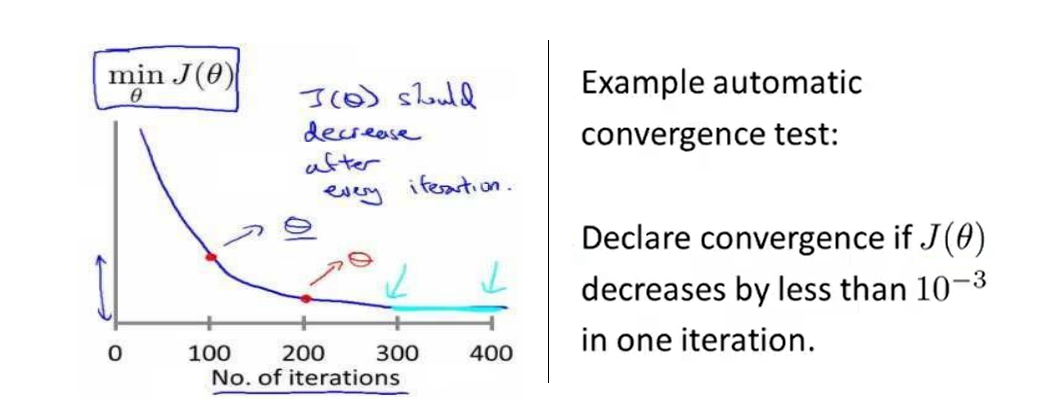
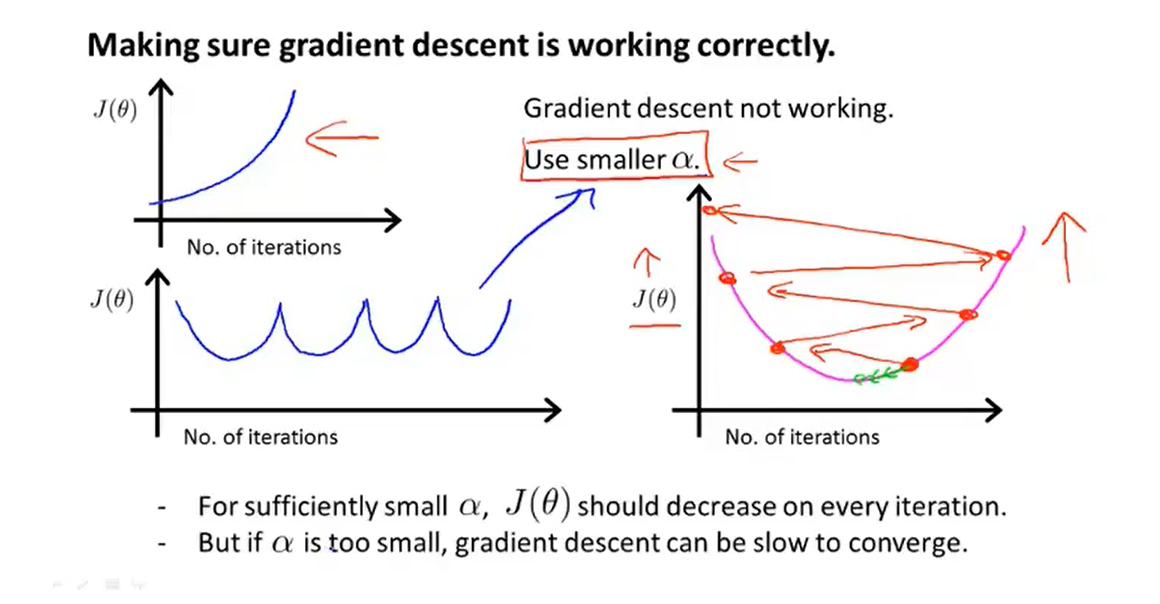
4、Gradient descent in practice II: Learning rate
5、Features and Polynomial Regression
- Housing price prediction

- Linear regression is not suitable for all data, sometimes we need a curve to fit our data, such as a quadratic model :
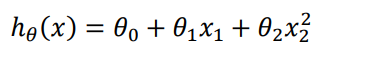
- Or maybe a cubic model :
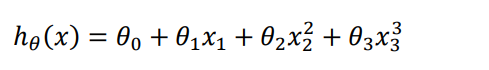
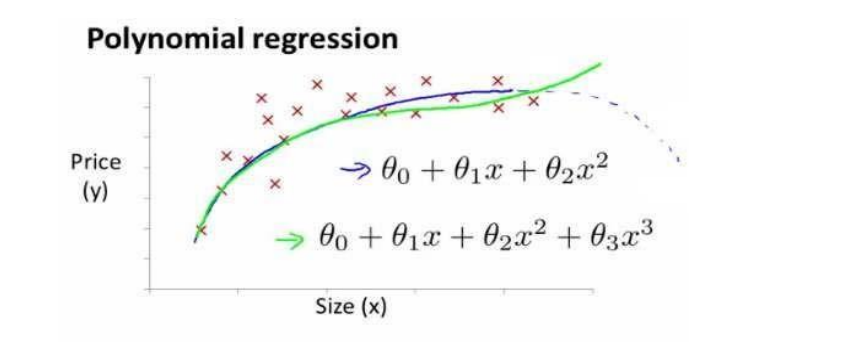
- According to the graphical characteristics of the function, we can also use :
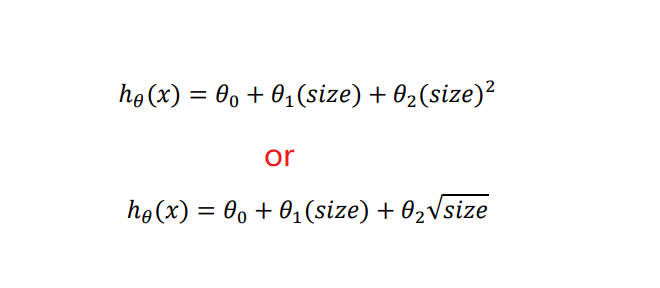
6、Normal Equation
- Normal equation : method to solve for θ analytically
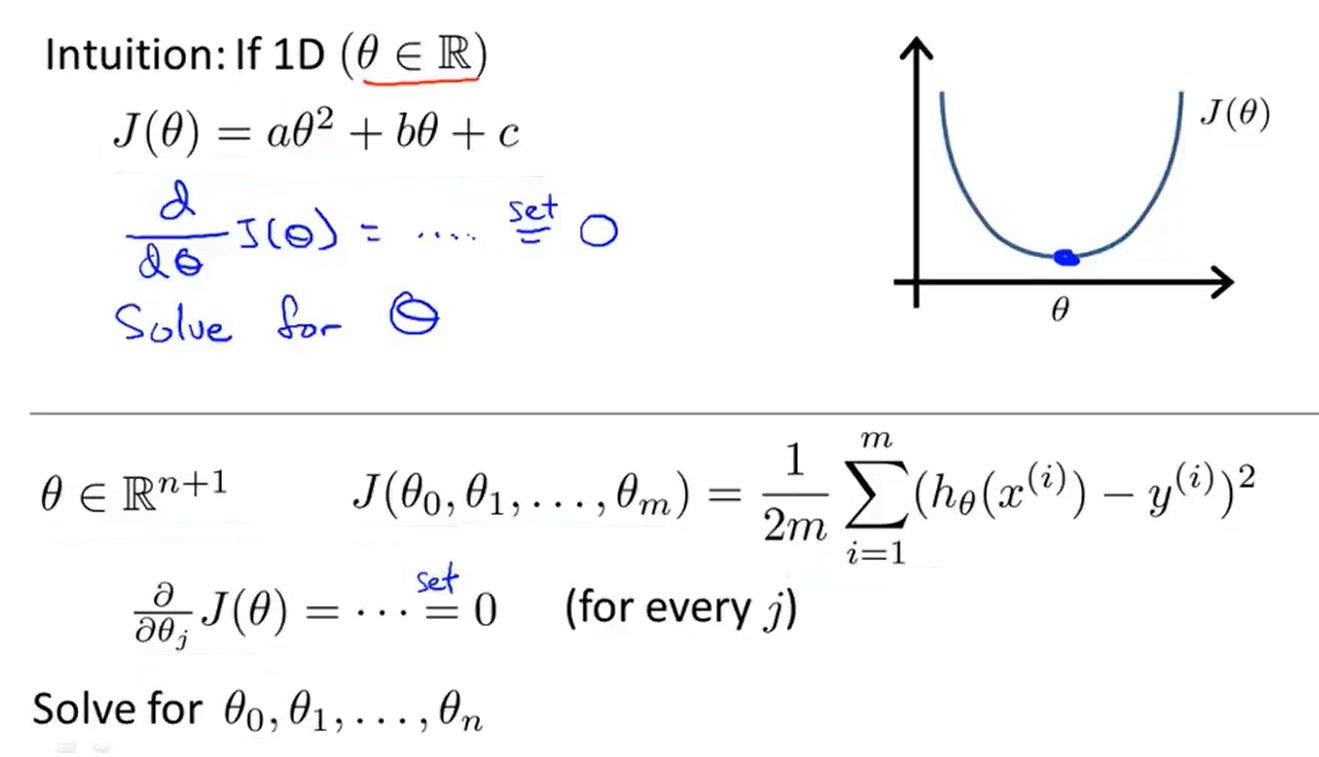
- It is too long and involved
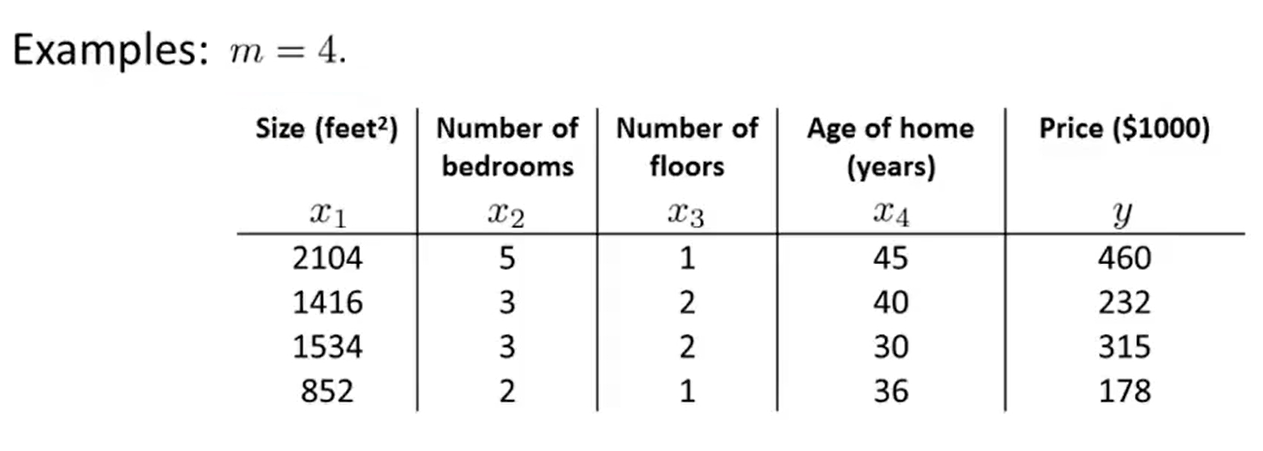
- And now,I am going to take the dataset and add an extra column
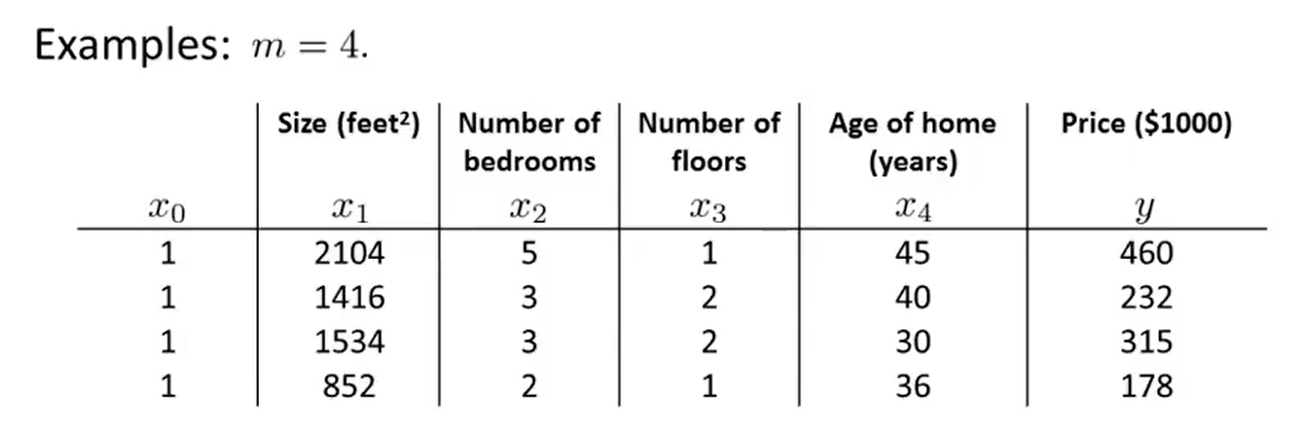
- Then construct a matrix X :

- And construct a vector y :
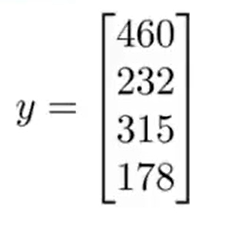
- Solve the vector using the normal equation :
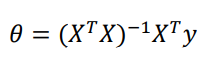
- We get :
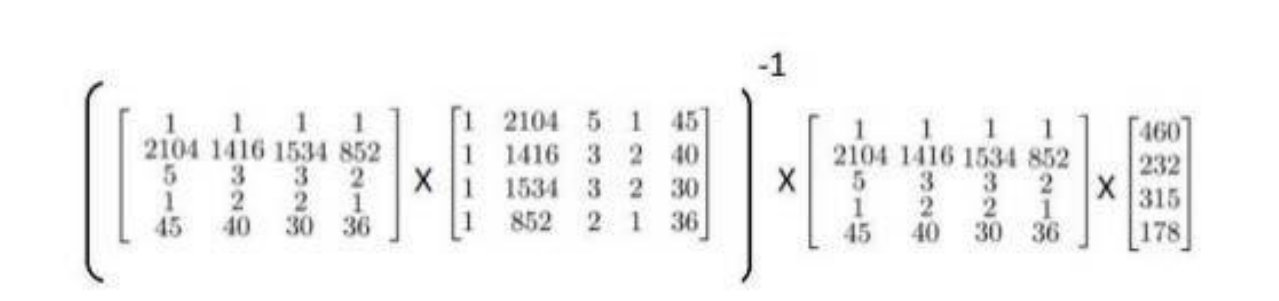
pinv(X'*X)*X'*y
- How to choose gradient descent or normal equation ?
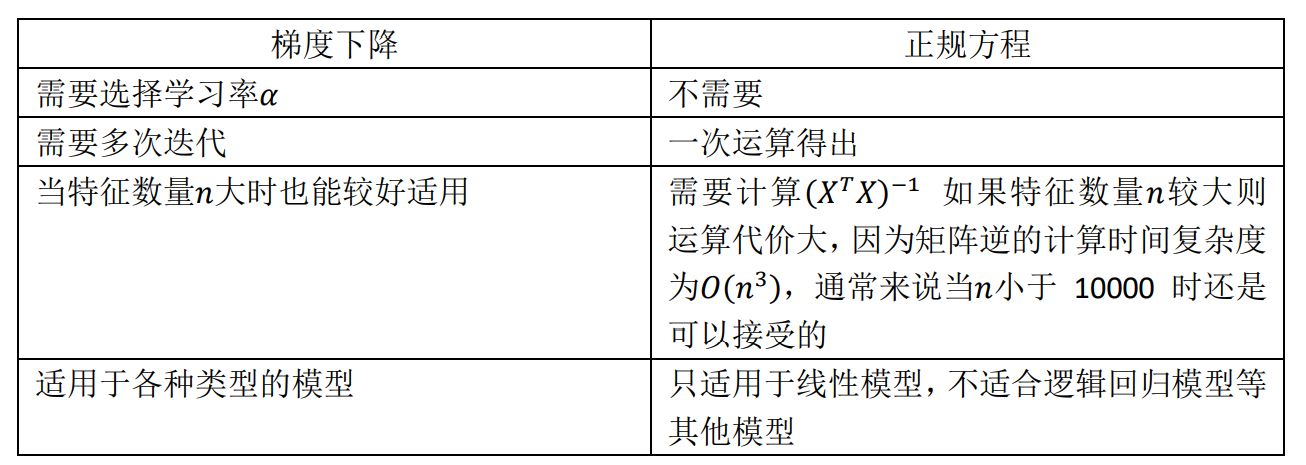
- Use python to implement Normal Equation
import numpy as np
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X 等价于 X.T.dot(X)
return theta
7、Normal Equation Non-invertibility
8、Supplement

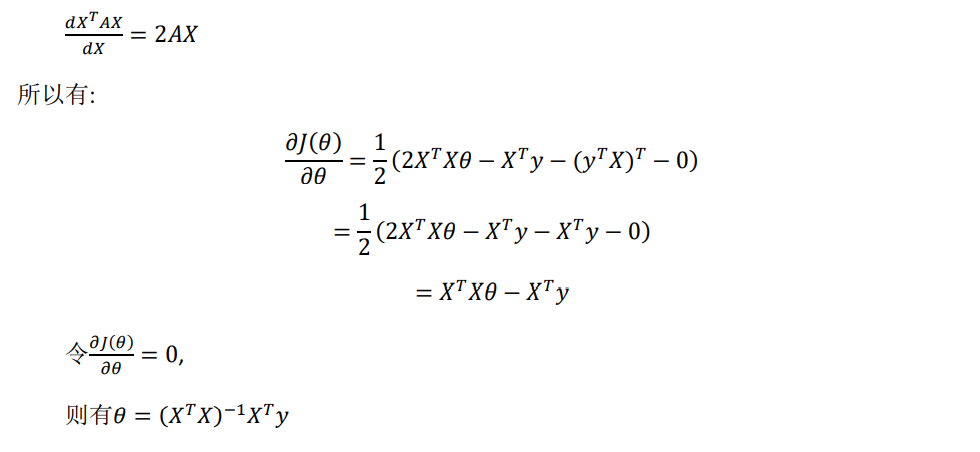
Machine learning(4-Linear Regression with multiple variables )的更多相关文章
- Machine Learning No.2: Linear Regression with Multiple Variables
1. notation: n = number of features x(i) = input (features) of ith training example = value of feat ...
- 机器学习之多变量线性回归(Linear Regression with multiple variables)
1. Multiple features(多维特征) 在机器学习之单变量线性回归(Linear Regression with One Variable)我们提到过的线性回归中,我们只有一个单一特征量 ...
- [Machine Learning] 多变量线性回归(Linear Regression with Multiple Variable)-特征缩放-正规方程
我们从上一篇博客中知道了关于单变量线性回归的相关问题,例如:什么是回归,什么是代价函数,什么是梯度下降法. 本节我们讲一下多变量线性回归.依然拿房价来举例,现在我们对房价模型增加更多的特征,例如房间数 ...
- ML:多变量线性回归(Linear Regression with Multiple Variables)
引入额外标记 xj(i) 第i个训练样本的第j个特征 x(i) 第i个训练样本对应的列向量(column vector) m 训练样本的数量 n 样本特征的数量 假设函数(hypothesis fun ...
- Machine Learning – 第2周(Linear Regression with Multiple Variables、Octave/Matlab Tutorial)
Machine Learning – Coursera Octave for Microsoft Windows GNU Octave官网 GNU Octave帮助文档 (有900页的pdf版本) O ...
- Andrew Ng Machine Learning 专题【Linear Regression】
此文是斯坦福大学,机器学习界 superstar - Andrew Ng 所开设的 Coursera 课程:Machine Learning 的课程笔记. 力求简洁,仅代表本人观点,不足之处希望大家探 ...
- CheeseZH: Stanford University: Machine Learning Ex5:Regularized Linear Regression and Bias v.s. Variance
源码:https://github.com/cheesezhe/Coursera-Machine-Learning-Exercise/tree/master/ex5 Introduction: In ...
- 机器学习(三)--------多变量线性回归(Linear Regression with Multiple Variables)
机器学习(三)--------多变量线性回归(Linear Regression with Multiple Variables) 同样是预测房价问题 如果有多个特征值 那么这种情况下 假设h表示 ...
- Linear regression with multiple variables(多特征的线型回归)算法实例_梯度下降解法(Gradient DesentMulti)以及正规方程解法(Normal Equation)
,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, , ...
- 机器学习 (二) 多变量线性回归 Linear Regression with Multiple Variables
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...
随机推荐
- vuex前端工程化之动态导入文件--require.context( )
随着项目的复杂,文件结构越来越多,Store中modules中的文件也越来越多,如果一个一个加载是不是很麻烦呢? 先看一个项目中store项目结构: 过去都是通过import分别引入文件: 1 imp ...
- PHP中的PDO操作学习(四)查询结构集
关于 PDO 的最后一篇文章,我们就以查询结果集的操作为结束.在数据库的操作中,查询往往占的比例非常高.在日常的开发中,大部分的业务都是读多写少型的业务,所以掌握好查询相关的操作是我们学习的重要内容. ...
- dede图片集关联的数据库用表:
如果在本地的环境中,安装目录不在根目录,搬到外网上的时候,就需要对数据库里的图片路径数据进行字段替换: dede图片集关联的数据库用表:1.dede_addonimages 2.dede_arctin ...
- Nginx系列(9)- Nginx常用命令
Linux # 命令需要在Nginx的sbin目录下执行 cd /usr/local/nginx/sbin/ ./nginx #启动./nginx -s stop #停止 ./nginx -s qui ...
- Docker系列(13)- 部署es+kibana
部署elasticsearch # es 暴露的端口很多 # es 十分的消耗内存 # es 的数据一帮需要放置到安全目录!通过挂载实现 # DockerHub上安装文档,其中 --net somen ...
- PHP 相对路径转换为绝对路径 realpath
* 相对路径 -> 绝对路径 realpath <?php /** * @param string $in_rel: relative directory * @param string ...
- 为什么Charles中的中文展示成数字、英文字符串
在使用charles抓包时,可能非看到如下图的字符串: 为什么会出现这样的字符串? 我们看到的汉字.字母,对电脑来说并不长这样,而是用二进制表示的(显然--),为了统一标准,老外发明了"字符 ...
- Python Type Hints(类型提示)
在做自动化测试的时候,改进测试框架,类型提示会让你写代码时更加流程,当你在一个模块定义了类型,而其他模块没有提示的时候,是相当不方便.
- 将可执行程序设为linux服务启动
将可执行程序设为linux服务启动 如何将我们自己的程序设为linux的一个服务程序,并实现开机启动,需要经过如下三步: 1 把可执行程序放在一个linux系统可以找到的地方. ...
- Nresource服务之接口缓存化
1. 背景 Nresource服务日均4.5亿流量,考虑到未来流量急增场景,我们打算对大流量接口进行缓存化处理:根据服务管理平台数据统计显示getUsableResoureCount接口调用量很大,接 ...