[leetcode] 48. 旋转图像(Java)(模拟)

48. 旋转图像

模拟题，其实挺不喜欢做模拟题的。。。

其实这题一层一层的转就好了，外层转完里层再转，其实就是可重叠的子问题了。

转的时候呢，一个数一个数的转，一个数带动四个数。如图所示，2这个数应该怎么转：

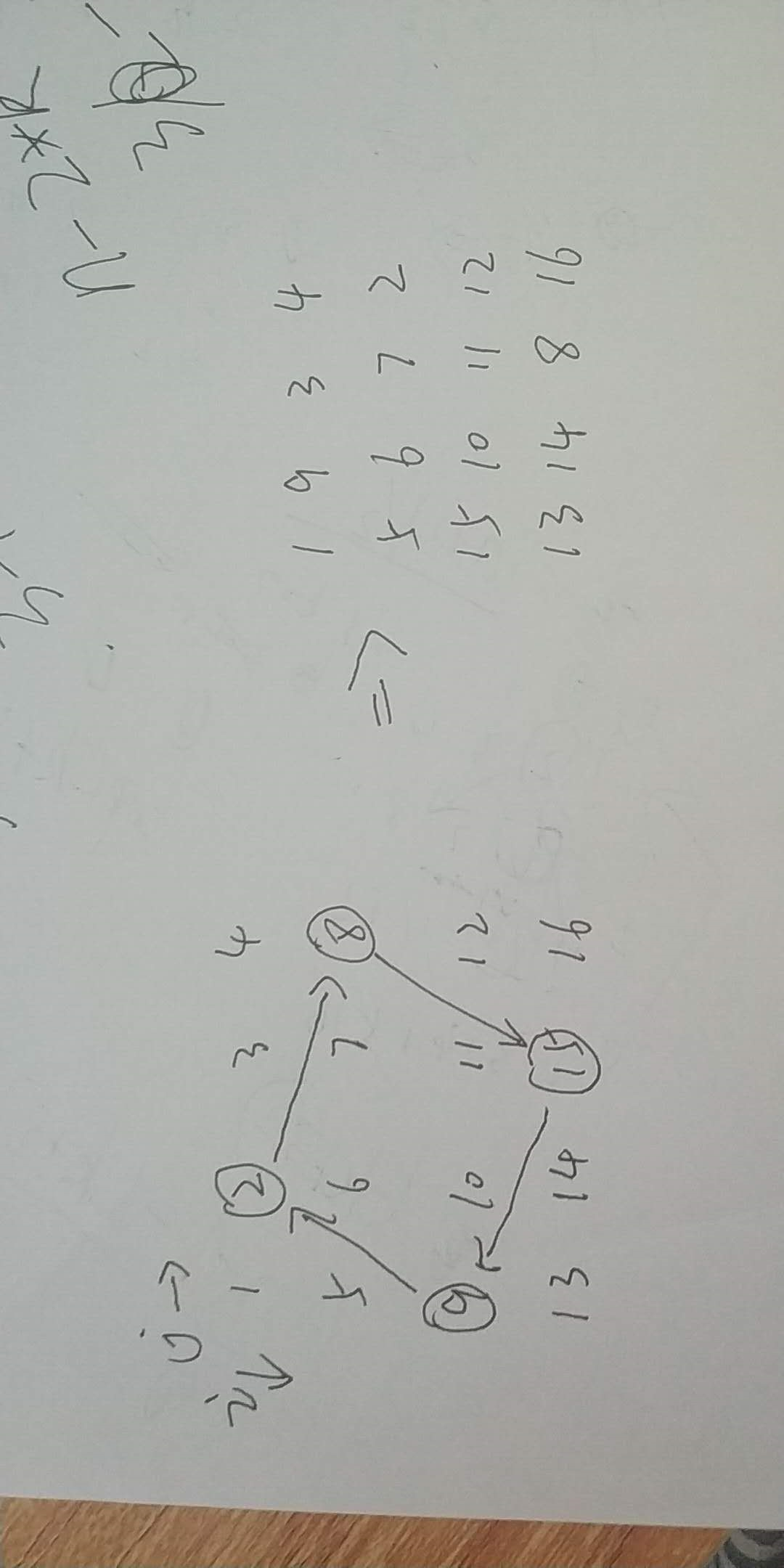
难点就是如何用坐标表示出来相对位置，写坐标的时候思路一定要清晰啊！

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int k = 0; k < n / 2; k++) {
            for (int i = 0; i < ((n - 2 * k) - 1); i++) {
                int tmp = matrix[k][k + i];
                matrix[k][k + i] = matrix[n - 1 - (k + i)][k];
                matrix[n - 1 - (k + i)][k] = matrix[n - 1 - k][n - 1 - (k + i)];
                matrix[n - 1 - k][n - 1 - (k + i)] = matrix[k + i][n - 1 - k];
                matrix[k + i][n - 1 - k] = tmp;
            }
        }
    }
}