【LeetCode】883. Projection Area of 3D Shapes 解题报告（Python）

作者： 负雪明烛
id： fuxuemingzhu
个人博客： http://fuxuemingzhu.cn/

---

目录

• • 题目描述
  • 题目大意
  • 解题方法
  • • 数学计算
  • 日期

题目地址：https://leetcode.com/problems/projection-area-of-3d-shapes/description/

题目描述

On a N * N grid, we place some 1 * 1 * 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).

Now we view the projection of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3 dimensional figure to a 2 dimensional plane.

Here, we are viewing the “shadow” when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

Example 1:

Input: [[2]]
Output: 5

Example 2:

Input: [[1,2],[3,4]]
Output: 17
Explanation:
Here are the three projections ("shadows") of the shape made with each axis-aligned plane.

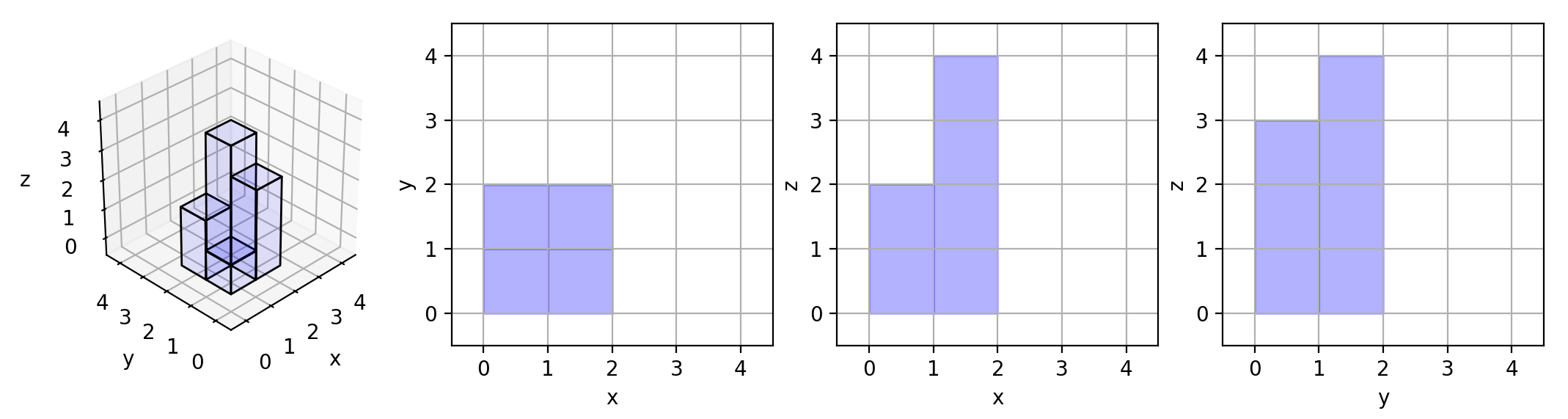
Example 3:

Input: [[1,0],[0,2]]
Output: 8

Example 4:

Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 14

Example 5:

Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 21

Note:

1. 1 <= grid.length = grid[0].length <= 50
2. 0 <= grid[i][j] <= 50

题目大意

给出了一个方阵，方阵里面的数值是柱子的高度，求三视图所有的阴影部分的面积。

解题方法

数学计算

稍微缕一下就能明白，俯视图投影就是不为0的柱子的个数，主视图、侧视图是当前视图柱子的最高值求和。

代码如下：

class Solution(object):
    def projectionArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        top, front, side = 0, 0, 0
        n = len(grid)
        for i in range(n):
            x, y = 0, 0
            for j in range(n):
                if grid[i][j] != 0:
                    top += 1
                x = max(x, grid[i][j])
                y = max(y, grid[j][i])
            front += x
            side += y
        return top + front + side

也可以三视图分别进行计算，似乎更清晰明了。

class Solution:
    def projectionArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        M, N = len(grid), len(grid[0])
        rowMax, colMax = [0] * M, [0] * N
        xy = sum(0 if grid[i][j] == 0 else 1 for i in range(M) for j in range(N))
        xz = sum(list(map(max, grid)))
        yz = sum(list(map(max, [[grid[i][j] for i in range(M)] for j in range(N)])))
        return xy + xz + yz

日期

2018 年 8 月 16 日 —— 一个月不写题，竟然啥都不会了。。加油！
2018 年 11 月 5 日 —— 打了羽毛球，有点累