python 之爬虫基本流程

python 之爬虫基本流程

一 用户获取网络数据的方式：

方式1：浏览器提交请求--->下载网页代码--->解析成页面

方式2：模拟浏览器发送请求(获取网页代码)->提取有用的数据->存放于数据库或文件中爬虫要做的就是方式2；

1、发起请求

使用http库向目标站点发起请求，即发送一个Request

Request包含：请求头、请求体等

Request模块缺陷：不能执行JS 和CSS 代码

2、获取响应内容

如果服务器能正常响应，则会得到一个Response

Response包含：html，json，图片，视频等

3、解析内容

解析html数据：正则表达式（RE模块），第三方解析库如Beautifulsoup，pyquery等

解析json数据：json模块

解析二进制数据:以wb的方式写入文件

4、保存数据

数据库（MySQL，Mongdb、Redis）

文件

三、http协议 请求与响应



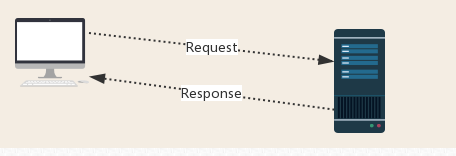
Request：用户将自己的信息通过浏览器（socket client）发送给服务器（socket server）

Response：服务器接收请求，分析用户发来的请求信息，然后返回数据（返回的数据中可能包含其他链接，如：图片，js，css等）

ps：浏览器在接收Response后，会解析其内容来显示给用户，而爬虫程序在模拟浏览器发送请求然后接收Response后，是要提取其中的有用数据

四、 request

1、请求方式：

常见的请求方式：GET / POST

2、请求的URL

url全球统一资源定位符，用来定义互联网上一个唯一的资源 例如：一张图片、一个文件、一段视频都可以用url唯一确定

url编码

https://www.baidu.com/s?wd=图片

图片会被编码（看示例代码）

网页的加载过程是：

加载一个网页，通常都是先加载document文档，

在解析document文档的时候，遇到链接，则针对超链接发起下载图片的请求

3、请求头

User-agent：请求头中如果没有user-agent客户端配置，服务端可能将你当做一个非法用户host；

cookies：cookie用来保存登录信息

注意： 一般做爬虫都会加上请求头

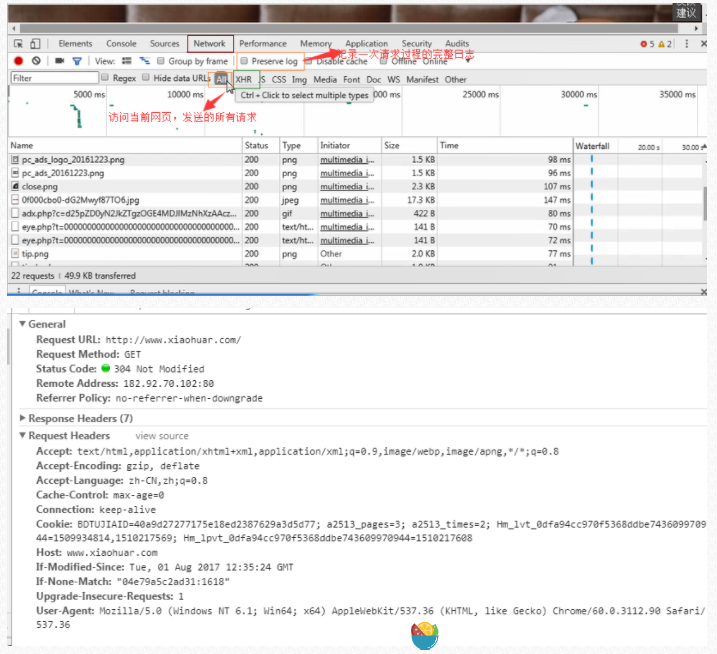
请求头需要注意的参数：

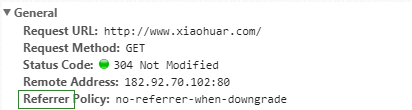
（1）Referrer：访问源至哪里来（一些大型网站，会通过Referrer 做防盗链策略；所有爬虫也要注意模拟）

（2）User-Agent:访问的浏览器（要加上否则会被当成爬虫程序）

（3）cookie：请求头注意携带

4、请求体

请求体

如果是get方式，请求体没有内容 （get请求的请求体放在 url后面参数中，直接能看到）

如果是post方式，请求体是format data

ps：

1、登录窗口，文件上传等，信息都会被附加到请求体内

2、登录，输入错误的用户名密码，然后提交，就可以看到post，正确登录后页面通常会跳转，无法捕捉到post

五、 响应Response

1、响应状态码

200：代表成功

301：代表跳转

404：文件不存在

403：无权限访问

502：服务器错误

2、respone header

响应头需要注意的参数：

（1）Set-Cookie:BDSVRTM=0; path=/：可能有多个，是来告诉浏览器，把cookie保存下来

（2）Content-Location：服务端响应头中包含Location返回浏览器之后，浏览器就会重新访问另一个页面

3、preview就是网页源代码

JSO数据

如网页html，图片

二进制数据等