Project Euler 106：Special subset sums: meta-testing 特殊的子集和：元检验

Special subset sums: meta-testing

Let S(A) represent the sum of elements in set A of size n. We shall call it a special sum set if for any two non-empty disjoint subsets, B and C, the following properties are true:

1. S(B) ≠ S(C); that is, sums of subsets cannot be equal.
2. If B contains more elements than C then S(B) > S(C).

For this problem we shall assume that a given set contains n strictly increasing elements and it already satisfies the second rule.

Surprisingly, out of the 25 possible subset pairs that can be obtained from a set for which n = 4, only 1 of these pairs need to be tested for equality (first rule). Similarly, when n = 7, only 70 out of the 966 subset pairs need to be tested.

For n = 12, how many of the 261625 subset pairs that can be obtained need to be tested for equality?

NOTE: This problem is related to Problem 103 and Problem 105.

---

特殊的子集和：元检验

记S(A)是大小为n的集合A中所有元素的和。若任取A的任意两个非空且不相交的子集B和C都满足下列条件，我们称A是一个特殊的和集：

1. S(B) ≠ S(C)；也就是说，任意子集的和不相同。
2. 如果B中的元素比C多，则S(B) > S(C)。

在这个问题中我们假定集合中包含有n个严格单调递增的元素，并且已知其满足第二个条件。

令人惊奇的是，当n = 4时，在所有可能的25组子集对中只有1组需要检验子集和是否相等（第一个条件）。同样地，当n = 7时，在所有可能的966组子集对中只有70组需要检验。

当n = 12时，在所有可能的261625组子集对中有多少组需要检验？

注意：此题和第103题及第105题有关。

解题

首先 想说的是语文差，题目没理解，搞了好久。

注意几点：

1.这里的集合和不一定是特殊子集

2.这个集合元素一定是严格递增的

3.集合是已经满足第二个条件，解题中不需要判断

4.求的是子集对可能相等的个数

4.1子集对，两个子集也一定是不相交的

4.2“需要检验”的意思是，不需要检验的子集对一定不相等，“需要检验”的子集对可能相等，注意这里面的可能  ，它也可能不相等，可以理解为：要求的是最大的个数

当 1 2 3 条都正确理解到的时候：n个数的集合只要是任意n个数的递增序列就好了，如：1、2、3、4,、、、、、、n

第4条：求子集对可能相等的个数

什么情况下两个子集B、C内元素的和是相等的？

注意：集合A是严格递增的，则子集B、C也一定是严格递增的

子集B、C元素和一定不相等的情况：

1.集合B、C的元素个数不相等

2.集合B的最小值 > 集合C的最大值

反过来

子集B、C元素和可能相等的情况：

1.集合B、C的元素个数相等 并且 B中的元素有大于C中的元素的，C中的元素有大于B中的元素的

根据上面就可解

Java

package Level4;
import java.util.ArrayList;
import java.util.Arrays;

public class PE0106{

    public static void run(){
        int A[] = { 1,2,3,4,5,6,7,8,9,10,11,12};
//        int A[] = {1219 ,1183, 1182, 1115, 1035, 1186, 591, 1197, 1167, 887, 1184, 1175};
        Arrays.sort(A);
        meta_testing(A);

    }
    public static void meta_testing(int[] a){
        // 所有的子集
        ArrayList<ArrayList<Integer>> sets = MakeSubsets(a);
        int size = sets.size();
        int count_equal = 0;
        int count_sets = 0;
        System.out.println("子集总数量："+size);
        for(int i=0;i<size;i++){
            ArrayList<Integer> set1 = sets.get(i);
            for(int j=i+1;j<size;j++){
                ArrayList<Integer> set2 = sets.get(j);
                //不相交
                if(!isDisjoint(set1,set2) ){
                    count_sets++;
                    if(set1.size() == set2.size()){
                        int s = 0;
                        int t = 0;
                        for(int k = 0;k<set1.size();k++){
                            if(set1.get(k) > set2.get(k))
                                s = 1;
                            if(set1.get(k) < set2.get(k))
                                t = 1;

                        }
                        if(s == 1 && t == 1)
                            count_equal++;

                    }

                }
            }
        }
        System.out.println("子集对数量："+count_sets);
        System.out.println("可能相等的子集数量："+count_equal);
    }

    // 两个子集元素是否相交 true 相交 false 不相交
    public static boolean isDisjoint(ArrayList<Integer> set1,ArrayList<Integer> set2){
        int size1 = set1.size();
        int size2 = set2.size();
        ArrayList<Integer> set = new ArrayList<Integer>();
        for(int i=0;i<size1;i++){
            int element = set1.get(i);
            if(set.contains(element))
                return true;
            else
                set.add(element);
        }
        for(int i=0;i<size2;i++){
            int element = set2.get(i);
            if(set.contains(element))
                return true;
            else
                set.add(element);
        }
        set.clear();
        return false;

    }

    // 求出所有的子集
    public static ArrayList<ArrayList<Integer>> MakeSubsets(int a[]){
        ArrayList<ArrayList<Integer>> sets = new ArrayList<ArrayList<Integer>>();
        for(int i=1;i< (int) Math.pow(2,a.length);i++){
            ArrayList<Integer> set = MakeSubset(a,i);
            sets.add(set);
        }
        return sets;

    }
    // 求出子集
        // 利用 和  1 进行与运算 并移位
        //  001001 相当于根据 1 所在的位置取 第 2 第 5的位置对应的数
        // &000001
        //----------
        //       1 取出该位置对应的数
        // 下面右移一位后
        //  000100
        // 下面同理了
    public static ArrayList<Integer> MakeSubset(int[] a,int m){
        ArrayList<Integer> set = new ArrayList<Integer>();
        for(int i=0;i<a.length ;i++){
            if( m>0 &&(m&1)==1){
                set.add(a[i]);
            }
            m =m>>1;
        }
        return set;
    }
    public static void main(String[] args){
        long t0 = System.currentTimeMillis();
        run();
        long t1 = System.currentTimeMillis();
        long t = t1 - t0;
        System.out.println("running time="+t/1000+"s"+t%1000+"ms");
    }
}

Java Code

子集总数量：4095
子集对数量：261625
可能相等的子集数量：21384
running time=3s496ms

Python

# coding=gbk
import itertools

se=set(range(1,13))
c=0
for i in xrange(2,len(se)):
        for m in itertools.combinations(se,i):
                for n in itertools.combinations(se-set(m),i):
                        t=0
                        for k in range(len(m)):
                            if m[k]>n[k]:
                                t=1
                        s=0
                        for k in range(len(m)):
                            if m[k]<n[k]:
                                s=1
                        if s==1 and t==1:
                            c+=1
print c/2.

Mathblog 中直接求出答案，所有的子集对数量比较好求，至于后来用到了卡特兰数，问题没有过多的讲解，我也不知道为什么。

答案=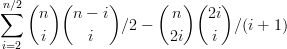 

题解中看到的解答：

# coding=gbk
import itertools

def C(n,k):
    result = 1
    for i in range(k):
        result *= n - i
        result /= i + 1
    return result

def Catalan(n):
    return C(2 * n, n) / (n + 1)

def e106meta(n):
    result = 0
    for k1 in range(1,n):
        for k2 in range(1,min(k1,n-k1)+1):
            x = C(n,k1)*C(n-k1,k2)
            if k1 == k2:
                x /= 2
            result += x
    return result

def e106(n):
    result = 0
    for k in range(2,n/2 + 1):
        result += C(n,2*k)*(C(2*k,k)/2 - Catalan(k))
    return result

if __name__ == '__main__':
    assert e106(7) == 70
    print e106(12)