V-rep学习笔记：机器人逆运动学数值解法（Damped Least Squares / Levenberg-Marquardt Method）

　　The damped least squares method is also called the Levenberg-Marquardt method. Levenberg-Marquardt算法是最优化算法中的一种。它是使用最广泛的非线性最小二乘算法，具有梯度法和牛顿法的优点。当λ很小时，步长等于牛顿法步长，当λ很大时，步长约等于梯度下降法的步长。

　　The damped least squares method can be theoretically justified as follows.Rather than just finding the minimum vector ∆θ that gives a best solution to equation （pseudo inverse method就是求的极小范数解）, we find the value of ∆θ that minimizes the quantity：

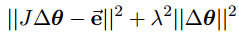
where λ ∈ R is a non-zero damping constant. This is equivalent to minimizing the quantity：

The corresponding normal equation is（根据矩阵论简明教程P83 最小二乘问题：设A∈R^m×n，b∈R^m. 若x₀∈Rⁿ是Ax=b的最小二乘解，则x₀是方程组A^TAx=A^Tb的解，称该式为Ax=b的法方程组.）

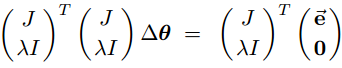
This can be equivalently rewritten as：

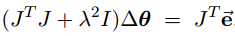
It can be shown that J^TJ + λ²I is non-singular when λ is appropriate（选取适当的参数λ可以保证矩阵J^TJ + λ²I非奇异）. Thus, the damped least squares solution is equal to：

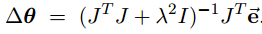
Now J^TJ  is an n × n matrix, where n is the number of degrees of freedom. It is easy to find that (J^TJ + λ²I)⁻¹J^T= J^T (JJ^T + λ²I)⁻¹(等式两边同乘(J^TJ + λ²I)进行恒等变形). Thus：

The advantage of the equation is that the matrix being inverted is only m×m where m = 3k is the dimension of the space of target positions, and m is often much less than n. Additionally, the equation can be computed without needing to carry out the matrix inversion, instead row operations can find f such that (JJ^T + λ²I) f = e and then J^Tf is the solution. The damping constant depends on the details of the multibody and the target positions and must be chosen carefully to make equation numerically stable. The damping constant should large enough so that the solutions for ∆θ are well-behaved near singularities, but if it is chosen too large, then the convergence rate is too slow.

　　以平面二连杆机构为例，使用同样的V-rep模型，将目标点放置在接近机构奇异位置处，使用DLS方法求逆解。在下面的Python程序中关节角初始值就给在奇异点上，可以看出最终DLS算法还是能收敛，而pseudo inverse方法在奇异点处就无法收敛。The damped least squares method avoids many of the pseudo inverse method’s problems with singularities and can give a numerically stable method of selecting ∆θ

import vrep             #V-rep library
import sys
import time
import math
import numpy as np

# Starts a communication thread with the server (i.e. V-REP).
clientID=vrep.simxStart('127.0.0.1', 20001, True, True, 5000, 5)

# clientID: the client ID, or -1 if the connection to the server was not possible
if clientID!=-1:  #check if client connection successful
    print 'Connected to remote API server'
else:
    print 'Connection not successful'
    sys.exit('Could not connect')    # Exit from Python

# Retrieves an object handle based on its name.
errorCode,J1_handle = vrep.simxGetObjectHandle(clientID,'j1',vrep.simx_opmode_oneshot_wait)
errorCode,J2_handle = vrep.simxGetObjectHandle(clientID,'j2',vrep.simx_opmode_oneshot_wait)
errorCode,target_handle = vrep.simxGetObjectHandle(clientID,'target',vrep.simx_opmode_oneshot_wait)
errorCode,consoleHandle = vrep.simxAuxiliaryConsoleOpen(clientID,'info',5,1+4,None,None,None,None,vrep.simx_opmode_oneshot_wait)

uiHandle = -1
errorCode,uiHandle = vrep.simxGetUIHandle(clientID,"UI", vrep.simx_opmode_oneshot_wait)
buttonEventID = -1
err,buttonEventID,aux = vrep.simxGetUIEventButton(clientID,uiHandle,vrep.simx_opmode_streaming)

L1 = 0.5        # link length
L2 = 0.5
lamda = 0.2     # damping constant
stol = 1e-2     # tolerance
nm = 100        # initial error
count = 0       # iteration count
ilimit = 1000   # maximum iteration

# initial joint value
# note that workspace-boundary singularities occur when q2 approach 0 or 180 degree
q = np.array([0,0])   

while True:
    retcode, target_pos = vrep.simxGetObjectPosition(clientID, target_handle, -1, vrep.simx_opmode_streaming)

    if(nm > stol):
        vrep.simxAuxiliaryConsolePrint(clientID, consoleHandle, None, vrep.simx_opmode_oneshot_wait) # "None" to clear the console window

        x = np.array([L1*math.cos(q[0])+L2*math.cos(q[0]+q[1]), L1*math.sin(q[0])+L2*math.sin(q[0]+q[1])])
        error = np.array([target_pos[0],target_pos[1]]) - x

        J = np.array([[-L1*math.sin(q[0])-L2*math.sin(q[0]+q[1]), -L2*math.sin(q[0]+q[1])],\
                      [L1*math.cos(q[0])+L2*math.cos(q[0]+q[1]), L2*math.cos(q[0]+q[1])]])

        f = np.linalg.solve(J.dot(J.transpose())+lamda**2*np.identity(2), error)

        dq = np.dot(J.transpose(), f)
        q = q + dq

        nm = np.linalg.norm(error)

        count = count + 1
        if count > ilimit:
            vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,"Solution wouldn't converge\r\n",vrep.simx_opmode_oneshot_wait)
        vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,'q1:'+str(q[0]*180/math.pi)+' q2:'+str(q[1]*180/math.pi)+'\r\n',vrep.simx_opmode_oneshot_wait)
        vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,str(count)+' iterations'+'  err:'+str(nm)+'\r\n',vrep.simx_opmode_oneshot_wait)   

    err, buttonEventID, aux = vrep.simxGetUIEventButton(clientID,uiHandle,vrep.simx_opmode_buffer)
    if ((err==vrep.simx_return_ok) and (buttonEventID == 1)):
        '''A button was pressed/edited/changed. React to it here!'''
        vrep.simxSetJointPosition(clientID,J1_handle, q[0]+math.pi/2, vrep.simx_opmode_oneshot )
        vrep.simxSetJointPosition(clientID,J2_handle, q[1], vrep.simx_opmode_oneshot )

        '''Enable streaming again (was automatically disabled with the positive event):'''
        err,buttonEventID,aux=vrep.simxGetUIEventButton(clientID,uiHandle,vrep.simx_opmode_streaming)

    time.sleep(0.01)

参考：

“逆运动学”——从操作空间到关节空间（上篇）