HDU 4890 One to Four（2014 Multi-University Training Contest 3）

题意：给定一个长方形网格，要把它切成完全相同4个部分（这里完全相同指可以旋转平移后能重叠）。把4个重叠后每个网格对应有四个数字相加，得到一种方案，所有格子中和最小就是该种方案的值，在多种方案中，最后问最大的解能使多少。

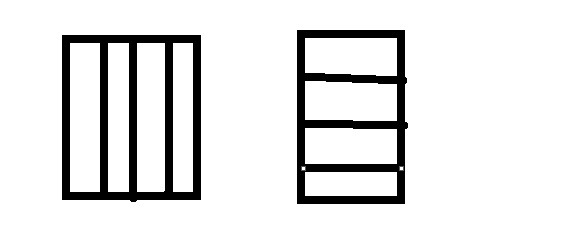
思路：首先任意一种划分可以映射到4个相同的长方形，也就是说一种不是长方形的方案可以转化为一种长方形的。那么我们就只需要找4个完全相同的长方形就可以。一共有以下画法：

下面画图时基于n>m。边长要满足一定条件要自己注意。

#include <iostream>

#include<cstdio>

#include<cstring>

#include<algorithm>

#include<cmath>

#define debug(x) printf(#x"= %d\n",x);

using namespace std;

struct node {

    int a[][];

    int n, m;

    void rota() {//旋转90度

        int b[][];

        for (int i = ; i < n; ++i) {

            for (int j = ; j < m; ++j) {

                b[j][n - i - ] = a[i][j];

            }

        }

        swap(n, m);

        for (int i = ; i < n; ++i)

            for (int j = ; j < m; ++j)

                a[i][j] = b[i][j];

    }

} p[], s;

int a[][];

int n, m;

int ans;

node cur[];

void gao(int now) {

    if (now == ) {

        for (int i = ; i < ; ++i)

            if (cur[i].n != cur[i + ].n || cur[i].m != cur[i + ].m)

                return;

        int minn = ;

        for (int i = ; i < cur[].n; ++i) {

            for (int j = ; j < cur[].m; ++j) {

                int sum = ;

                for (int k = ; k < ; ++k) {

                    sum += cur[k].a[i][j];

                }

                //    printf("%d %d %d\n",i,j,sum);

                if (sum < minn)

                    minn = sum;

            }

        }

        if (minn > ans)

            ans = minn;

        return;

    }

    cur[now] = p[now];

    gao(now + );

    for (int i = ; i < ; ++i) {

        cur[now].rota();

        gao(now + );

    }

}

int main() {

    while (scanf("%d%d", &n, &m) != EOF) {

        for (int i = ; i < n; ++i)

            for (int j = ; j < m; ++j)

                scanf("%d", &a[i][j]);

        //debug(m);

        ans = ;

        if (n %  == ) {

            for (int i = ; i < ; ++i) {

                for (int j = n /  * i; j < n /  * (i + ); ++j) {

                    for (int k = ; k < m; ++k) {

                        p[i].a[j % (n / )][k] = a[j][k];

                    }

                }

                p[i].n = n / ;

                p[i].m = m;

            }

            gao();

        }

        if (m %  == ) {

            for (int i = ; i < ; ++i) {

                for (int j = ; j < n; ++j) {

                    for (int k = i * (m / ); k < (i + ) * m / ; ++k) {

                        p[i].a[j][k % (m / )] = a[j][k];

                    }

                }

                p[i].n = n;

                p[i].m = m / ;

            }

            gao();

        }

        if (n %  ==  && m %  == ) {

            for (int i = ; i < ; ++i) {

                for (int j = (i / ) * n / ; j < (i /  + ) * n / ; ++j) {

                    for (int k = (i % ) * m / ; k < (i %  + ) * m / ;

                            ++k) {

                        p[i].a[j % (n / )][k % (m / )] = a[j][k];

                    }

                }

                p[i].n = n / ;

                p[i].m = m / ;

            }

            gao();

        }

        s.n = n;

        s.m = m;

        for (int i = ; i < n; ++i)

            for (int j = ; j < m; ++j)

                s.a[i][j] = a[i][j];

        if (n < m) {

            s.rota();

            swap(n, m);

        }

        if ( * s.n ==  * s.m && s.m %  ==  && s.n %  == ) {

            for (int i = ; i < ; ++i) {

                for (int j = ; j < m; ++j) {

                    for (int k = i * m / ; k < (i + ) * m / ; ++k) {

                        p[i].a[j][k % (m / )] = s.a[j][k];

                    }

                }

                p[i].n = m;

                p[i].m = m / ;

            }

            for (int i = m; i < n; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i - m][j] = s.a[i][j];

            p[].n = n - m;

            p[].m = m;

            gao();

            for (int i = ; i < ; ++i) {

                for (int j = n - m; j < n; ++j) {

                    for (int k = i * m / ; k < (i + ) * m / ; ++k) {

                        p[i].a[j - (n - m)][k % (m / )] = s.a[j][k];

                    }

                }

                p[i].n = m;

                p[i].m = m / ;

            }

            for (int i = ; i < n - m; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i][j] = s.a[i][j];

            p[].n = n - m;

            p[].m = m;

            gao();

        }

        if (s.n ==  * s.m && s.m %  == ) {

            for (int i = ; i < n / ; ++i)

                for (int j = ; j < m / ; ++j)

                    p[].a[i][j] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m / ;

            for (int i = ; i < n / ; ++i)

                for (int j = m / ; j < m; ++j)

                    p[].a[i][j - m / ] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m / ;

            for (int i = n / ; i < n /  * ; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i - n / ][j] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m;

            for (int i = n /  * ; i < n; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i - n /  * ][j] = s.a[i][j];

            p[].n = n / ;

            p[].m = m;

            gao();

            for (int i = n / ; i < n /  * ; ++i)

                for (int j = ; j < m / ; ++j)

                    p[].a[i - n / ][j] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m / ;

            for (int i = n / ; i < n /  * ; ++i)

                for (int j = m / ; j < m; ++j)

                    p[].a[i - n / ][j - m / ] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m / ;

            for (int i = ; i < n / ; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i][j] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m;

            for (int i = n /  * ; i < n; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i - n /  * ][j] = s.a[i][j];

            p[].n = n / ;

            p[].m = m;

            gao();

            for (int i = n / ; i < n; ++i)

                for (int j = ; j < m / ; ++j)

                    p[].a[i - n / ][j] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m / ;

            for (int i = n / ; i < n; ++i)

                for (int j = m / ; j < m; ++j)

                    p[].a[i - n / ][j - m / ] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m / ;

            for (int i = ; i < n / ; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i][j] = s.a[i][j];

            p[].n = s.n / ;

            p[].m = s.m;

            for (int i = n / ; i < n / ; ++i)

                for (int j = ; j < m; ++j)

                    p[].a[i - n / ][j] = s.a[i][j];

            p[].n = n / ;

            p[].m = m;

            gao();

        }

        printf("%d\n", ans);

    }

    return ;

}

HDU 4890 One to Four（2014 Multi-University Training Contest 3）的更多相关文章

hdu 5003 模拟水题（2014鞍山网赛G题）
你的一系列得分先降序排列再按0.95^(i-1)*ai 这个公式计算你的每一个得分最后求和 Sample Input12530 478Sample Output984.1000000000 # ...
千寻浏览器 1.0 Beta 1(524)（2014年5月27日）
千寻浏览器--又一款新生浏览器今天进入各位浏览迷的视野.千寻浏览器基于IE内核,据传是由百度浏览器的上海团队操刀,在功能定位上,与目前的QQ浏览器有些相似. 千寻来自官方的解释:寻,追寻,探索,又是古 ...
HDU 3416 Marriage Match IV （最短路径，网络流，最大流）
HDU 3416 Marriage Match IV (最短路径,网络流,最大流) Description Do not sincere non-interference. Like that sho ...
（ 2018 Multi-University Training Contest 2）
2018 Multi-University Training Contest 2) HDU 6311 Cover HDU 6312 Game HDU 6313 Hack It HDU 6314 Mat ...
HDU 4897 Little Devil I（树链剖分）（2014 Multi-University Training Contest 4）
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4897 Problem Description There is an old country and ...
HDU 4906 Our happy ending（2014 Multi-University Training Contest 4）
题意:构造出n个数这n个数取值范围0-L,这n个数中存在取一些数之和等于k,则这样称为一种方法.给定n,k,L,求方案数. 思路:装压每位第1为表示这种方案能不能构成1(1表示能0表示不能) ...
hdu 5475 An easy problem（暴力 || 线段树区间单点更新）
http://acm.hdu.edu.cn/showproblem.php?pid=5475 An easy problem Time Limit: 8000/5000 MS (Java/Others ...
HDU - 3966 Aragorn's Story（树链剖分入门+线段树）
HDU - 3966 Aragorn's Story Time Limit: 3000MS Memory Limit: 32768KB 64bit IO Format: %I64d & ...
UVALive 7141 BombX（离散化+线段树）（2014 Asia Shanghai Regional Contest）
题目链接:https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=6 ...

随机推荐

Java中的数学运算BigDecimal
Math类 package ch7; /** * Created by Jiqing on 2016/11/24. */ public class MathDemo { public static v ...
在Spark上用Scala实验梯度下降算法
首先参考的是这篇文章:http://blog.csdn.net/sadfasdgaaaasdfa/article/details/45970185 但是其中的函数太老了.所以要改.另外出发点是我自己的 ...
html的空格和换行显示【摘自网络】
一.HTML 代码中的所有连续的空格或空行(换行)都会被显示为一个空格,不管是内容还是标签之间. 二.当我们想让它们在同一行连续显示时,就让所有的代码之间没有空格,也不要换行. 三.当我们想要显示连续 ...
javascript 键盘事件总结
原文:http://www.cnblogs.com/rubylouvre/archive/2009/08/20/1550526.html#2583814 在进入正题前,我们看一下浏览器对于键盘的一些默 ...
J2EE 第二阶段项目之分析业务
这次的项目为: 两金申报系统.主要是关系的练习,CRUD,统计. 这个项目没有pdf图,只有一本使用手册.(在我们出去工作后,做项目的时候,也可能只有项目需求的资料). 分析:每一张表都有分页,查看 ...
为什么要baidu/Google问题尽量少在群里问问题
群里问也是可以的但是不能指望群里的人详细的回答有时候的回答会很到位但是也可以应该更多的去网络上搜索信息因为那是别人已经写好的我们为什么不顺便去获取呢别人花费了精力我们要尽量运用 ...
如何使用 declare-styleable
如何使用 declare-styleable 在创建 xml 到 objectName/res/values/ 命名为 attrs.xml 编辑文件内容为(示例)<?xml version=&q ...
Google V8扩展利器发布：v8-native-binding-generator
用C++扩展Google V8很简单,但是类比较多时还是很烦的.前段时间开发cantk-runtime-v8时,我写了一个代码产生器v8-native-binding-generator,让扩展Goo ...
常用SQL语句（交互）
%-------通配符 select * from [EMoney_Club].[dbo].[GoldIdea_AdviceCollect] where [Content] like '%昵称%' s ...
linux笔记：用户管理命令和用户组管理命令
用户管理命令命令名称:useradd功能:添加用户(添加完后不能立即使用,必须用passwd修改用户密码后才能使用)用法:useradd [选项] 用户名选项参数:-u 手工指定用户的UID-d 手 ...

HDU 4890 One to Four（2014 Multi-University Training Contest 3）

HDU 4890 One to Four（2014 Multi-University Training Contest 3）的更多相关文章

随机推荐

热门专题