P5309 [Ynoi2011] 初始化 题解

题目链接：初始化

这种 ynoi 的老题就是卡常。来简单说说这题的思维切入口。

看到形如 \(y+k \times x\) 的结构，自然而然思考一下如果我们是暴力更新会有怎么样的效果。我们容易发现，如果 \(x\) 比较大，暴力更新的次数 \(\dfrac{n}{x}\) 也不会很大的，但 \(x\) 如果很小，那么就会更新次数很大了。这启发我们按 \(x\) 的大与小两种情况进行各自地优化处理。那么这个思想其实就是“根号分治思想”：

1. 对 \(x > \sqrt{n}\) 的修改，进行暴力更新，同时维护块区间之和，这里复杂度为 \(\sqrt{n}\)。

2. 对 \(x \le \sqrt{n}\) 的修改，我们另寻途径，优化它的复杂度。

怎么解决小步长呢，我们容易发现如果每次都是 \(+x\) 以后的位置进行修改，如果我们的块长 等于 \(x\) 就好了。这样一来，对于块长为 \(x\) 的区间，你会发现每个区间同样的相对位置发生修改了。

我们可以发现每个块的变化都是一致的，都是同一个块同一个位置发生单点变化，同时我们又注意到此时此刻不同长度的 \(x\) 显然数量不超过 \(\sqrt{n}\)，这启发我们为每一种不同块长维护一个代表块的信息。

我们抽象地拿出一块作为代表块，观察它的信息。

对于每个不同长度的块，为了知道在查询时它们对应的块和，但同时注意到每个整块对应的样子都是一样的，这启发我们可以维护块内前缀和，而拿到每个块内之和。当然我们注意到分块的查询的特点：偶尔会有散块查询。

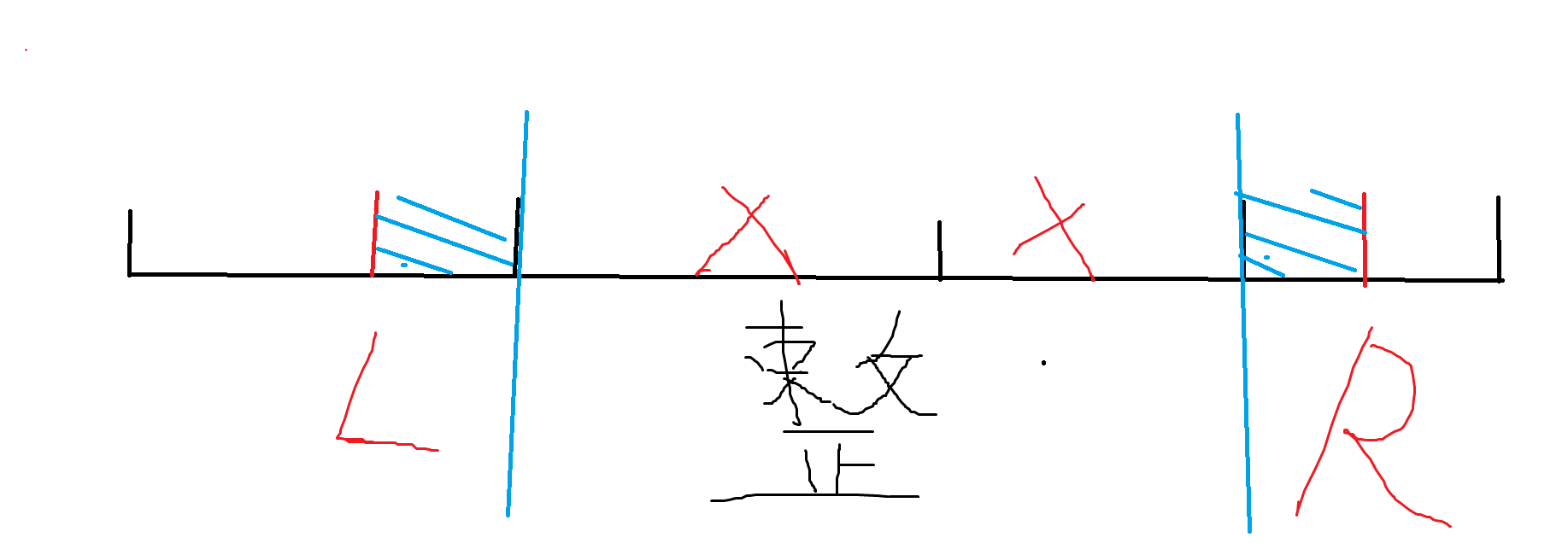
容易发现散块，我们可以用前缀和作差算出来，但由于涉及到需要计算当前块的左右端点下标，我们为了方便的书写，可以同时维护块后缀和，使得代码层面上更易理解，即 \(L\) 到它对应的块右端点之和显然为 \(suf_L\) 后缀和。这样一来，我们就能知道步长为 \(x\) 的每个整块内的情况了。同时我们注意到 \(y<=x\) ，所以 起点一定是在第一个块的，每个块情况是一模一样的。

卡常细节

首先由于具有取模操作，所以我们可以考虑用先全部加起来，最后再取模。另外注意到每次遍历不同块长的 \(x\) 的前后缀和情况，有些 \(x\) 可能并未出现过，所以我们可以记录下出现过的块长在哈希表中用于遍历使用。最后可以考虑上快读之类的东西。对于原数组如果未发生大块修改，可以直接前缀和求区间和。

参照代码

#include <bits/stdc++.h>

//#pragma GCC optimize("Ofast,unroll-loops")

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 2e5 + 10;
constexpr int MOD = 1e9 + 7;
constexpr int Size = sqrt(N) + 1;
constexpr int Cnt = (N + Size - 1) / Size + 1;
#define pointPos(t,x) ((t-1)%x+1) //求出某个位置在指定块长中应该对应的块内编号
#define blockId(t,x) ((t-1)/x+1) //求出某个位置在指定块长对应块编号
unordered_set<int> vis; //出现过的块长
int cnt, siz;
int pre[Size][Size], suf[Size][Size];//不同块长内部的前后缀和
int a[N];
int n, q;
int s[N], e[N];//块的起点和
int sum[Cnt]; //块和
int OldPre[N];//原数组的前缀和
bool isBigUpdate;

inline void BigUpdate(const int x, int y, const int z)
{
    for (; y <= n; y += x)
    {
        const int id = blockId(y, siz);
        a[y] = (a[y] + z) % MOD, sum[id] = (sum[id] + z) % MOD;
    }
}

inline void SmallUpdate(const int x, const int y, const int z)
{
    forn(i, 1, y)suf[x][i] = (suf[x][i] + z) % MOD;
    forn(i, y, x)pre[x][i] = (pre[x][i] + z) % MOD;
}

inline int OldQuery(const int l, const int r)
{
    const int L = blockId(l, siz), R = blockId(r, siz);
    ll ans = 0;
    if (L == R)
    {
        forn(i, l, r)ans += a[i];
        return ans % MOD;
    }
    forn(i, l, e[L])ans += a[i];
    forn(i, s[R], r)ans += a[i];
    forn(i, L+1, R-1)ans += sum[i];
    return ans % MOD;
}

inline int Query(const int l, const int r)
{
    ll ans = isBigUpdate ? OldQuery(l, r) : OldPre[r] - OldPre[l - 1];
    //遍历每一种块长
    for (auto x : vis)
    {
        const int L = blockId(l, x), R = blockId(r, x);
        const int Lpos = pointPos(l, x), Rpos = pointPos(r, x);
        if (L == R)ans += pre[x][Rpos] - pre[x][Lpos - 1];
        else ans += ll(R - L - 1) * pre[x][x] + suf[x][Lpos] + pre[x][Rpos];
    }
    return modt(ans, MOD);
}

inline void solve()
{
    read(n, q);
    siz = sqrt(n);
    cnt = (n + siz - 1) / siz;
    forn(i, 1, n)read(a[i]), OldPre[i] = (OldPre[i - 1] + a[i]) % MOD;
    forn(i, 1, cnt)s[i] = (i - 1) * siz + 1, e[i] = i * siz;
    e[cnt] = n;
    forn(i, 1, cnt)forn(j, s[i], e[i])sum[i] = (sum[i] + a[j]) % MOD;
    forn(i, 1, q)
    {
        int op;
        read(op);
        if (op == 1)
        {
            int x, y, z;
            read(x, y, z);
            if (x > siz)BigUpdate(x, y, z), isBigUpdate = true;
            else SmallUpdate(x, y, z), vis.insert(x);
        }
        else
        {
            int l, r;
            read(l, r);
            write(endl, Query(l, r));
        }
    }
}

signed int main()
{
    Spider
    //------------------------------------------------------
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
}

\[ 最终时间理论最坏复杂度为\ O((n+q)\sqrt{n})
\]