Mahout系列之----距离度量
x = (x1,...,xn) 和y = (y1,...,yn) 之间的距离为
(1)欧氏距离 EuclideanDistanceMeasure

(2)曼哈顿距离 ManhattanDistanceMeasure
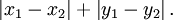
(3)马氏距离MahalanobisDistanceMeasure
马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。 对于一个均值为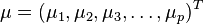 ,协方差矩阵为
,协方差矩阵为 的多变量向量
的多变量向量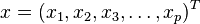 ,其马氏距离为
,其马氏距离为
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为 的随机变量
的随机变量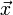 与
与 的差异程度:
的差异程度:
如果协方差矩阵为单位矩阵,马氏距离就简化为欧氏距离;如果协方差矩阵为对角阵,其也可称为正规化的欧氏距离。
其中 是
是 的标准差。
的标准差。
(4)余弦距离 CosineDistanceMeasure
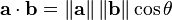
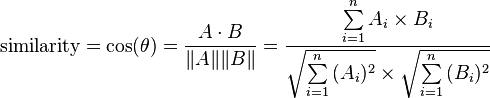
(5)汉明距离
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。 例如:
10101 与10101 之间的汉明距离是 2。
2396 与2396 之间的汉明距离是 3。
"toned" 与 "roses" 之间的汉明距离是 3。
(6)平方欧几里德距离度量 SquaredEuclideanDistanceMeasure

(7)Tanimoto距离 TanimotoDistanceMeasure

(8)加权距离度量 WeightedDistanceMeasure ,具体实现有:WeightedEuclideanDistanceMeasure和WeightedManhattanDistanceMeasure
用欧几里德距离和曼哈顿距离实现。加权距离度量是Mahout的高级特征,它能让你在不同维上赋予不同的权重,以此对距离度量信息产生影响,WeightedDistanceMeasure在向量格式化中需要序列化为文件。变量对距离的影响是不一样的,通过权值来确定。
(9)切比雪夫距离 ChebyshevDistanceMeasure

Mahout系列之----距离度量的更多相关文章
- Mahout 系列之--canopy 算法
Canopy 算法,流程简单,容易实现,一下是算法 (1)设样本集合为S,确定两个阈值t1和t2,且t1>t2. (2)任取一个样本点p属于S,作为一个Canopy,记为C,从S中移除p. (3 ...
- <转>从K近邻算法、距离度量谈到KD树、SIFT+BBF算法
转自 http://blog.csdn.net/likika2012/article/details/39619687 前两日,在微博上说:“到今天为止,我至少亏欠了3篇文章待写:1.KD树:2.神经 ...
- 从K近邻算法、距离度量谈到KD树、SIFT+BBF算法
转载自:http://blog.csdn.net/v_july_v/article/details/8203674/ 从K近邻算法.距离度量谈到KD树.SIFT+BBF算法 前言 前两日,在微博上说: ...
- ML 07、机器学习中的距离度量
机器学习算法 原理.实现与实践 —— 距离的度量 声明:本篇文章内容大部分转载于July于CSDN的文章:从K近邻算法.距离度量谈到KD树.SIFT+BBF算法,对内容格式与公式进行了重新整理.同时, ...
- 海量数据挖掘MMDS week2: LSH的距离度量方法
http://blog.csdn.net/pipisorry/article/details/48882167 海量数据挖掘Mining Massive Datasets(MMDs) -Jure Le ...
- 距离度量以及python实现(一)
1. 欧氏距离(Euclidean Distance) 欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式. (1)二维平面上两点a(x1,y1)与b(x2,y2)间 ...
- 概率分布之间的距离度量以及python实现(三)
概率分布之间的距离,顾名思义,度量两组样本分布之间的距离 . 1.卡方检验 统计学上的χ2统计量,由于它最初是由英国统计学家Karl Pearson在1900年首次提出的,因此也称之为Pearson ...
- 机器学习方法、距离度量、K_Means
特征向量 1.特征向量:以人为例,每个元素可能就对应这人的某些方面,这就是特征,例如:身高.年龄.性别.国际....2.特征工程:目的就是将现有数据中可作为信号的特征与那些仅是噪声的特征区分开来:当数 ...
- 概率分布之间的距离度量以及python实现
1. 欧氏距离(Euclidean Distance) 欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式.(1)二维平面上两点a(x1,y1)与b(x2,y2)间的欧 ...
随机推荐
- Android中软键盘弹出时底部菜单上移问题
当在Android的layout设计里面如果输入框过多,则在输入弹出软键盘的时候,下面的输入框会有一部分被软件盘挡住,从而不能获取焦点输入. 解决办法: 方法一:在你的activity中的oncrea ...
- Android等宽字体
Android等宽字体 效果图 在xml中设置 添加属性 android:typeface="monospace" 例如 <TextView android:layout_w ...
- iOS学习笔记--数据存储
iOS应用数据存储的常用方式 XML属性列表(plist)归档 Preference(偏好设置) NSKeyedArchiver归档(NSCoding) SQLite3 Core Data 1. XM ...
- 阿里云手动安装特定版本的nginx
想添加nginx的缓存功能, 结果1.4.6还不支持. apt-get remove nginx 374 sudo apt-key add nginx_signing.key 375 deb http ...
- 在 Mac OS X 10.10 安装 pyenv 的一个小坑
小记一下. 因为全面转向 Python 3.4 作为主力开发版本,但是手上的 Mac OS X 和服务器上用的都是 Python 2.7,所以需要安装 pyenv. 按其 github 页面的说明,使 ...
- Android实现自动更新功能
Android实现自动更新功能 Android自动更新的功能可以使用第三方的SDK来实现,但是类似友盟,就不支持x86手机的自动更新,科大讯飞,弹窗是全局的,小米手机就会默认把弹窗权限关掉不允许弹出提 ...
- Latex居中
居中文本 环境:\begin{center} 第一行\\第二行\\...第n行 \end{center}.可以用\\[长度]来插入可以省略的额外行间距.在一个环境内部,可以用命令\centering来 ...
- ToolBar与AppcompatAcitivity实现浸入式Statusbar效果
toolbar是android sdk API21新增的组件,下面是谷歌官方的介绍文档: A standard toolbar for use within application content. ...
- 剑指Offer——网易笔试之解救小易——曼哈顿距离的典型应用
剑指Offer--网易笔试之解救小易--曼哈顿距离的典型应用 前言 首先介绍一下曼哈顿,曼哈顿是一个极为繁华的街区,高楼林立,街道纵横,从A地点到达B地点没有直线路径,必须绕道,而且至少要经C地点,走 ...
- 网页搜索之后的APP搜索
搜索技术是互联网最核心的技术之一.但是移动互联网迅猛发展的今天,互联网产生的数据已经不是简单的网页搜索所能涵盖的了.比如微信公众号,产生了许多优质的内容,如果这些公众号仅仅将这些内容发布到微信平台,那 ...



