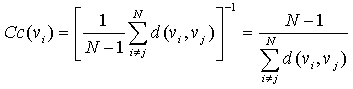PTA 社交网络图中结点的“重要性”计算(30 分)
7-12 社交网络图中结点的“重要性”计算(30 分)
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi的“紧密度中心性”Cc(vi)数学上定义为vi到其余所有结点vj (j≠i) 的最短距离d(vi,vj)的平均值的倒数:
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(≤104)是图中结点个数,顺便假设结点从1到N编号;M(≤105)是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤100)以及K个结点编号,用空格分隔。
输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35
PTA 的数据之水我都没想到,可以说是非常之水了,floyd都能过了:
#include<bits/stdc++.h>
using namespace std;
#define inf 99999999
int n,m;
const int maxn = 10010;
int maps[maxn][maxn];
int qus[maxn];
double ans[maxn];
void floyd()
{
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
if(maps[i][k]<inf && maps[k][j]<inf && maps[i][j]>maps[i][k]+maps[k][j])
maps[i][j]=maps[i][k]+maps[k][j];
}
int calcu(int x)
{
int ans = 0;
for(int i=1;i<=n;i++)
{
if(x!=i) ans += maps[x][i];
}
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
maps[i][j] = inf;
int a,b,k;
while(m--){
cin>>a>>b;
maps[a][b] = 1;
maps[b][a] = 1;
}
floyd();
/*for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
printf("%d%c",maps[i][j],j==n?'\n':' ');
*/
cin>>k;
for(int i=1;i<=k;i++)
cin>>qus[i];
for(int i=1;i<=k;i++)
{
//printf("%d\n",calcu(qus[i]));
printf("Cc(%d)=%.2lf\n",qus[i],(n-1)*1.0/(calcu(qus[i]*1.0)));
}
}
PTA 社交网络图中结点的“重要性”计算(30 分)的更多相关文章
- PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分)
PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分) 7-36 社交网络图中结点的“重要性”计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某 ...
- 社交网络图中结点的“重要性”计算 (30 分) C++解法
社交网络图中结点的"重要性"计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓 ...
- PTA 7-12(图) 社交网络图中结点的“重要性”计算 最短路
7-12(图) 社交网络图中结点的“重要性”计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的 ...
- 7-10 社交网络图中结点的“重要性”计算(30 point(s)) 【并查集+BFS】
7-10 社交网络图中结点的"重要性"计算(30 point(s)) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络 ...
- 7-11 社交网络图中结点的“重要性”计算 (30 分)(Dijkstra算法)
题意: 思路:对每个输入的点跑一遍dijkstra算法,然后对这个点到所有点的距离求和按公式输出就可以了. (这次尝试了用数组模拟链表来做最短路问题,刷新了自己对最短路的理解) 这里构造链表的过程我 ...
- PTA 7-2 二叉搜索树的结构(30 分)
7-2 二叉搜索树的结构(30 分) 二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值:若它的右子树不空,则右子树上所有结点的值均大 ...
- PTA 7-2 是否完全二叉搜索树(30 分) 二叉树
将一系列给定数字顺序插入一个初始为空的二叉搜索树(定义为左子树键值大,右子树键值小),你需要判断最后的树是否一棵完全二叉树,并且给出其层序遍历的结果. 输入格式: 输入第一行给出一个不超过20的正整数 ...
- Excel中最精确的计算年龄的公式
身份证算年龄 假设A1是身份证号所在单元格 =IF(MONTH(NOW())<INT(MID(A1,11,2)),INT(YEAR(NOW())-INT(MID(A1,7,4)))-1,IF(M ...
- dgraph解决社交关系中的正反向查找
dgraph解决社交关系中的正反向查找 本篇介绍的是, 社交关系中的关注者与被关注者在dgraph中如何实现查找. 对dgraph的基本操作不太清楚的可以看看我之前写的博客 dgraph实现基本操作 ...
随机推荐
- 通过java api统计hive库下的所有表的文件个数、文件大小
更新hadoop fs 命令实现: [ss@db csv]$ hadoop fs -count /my_rc/my_hive_db/* 18/01/14 15:40:19 INFO hdfs.Peer ...
- background属性的学习整理转述
前言:这是笔者学习之后自己的理解与整理.如果有错误或者疑问的地方,请大家指正,我会持续更新! background我们一般用到的的属性有: background-attachment:背景(图片)是否 ...
- if else if,switch case二者的联系与区别
前段时间在学习中听到了一个关于条件判断语句的问题,分析if else if语句和switch case语句这两者之间的联系和区别,从而使用其中最有效率的一种方法. 一.if...else if if. ...
- C#在使用Assembly加载程序集时失败
错误现象: 进行插件读取时出现错误:"尝试从一个网络位置加载程序集,在早期版本的 .NET Framework 中,这会导致对该程序集进行沙盒处理.此发行版的 .NET Framework ...
- Java 异常基础详解
目录 1. Java 中的异常 1.1 什么是异常? 1.2 什么是异常处理? 1.2.1 异常处理的优势 1.3 Java 异常类的层次结构 1.4 异常类型 1.5 检查和未检查异常之间的区别 1 ...
- Django REST framework+Vue 打造生鲜超市(十一)
十二.支付宝沙箱环境配置 12.1.创建应用 进入蚂蚁金服开放平台(https://open.alipay.com/platform/home.htm),登录后进入管理中心-->>应用列表 ...
- [LeetCode] Diameter of Binary Tree 二叉树的直径
Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a b ...
- CentOS搭建Apache+php+MySQL+Redis环境
要搭建一个本地linux服务器环境,按照网络教程依葫芦画瓢,噼里啪啦搭好后,发现redis服务怎么也弄不好,不喜欢那种明知有问题却无从下手又无能为力的感觉,碰了无数次壁以后,我决定卸载,重头来过,并尽 ...
- pdf如何转换为word文档
我们经常会遇到需要将PDF转换为WORD文档,对于我来讲,有些PDF没有目录,看起来非常不方便,于是就特别想转成WORD,然后增加目录,想看某一节内容时,快速查找. 这里我总结了一些方法,后续也会不断 ...
- 实验吧_程序逻辑问题(代码审计)&上传绕过
一开始我先随便输入了几个账号名字进行测试,发现当输入的账号名为admin时会发生报错 经过测试果然是一个注入点 当拿到admin密码后发现根本没用,没办法另寻他路 审查元素时发现提示index.txt ...