贝叶斯、朴素贝叶斯及调用spark官网 mllib NavieBayes示例
贝叶斯定理便是基于下述贝叶斯公式:
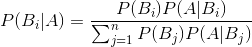
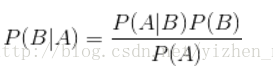
P(B|A)随着P(B)和P(A|B)的增长而增长,随着P(A)的增长而减少,即如果A独立于B时被观察到的可能性越大,那么A对B的支持度越小
朴素贝叶斯
朴素贝叶斯算法是假设各个特征之间相互独立,使用贝叶斯公式进行分类的。请参考:https://blog.csdn.net/amds123/article/details/70173402
spark NavieBayes 官方示例代码如下:
import org.apache.spark.ml.classification.NaiveBayes
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
import org.apache.spark.sql.SparkSession object NavieBayesDemo {
def main(args: Array[String]): Unit = {
val spark = SparkSession
.builder
.appName("NavieBayesDemo").master("local")
.config("spark.sql.warehouse.dir", "C:\\study\\sparktest")
.getOrCreate()
// Load the data stored in LIBSVM format as a DataFrame.
val dataset=spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")
// Split the data into training and test sets (30% held out for testing)
val Array(tranningData,testData)=dataset.randomSplit(Array(0.7,0.3),seed = 1234L) // Train a NavieBayes model
val model = new NaiveBayes().fit(tranningData)
// Select example rows to display.
val predictions=model.transform(testData)
predictions.show() // Select (prediction, true label) and compute test error
val evaluator = new MulticlassClassificationEvaluator()
.setLabelCol("label")
.setPredictionCol("prediction")
.setMetricName("accuracy")
val accuracy = evaluator.evaluate(predictions)
println(s"Test set accuracy = $accuracy") spark.stop()
}
}
运行结果如下:
Test set accuracy = 1.0
贝叶斯、朴素贝叶斯及调用spark官网 mllib NavieBayes示例的更多相关文章
- 模式识别之贝叶斯---朴素贝叶斯(naive bayes)算法及实现
处女文献给我最喜欢的算法了 ⊙▽⊙ ---------------------------------------------------我是机智的分割线----------------------- ...
- Spark官网资料学习网址
百度搜索Spark: 这一个是Spark的官网网址,你可以在上面下载相关的安装包等等. 这一个是最新的Spark的文档说明,你可以查看如何安装,如何编程,以及含有对应的学习资料.
- Spark官网
Components Spark applications run as independent sets of processes on a cluster, coordinated by the ...
- Spark 官网提到的几点调优
1. 数据序列化 默认使用的是Java自带的序列化机制.优点是可以处理所有实现了java.io.Serializable 的类.但是Java 序列化比较慢. 可以使用Kryo序列化机制,通常比Java ...
- Logistic 最大熵 朴素贝叶斯 HMM MEMM CRF 几个模型的总结
朴素贝叶斯(NB) , 最大熵(MaxEnt) (逻辑回归, LR), 因马尔科夫模型(HMM), 最大熵马尔科夫模型(MEMM), 条件随机场(CRF) 这几个模型之间有千丝万缕的联系,本文首先会 ...
- 【机器学习实战】第4章 朴素贝叶斯(Naive Bayes)
第4章 基于概率论的分类方法:朴素贝叶斯 朴素贝叶斯 概述 贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类.本章首先介绍贝叶斯分类算法的基础——贝叶斯定理.最后,我们 ...
- 【sklearn朴素贝叶斯算法】高斯分布/多项式/伯努利贝叶斯算法以及代码实例
朴素贝叶斯 朴素贝叶斯方法是一组基于贝叶斯定理的监督学习算法,其"朴素"假设是:给定类别变量的每一对特征之间条件独立.贝叶斯定理描述了如下关系: 给定类别变量\(y\)以及属性值向 ...
- 调用spark API,监控任务的进度
我们现在需要监控datapre0这个任务每一次执行的进度,操作如下: 1. 如图所示,打开spark管理页面,找到对应的任务,点击任务名datapre0 2. 进去之后,获得对应IP和端口 3. 访 ...
- 朴素贝叶斯算法源码分析及代码实战【python sklearn/spark ML】
一.简介 贝叶斯定理是关于随机事件A和事件B的条件概率的一个定理.通常在事件A发生的前提下事件B发生的概率,与在事件B发生的前提下事件A发生的概率是不一致的.然而,这两者之间有确定的关系,贝叶斯定理就 ...
随机推荐
- 信号量及P/V操作
有一个厕所,允许多个男生同时使用,也允许一个女生使用,但是不允许男女共用(那岂不是乱了套)通过厕所门口有一个三面小牌子来运行.一面是男生在用,第二面是女生在用,第三面是空.运行机制:第一个进入空厕所男 ...
- Visual C++ 6.0中if语句的常见问题
# include <stdio.h> int main (void) { > )//如果在第四行加分号的话,编译的时候就会在第六行出错 printf("你好\n" ...
- 列表中使用嵌套for循环[i*j for i in range(3) for j in range(3)]
利用嵌套for循环形成一个新列表 [i*j for i in range(3) for j in range(3)]相当于如下代码 li=[] for i in range(3): for j in ...
- jmeter使用手册
1.在bin文件中找到jmeter.bat文件启动 2.创建测试计划-填写计划名称 3.添加线程组(右键点击) 4.设置线程-红框内均可设置,线程数-并发次数 5.在线程组下添加http请求 6.在h ...
- asp.net实现伪静态
一.配置应用程序 1.下载URLRewrite.dll,程序中添加引用 2.在web.config中配置 <configuration> <configSections> &l ...
- word2007无法打开.doc
如果您的WORD2007无法打开.DOC文档,可以试试如下的方法 打开注册表编辑器(开始-运行-输入regedit VISTA中在开始菜单最下方的搜索栏内输入regedit) 展开HKEY_CLASS ...
- PTA3
一.7-1 抓老鼠啊~亏了还是赚了? (20 分) 某地老鼠成灾,现悬赏抓老鼠,每抓到一只奖励10元,于是开始跟老鼠斗智斗勇:每天在墙角可选择以下三个操作:放置一个带有一块奶酪的捕鼠夹(T),或者放置 ...
- web爬虫,BeautifulSoup
BeautifulSoup 该模块用于接收一个HTML或XML字符串,然后将其进行格式化,之后遍可以使用他提供的方法进行快速查找指定元素,从而使得在HTML或XML中查找指定元素变得简单. 1 2 3 ...
- RabbitMQ全网资料收集
RabbitMQ是一个由erlang开发的AMQP(Advanced Message Queue )的开源实现.AMQP 的出现其实也是应了广大人民群众的需求,虽然在同步消息通讯的世界里有很多公开标准 ...
- Go实例解析
Go语言包的加载顺序如图 可以通过如下实例详细了解 代码来源于<Go实战> 代码地址:https://github.com/goinaction/code 项目代码结构 程序架构 首先分析 ...
