opencv源码学习: getGaussianKernel( 高斯核）；

参考： https://blog.csdn.net/u012633319/article/details/80921023

二维高斯核， 可以根据下面的公式推到为两个一维高斯核的乘积：

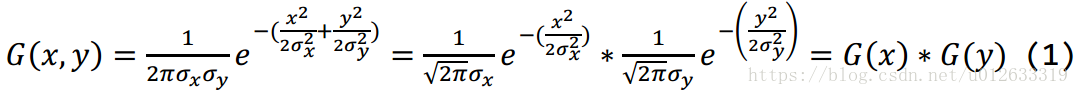
原型：

/** @brief Returns Gaussian filter coefficients.

The function computes and returns the \f$\texttt{ksize} \times 1\f$ matrix of Gaussian filter
coefficients:

\f[G_i= \alpha *e^{-(i-( \texttt{ksize} -1)/2)^2/(2* \texttt{sigma}^2)},\f]

where \f$i=0..\texttt{ksize}-1\f$ and \f$\alpha\f$ is the scale factor chosen so that \f$\sum_i G_i=1\f$.

Two of such generated kernels can be passed to sepFilter2D. Those functions automatically recognize
smoothing kernels (a symmetrical kernel with sum of weights equal to 1) and handle them accordingly.
You may also use the higher-level GaussianBlur.
@param ksize Aperture size. It should be odd ( \f$\texttt{ksize} \mod 2 = 1\f$ ) and positive.
@param sigma Gaussian standard deviation. If it is non-positive, it is computed from ksize as
`sigma = 0.3*((ksize-1)*0.5 - 1) + 0.8`.
@param ktype Type of filter coefficients. It can be CV_32F or CV_64F .
@sa  sepFilter2D, getDerivKernels, getStructuringElement, GaussianBlur
 */
CV_EXPORTS_W Mat getGaussianKernel( int ksize, double sigma, int ktype = CV_64F );

源码分析:

cv::Mat cv::getGaussianKernel( int n, double sigma, int ktype )
{
    const int SMALL_GAUSSIAN_SIZE = ;
    static const float small_gaussian_tab[][SMALL_GAUSSIAN_SIZE] =
    {
        {.f},
        {0.25f, 0.5f, 0.25f},
        {0.0625f, 0.25f, 0.375f, 0.25f, 0.0625f},
        {0.03125f, 0.109375f, 0.21875f, 0.28125f, 0.21875f, 0.109375f, 0.03125f}
    };

    //判断是否满足预置的高斯模板；
    const float* fixed_kernel = n %  ==  && n <= SMALL_GAUSSIAN_SIZE && sigma <=  ?
        small_gaussian_tab[n>>] : ;

    CV_Assert( ktype == CV_32F || ktype == CV_64F );　　　　　　　　　　//仅支持两种格式，  32, 64位；
    Mat kernel(n, , ktype);　　　　　　　　　　　　　　　　　　//创建核模板， ktype为指定的类型；
    float* cf = kernel.ptr<float>();
    double* cd = kernel.ptr<double>();
    //如果sigma < 0, 那么更具模板尺寸计算sigma;
    double sigmaX = sigma >  ? sigma : ((n-)*0.5 - )*0.3 + 0.8;
    double scale2X = -0.5/(sigmaX*sigmaX);
    double sum = ;

    int i;
    for( i = ; i < n; i++ )
    {
        double x = i - (n-)*0.5;
        double t = fixed_kernel ? (double)fixed_kernel[i] : std::exp(scale2X*x*x);                //使用预置模板或者根据高斯函数计算高斯模板；
        if( ktype == CV_32F )　　　　　　　　　　//把计算得到的核填到模板中；
        {
            cf[i] = (float)t;
            sum += cf[i];
        }
        else
        {
            cd[i] = t;
            sum += cd[i];
        }
    }

    sum = ./sum;
    for( i = ; i < n; i++ )　　　　　　　　　　　　//归一化；
    {
        if( ktype == CV_32F )
            cf[i] = (float)(cf[i]*sum);
        else
            cd[i] *= sum;
    }

    return kernel;
}