D: Starry的神奇魔法（矩阵快速幂）

题目链接：https://oj.ismdeep.com/contest/Problem?id=1284&pid=3

D: Starry的神奇魔法

Time Limit: 1 s      Memory Limit: 128 MB     

Submit My Status

Problem Description

啦啦啦，Starry正愉快的做着编程题，代码是多么优美呀！突然，有人问他一道数学题，对于数学渣渣的Starry来说，这是多么的烦恼呀。不过不要紧，他还可以问其他人的，所以他想到了聪明的你们。这个问题是由一个神奇的魔法师提出的，他创造了一种魔法，每次使用魔法可以让今天的魔力值为前一天魔力值的2018倍+前两天魔力值的8倍+前三天魔力值的12倍。当然，一天只能使用一次魔法，除了使用魔法外，每天魔法师还能产生8888的魔力值。第一、二、三天的初始魔力值为888。他想问的是第n天他可以拥有多少魔力值。

Input

第一行输入一个T表示有TT个问题(1≤T≤104)(1≤T≤104)。

接下来T行，每行有一个数n（1≤n≤1018）n（1≤n≤1018），表示第nn天。

Output

输出TT行，每行输出第nn天的魔力值，由于数很大，结果对2018081220180812取模。

Sample Input

3
2
5
8

Sample Output

888
17299052
16854116

题目大意：f[1]=f[2]=f[3]=888;给出任意n（1<=n<=10^18),求f(n) = 2018*f(n-1)+8*f(n-2)+12*f(n-3)+8888。

解题思路：由递推公式我们可以得到以下矩阵：

通过递推可得到矩阵：

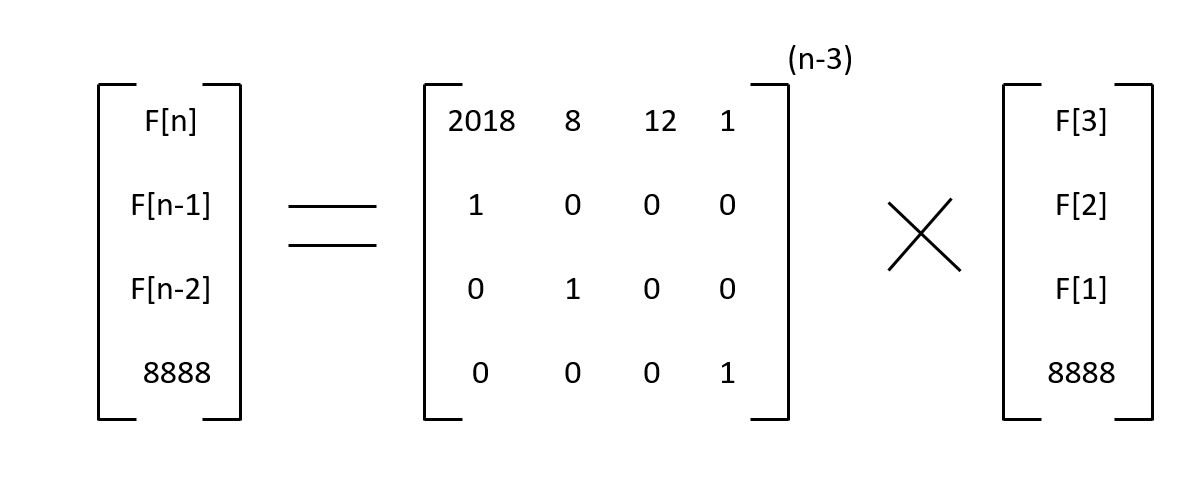
当n<=3时，直接输出888；

而当n>3时，直接计算上述矩阵式，先求出第一个矩阵的n-3次方，然后只要用第一个矩阵的第一行与第二个矩阵的第一列对应相乘相加即可得到答案。

附上代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;
const int mod=;
const int maxn=;
typedef long long ll;
struct Matrix{
    ll a[maxn][maxn];
};

Matrix mul(Matrix a,Matrix b)  //两矩阵相乘
{
    Matrix temp;
    memset(temp.a,,sizeof(temp.a));
    for(int i=;i<maxn;i++)
        for(int j=;j<maxn;j++)
            for(int k=;k<maxn;k++)
                temp.a[i][j]=(temp.a[i][j]+a.a[i][k]*b.a[k][j])%mod;
    return temp;
}

Matrix qpow(Matrix a,ll n)  //矩阵快速幂
{
    Matrix ans;
    memset(ans.a,,sizeof(ans.a));
    for(int i=;i<maxn;i++)
        ans.a[i][i]=; //化成单位矩阵
    while(n)
    {
        if(n&) ans=mul(ans,a);
        a=mul(a,a);
        n/=;
    }
    return ans;
}

int main()
{
    int t;
    scanf("%d",&t);
    Matrix A;
    A.a[][]=,A.a[][]=,A.a[][]=,A.a[][]=;
    A.a[][]=,A.a[][]=,A.a[][]=,A.a[][]=;
    A.a[][]=,A.a[][]=,A.a[][]=,A.a[][]=;
    A.a[][]=,A.a[][]=,A.a[][]=,A.a[][]=;
    while(t--)
    {
        ll n;
        scanf("%lld",&n);
        if(n<=)
        {
            printf("888\n");
            continue;
        }
        Matrix x=qpow(A,n-);
        ll ans=x.a[][]*+x.a[][]*+x.a[][]*+x.a[][]*;
        printf("%lld\n",ans%mod);
    }
    return ;
}