GDB调试32位汇编堆栈分析

GDB调试32位汇编堆栈分析

测试源代码

#include <stdio.h>

int g(int x){
	return x+5;
}

int f(int x){
	return g(x)+3;
}

int main(ing argv,char *argc[]){
	return f(7)+19;
}

• main函数汇编代码
  
  

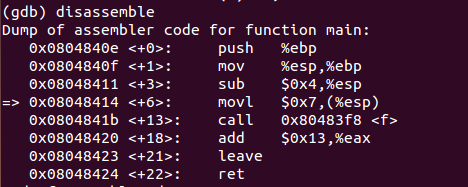
• g函数汇编代码
  
  

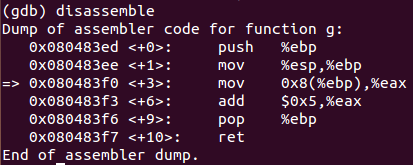
• f函数汇编代码
  
  

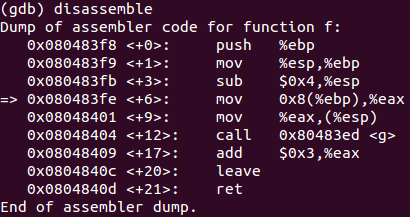
调试过程

• 在汇编调试中单步执行使用si，而display /i $pc该语句可以使得我们每一次单步执行时输出正在执行的语句，i r $xxx则可以输出对应的寄存器中的值，方便我们跟踪调试

• 根据代码，我们可以知道主函数只有return f(7)+19,在主函数中设下断点，可见当时%eip,%ebp,%esp,%eax的值（%eip为当前执行的指令的地址，%eax用于实参存储，计算，%ebp、%esp用于存储栈指针地址）
  
  

• 调用f函数，call指令将会将下一条指令的地址入栈，且此时esp将会减4
  
  

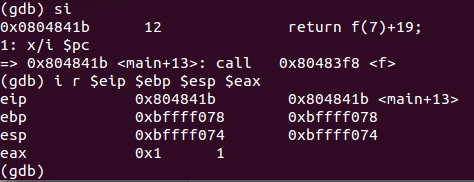
• 将eip中的值入栈，且此时esp已经发生了变化
  
  

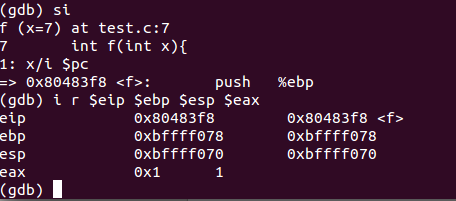
• 将上一个函数的基址入栈，当前%esp作为新基址
  
  

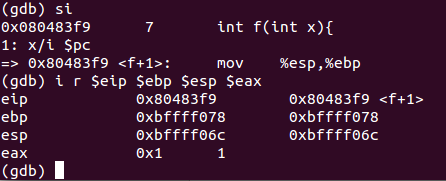
• %esp的值减4，将值传入%eax中，并不是太懂这几步到底有什么具体的作用，只知道最后的值实在%eax中进行计算的，大概这几步是为了最后计算做准备
  
  
  
  
  
  

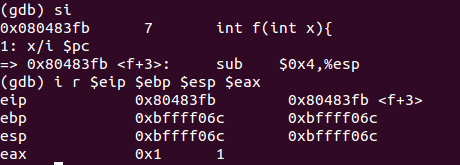
• call指令将下一条指令地址入栈，开始调用函数g（）
  
  

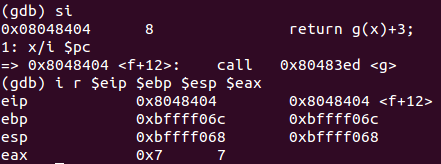
• 地址入栈
  
  

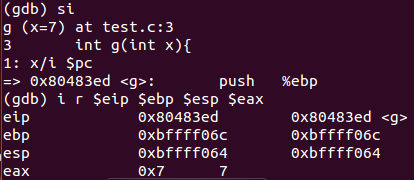
• 这几步和之前调用函数f()那几步作用应该是一样的，可能是传参用途（图值9、10）
  
  
  
  

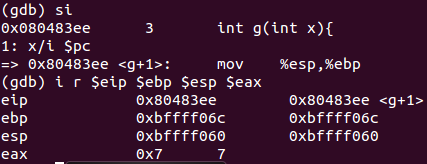
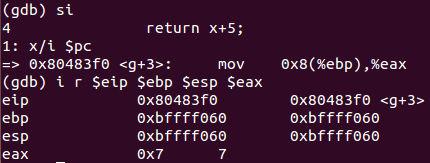
• 实参在%eax中进行计算
  
  

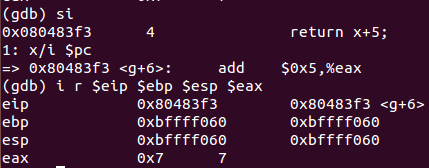
• 出栈，将地址弹到%ebp中
  
  

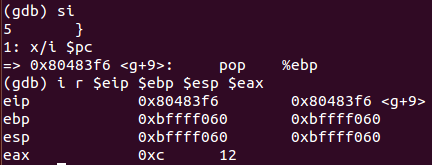
• ret指令将之前入栈的代码地址弹回%eip中，继续执行函数f()
  
  

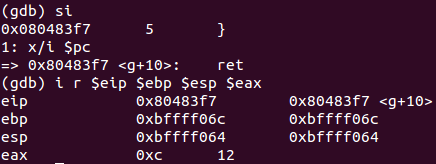
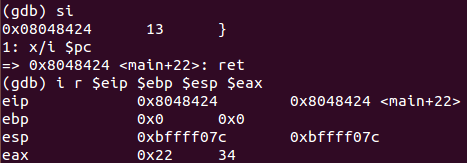
• 回到f函数中，进行实参的计算，然后出站，ret将代码地址弹回%eip，继续执行主函数main
  
  
  
  
  
  

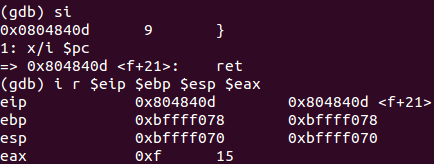
• 在主函数中完成计算，之后代码结束
  
  
  
  
  
  

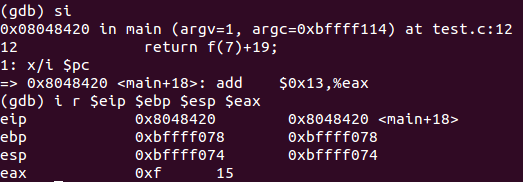
堆栈分析

指令	%esp	%ebp	%eip	%eax	堆栈
movl $0x7,(%esp)	0xbffff074	0xbffff078	0x8048414	0x1	0x0
call 0x80483f8	0xbffff074	0xbffff078	0x804841b	0x1	0x0
push %ebp	0xbffff070	0xbffff078	0x80483f8	0x1	0x8048420 0x0
mov %esp,%ebp	0xbffff06c	0xbffff078	0x80483f9	0x1	0xbffff078 0x8048420 0x0
sub $0x4,%esp	0xbffff06c	0xbffff06c	0x80483fb	0x1	0xbffff078 0x8048420 0x0
mov 0x8(%ebp),%eax	0xbffff068	0xbffff06c	0x80483fe	0x1	0xbffff078 0x8048420 0x0
mov %eax,(%esp)	0xbffff068	0xbffff06c	0x8048401	0x7	0xbffff078 0x8048420 0x0
call 0x80483ed	0xbffff068	0xbffff06c	0x8048404	0x7	0xbffff078 0x8048420 0x0
push %ebp	0xbffff064	0xbffff06c	0x8048404	0x7	0x8048409 0xbffff078 0x8048420 0x0
mov %esp,%ebp	0xbffff060	0xbffff06c	0x80483ee	0x7	0xbffff06c 0x8048409 0xbffff078 0x8048420 0x0
mov 0x8(%ebp),%eax	0xbffff060	0xbffff060	0x80483f0	0x7	0xbffff06c 0x8048409 0xbffff078 0x8048420 0x0
add $0x5,%eax	0xbffff060	0xbffff060	0x80483f3	0x7	0xbffff06c 0x8048409 0xbffff078 0x8048420 0x0
pop %ebp	0xbffff060	0xbffff060	0x80483f6	0x12	0xbffff06c 0x8048409 0xbffff078 0x8048420 0x0
ret	0xbffff064	0xbffff06c	0x80483f7	0x12	0x8048409 0xbffff078 0x8048420 0x0
add $0x3,%eax	0xbffff068	0xbffff06c	0x8048409	0x12	0xbffff078 0x8048420 0x0
leave	0xbffff068	0xbffff06c	0x804840c	0x15	0xbffff078 0x8048420 0x0
ret	0xbffff070	0xbffff078	0x804840d	0x15	0x8048420 0x0
add $0x13,%eax	0xbffff074	0xbffff078	0x8048420	0x15	0x0
leave	0xbffff074	0xbffff078	0x8048423	0x22	0x0
ret	0xbffff07c	0x0	0x8048424	0x22	0x0