数值分析之QR因子分解篇

在数值线性代数中，QR因子分解的思想比其他所有算法的思想更为重要[1]。

                                      --Lloyd N. Trefethen & David Bau, lll

在给出QR因子分解定理之前，先回顾两个知识点，一是正交矩阵（它的重要性在数值线性代数中似乎怎么强调都不过分），二是线性代数中的 Gram-Schmidt 正交化算法，这个算法是把一组线性无关的向量组alpha_1, ... ,alpha_n 转化为相互正交的向量组 q_1, ... ,q_n的方法，且有下列表达形式

q_k = a1*alpha_1+...+ak*alpha_k, k=1,...n

令A=[alpha_1, ... ,alpha_n], Q=[q_1, ... ,q_n], 则上式可以写成 Q = A*T， 其中T是一个上三角形矩阵。假设 A 是满秩的，则 T 具有逆矩阵，不妨记成R，在等式两边分别右乘矩阵R， 则可以得到A=QR。

针对一般矩阵，则有下列的 QR 因子分解定理：对于任意m*n维的实矩阵 A（不妨假设m>=n）,有相应的QR因子分解，即A=QR, 其中 Q 是具有正交列的m*m矩阵，R 是m*n的上三角矩阵，如图1.(a) 所示[1]。

         

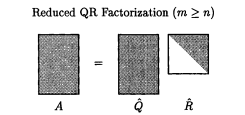
图1.(a)   完全 QR 因子分解                                图1.(b) 约化 QR 因子分解

如果将矩阵R的零行以及矩阵Q中不起作用的列去掉的话，则A=Q1R1，这里 Q1 具有列正交的m*n维矩阵，R1 是n*n的上三角矩阵，这种形式称为约化QR因子分解，如图1.(b) 所示，相应地，图1.(a)的分解形式称为完全QR因子分解。

既然矩阵有QR分解，那么一个自然的问题是给定一个具体的矩阵，如何求它的QR因子分解呢？实际上，从理论的角度来看，Gram-Schmidt正交化给出了一种数值实现的方法。不过，由于舍入误差的影响，该方法会在计算过程中损失正交性，即理论上求得的向量之间是相互正交的，但是数值求得的向量的正交性很差。因此，在求解QR因子分解中，传统的Gram-Schmidt正交化方法基本不用，而改用修正的Gram-Schmidt正交化方法。后者和前者相比，得到的向量的正交性更好，后者可以看成是一系列正交投影算子的作用，所谓 P 是一个正交投影算子，即它满足P*P=P（投影算子）以及P'=P。做个不恰当的类比，把向量之间的正交性看成是总体误差的话，前者只在最后一步进行了误差校正，而后者在每一步都进行误差校正，自然地，经过这样的处理，后者的误差显然比前者小。

观察 QR 因子分解，不管是传统还是修正的Gram-Schmidt正交化过程，它们通过对矩阵施行三角化（右乘上三角阵），来依次求出 Q 的每一列，在[2]中称作三角形对角化。另一种实现的方式是，通过构造一系列的正交矩阵（正交矩阵的乘积依旧是正交矩阵），来依次求出 R 的每一列（由于正交矩阵的转置即为它的逆，所以相应的Q也很容易求得），这种方法称为对角三角形化，如图2所示：

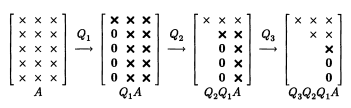
图2.  对角三角形化QR因子分解

下面的问题就是 Q 如何构造呢？点解，通过Householder变换或者Givens变换。先说Householder变换，参见图3，它将一个向量变换到只有前面数个坐标值非零，而后面的坐标值均为零的向量（参见图2，将A通过Q1变换后，A的第一列向量发生了改变）v，那么此时 Householder 变换为 Q1= I-2(vv')/(v'v)，其中v=-sign(x1)||x||e1，x是A的第一列，x1是向量x的第一个元素值，e1是第一个元素为1的单位向量(注1)。由于矩阵(vv')/(v'v)的秩为1，所以该变换也被称为单位阵的秩1修正。至于 Q2 以及 Q3 的构造，以 Q2 为例，考虑下列分块矩阵Q2=diag(I1, I2-2(v1v1')/(v1'v1))，其中v1是 Q1A 的第二列向量去掉第一个元素剩下的向量经过转换得到的，容易验证 Q2Q1A 就是图2中的结果。Givens 变换是一个旋转变换，每次将矩阵中的一个元素修改为0，与 Householder 变换相对应，它是单位矩阵的秩2修正。                            

图3. Householder变化示意图

总结一下，实现矩阵QR分解的方法有三角形对角化（修正的Gram-Schmidt算法，简称MGS）以及对角三角形化（Householder三角形化）。从数值结果的精度来看，尤其是正交矩阵之间的正交性来分析，后者比前者更好一些（注2），而Givens三角形化和Householder三角形化的结果相似[2]。但是，MGS可以根据需要在中间的某一步进行终止，而Householder三角形化却不具备这一特点。

拉拉杂杂说了这么多，有一个问题却没有提及，那就是 QR 方法有什么用途呢？点解。矩阵的特征值问题（除了使用QR算法外，还使用了逆迭代以及位移技术，因此QR算法被称为最复杂的算法），最小二乘法[3]以及多项式求根问题[4]中都有它的身影，而高斯消去法中涉及到的变换矩阵的某些性质在 MGS 中也出现过。

相应的Matlab命令： qr

注1. 从数学推导的角度来看，v的符号可以取为sign(x1)，之所以取成负数的形式，原因是为了避免两个相近的数字相减的情形，而这种情形很容易造成数值结果精度的很大损失。

注2. 简略地说，Householder三角化得到的正交矩阵的正交性和机器精度成正比，而MGS的正交矩阵的正交性和机器精度与矩阵A的条件数的乘积成正比。

注3. 文中涉及到的图片均取自参考资料[1]。

参考文献：

[1] 数值线性代数 Chap7-11，L N. Trefethen，David Bau, lll 著，陆金甫，关治译，人民邮电出版社，2006年

[2] 应用数值线性代数，J W. Demmel 著，王国荣译，人民邮电出版社，2007年

[3] 矩阵计算（第三版），Gene H.Golub，Charles F.Van Loan 著，袁亚湘等译，人民邮电出版社，2011年

[4]矩阵计算六讲 Chap2，徐树方，钱江著，高等教育出版社，2011年

作者：caicailiu 出处：http://www.cnblogs.com/liuyc/  欢迎转载或分享，但请务必声明文章出处。