Weighted Quick Union

Weighted Quick Union即:

在Quick Union的基础上对结点加权(weighted),在parent[i]基础上增加一个size[i].

用来存储该结点(site)的所有子结点数目.(size[i] == number of sites in subtree rooted at i)

具体操作步骤:

仅仅在union() operation改变,在改变parent前,增加一个步骤:

比较两个结点的size,谁更轻谁就在下面,

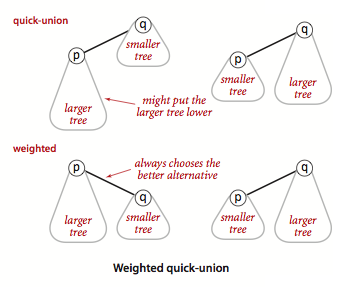
具体看代码:

 class WeightedQuickUnion():
     __count = int()     #number of components
     __parent = list()   #__parent[i] parent of i
     __size = list()     #size[i] number of sites in subtree rooted at i
     #Each site is initially in its own component
     def __init__(self,N):
         self.__count = N
         for i in range(0,self.__count):
             self.__parent.append(i)
             self.__size.append(1)
     #Return the component identifier for the component containing site
     def find(self,p):
         self.validate(p)
         while (p != self.__parent[p]):
             p = self.__parent[p]
         return p
     def connected(self,p,q):
         return self.find(p) == self.find(q)
     #Merges the component containig site p with
     #the component containing site q
     def union(self,p,q):
         rootP=self.find(p)
         rootQ=self.find(q)
         if (rootP == rootQ):
             return
         if (self.__size[rootP] < self.__size[rootQ]):
             self.__parent[rootP] = rootQ
             self.__size[rootQ] += self.__size[rootP]
         else:
             self.__parent[rootQ] = rootP
             self.__size[rootP] += self.__size[rootQ]
         self.__count-=1
     def validate(self, p):
         n = len(self.__parent)
         if (p < 0 or p >= n):
             raise ValueError("index", p, "is not between 0 and", (n - 1))
     def traversal(self):
         for i in self.__parent:
             print(i,end=' ')
 WQU = WeightedQuickUnion(8)
 WQU.union(0,1)
 WQU.union(2,1)
 WQU.union(2,4)
 WQU.union(3,7)
 print(WQU.connected(0,4))
 WQU.traversal()

实例同上一文Quick Find一样,

连接0-1-2-4 3-7,并调用connected()方法验证0-4是否连接

最后遍历

输出:

True
0 0 0 3 0 5 6 3 

根据输出可以反应出树形图:

　　　　　　0　　　　3　　5　　6

　 　　/　　|　　\　　|

　　1　　　2　　4     7

程序中:union()方法里,把size的比较分为两种情况,小于以及大于+等于.

union(0,1)的时候0是p,1是q,他们的size都是1,所以会执行

             self.__parent[rootQ] = rootP
             self.__size[rootP] += self.__size[rootQ]

也就是q(1)会成为p(0)的子节点.

union(3,7)同理.

其它情况由于size不同,会按照程序写的那样,把轻的作重的子节点