hihoCoder hiho一下 第一周 #1032 : 最长回文子串 (Manacher)

题意：给一个字符串，求最长回文子串的长度。

思路：

（1）暴力穷举。O(n^3)　-----绝对不行。

　　　　穷举所有可能的出现子串O(n^2)，再判断是否回文O(n)。就是O(n*n*n)了。

（2）记录位置。O(n^3)　-----绝对不行。

　　　　先扫一遍，记录每个字符在上一次出现的位置pos。每次考虑第i个字符，如果回文子串包括 i 的话，那么肯定在i的前面有一个跟第i个字符是一样的，利用之前记录的位置pos[i]可以找到与第i个相同的字符，如果i-pos[i]比之前发现的最长的子串max还短，那么不用比较了。如果更前面还有和第i个字符一样的，那么可以找到第pos[pos[i]]个，一定要找到区间比max还大的，才有比较的意义，除非前面已经没有相同字符的了。那么略过第i个，直奔下一个。记录位置需要O(n)，考虑每个字符需要O(n)，对其前面出现过的每个字符考虑O(n)，一旦考虑就需要比较是否回文O(n)，总的来说，后面3个是乘的关系O(n^3)。

 #include <iostream>
 #include <cstring>
 #include <vector>
 #include <stdio.h>

 using namespace std;
 const int N=;

 char str[N];
 char has[];
 char pos[N];

 bool isP(int j,int i)
 {
     while( j!=i && j!=--i)
     {
         if( str[j]!=str[i] )
             return false;
         j++;
     }
     return true;
 }

 int fin_ex(int max, int i)
 {
     int j=pos[i];
     while( i-j<=max && j>- )      //找到一个区间范围大于max的，开始算
         j=pos[j];
     return j;
 }

 int cal(int len)
 {
     int max=, j;
     for(int i=; i<len; i++)
     {
         j=fin_ex(max, i);      //找相同的，且大于max的
         while( j!=- && i-j>max )    //有相同
         {
             if(isP(j,i+)==true)
                 max=i-j+;
             else
                 j=fin_ex(max, j); //不是回文，继续找
         }
     }
     return max;
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     int t;
     cin>>t;
     getchar();
     while(t--)
     {
         gets(str);
         int len=strlen(str);
         for(int i=; i<; i++)    has[i]=-;      //初始化
         for(int i=; i<len; i++)                    //记录上一次出现的位置
         {
             pos[i]=has[str[i]];
             has[str[i]]=i;
         }

         cout<<cal(len)<<endl;
     }
     return ;
 }

TLE代码

（3）动态规划。时间O(n^2)，空间O(n^2)----这空间已经不行了。

　　　　不考虑了，这空间接受不了。

（4）中心扩展。时间O（n^2），空间O（0）。-----这时间已经不行了。

　　　　　　扫一遍每个字符需要O（n），对每个字符进行回文判断需要O（n）。总的就O（n^2）。

 #include <iostream>
 #include <cstring>
 #include <vector>
 #include <stdio.h>

 using namespace std;
 const int N=;
 int len;
 char str[N];

 int isP(int i)      //以i为中点的最长回文串的长度
 {
     int max1=;
     //奇数
     int tmp=max(i,len-i-);

     for(int j=; j<=tmp; j++)
     {
         if( str[i-j]==str[i+j] )
             max1+=;
         else
             break;
     }

     //偶数
     int max2=;
     tmp =max(i+, len-i-);
     for(int j=; j<tmp; j++)
     {
         if( str[i-j]==str[i+j+] )
             max2+=;
         else
             break;
     }
     return max1>max2? max1:max2;
 }

 int cal()
 {
     int max=, tmp;
     for(int i=; i<len-; i++)        //考虑以i为中心的回文串
     {
         if( (tmp=isP(i))>max )
             max=tmp;
     }
     return max;

 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     int t;
     cin>>t;
     while(t--)
     {
         scanf("%s",str);
         len=strlen(str);
         if(len==){cout<<""<<endl;continue;}
         cout<<cal()<<endl;
     }
     return ;
 }

TLE代码

（5）Manacher算法。时间O（n），空间O（n）。------完全OK！

　　　　主要目的就是要减少计算量，在”中心扩展“法的基础上，节省更多的计算量。下面介绍这种处理方法。

步骤：

　　1）首先要插入一些奇怪的字符。作用是，使得每种可能出现的子串的长度变成永远是奇数。如 abba 变成 #a#b#b#a#。假设串长为n，那么其实是加入了n+1个#号，使得串长总是2*n+1，这样就必定是奇数了。而且在用”中心扩展“法时仍然是奇数，考虑奇数子串#b#，偶数子串b#b，如果中间是#号，那么计算的就是偶数的子串了。置s[0]=‘￥’，随便一个特殊的字符，可以省去计算时的判断的左边界，比对到这个￥特殊符号，肯定没有任何一个是跟他匹配的，最长匹配过程自动就被终止了。而右边界有'\0'，自然也没有任何符号会跟他匹配。

　　2）接着需要记录下每个字符的关于最长子串的一些“信息”，不是长度，而是一个可以计算出长度的数字，其实是（纯长度+1），为什么要这么做？这其实是个边界。即下面提到的mx，在i到mx之间的字符都可以节省一些计算量。

　　（mx的对称点，id）和（id，mx）是对称的，即是回文的。能使得mx越靠右的字符位置就作为id，所以得及时凭借mx大小来更新id和mx。在（id，mx）中任意一个位置i都会和id左边对称的位置j有着一样的字符，那么以 i为中心的最小回文就跟以 j为中心的最大回文有关了，这也是减少计算量的突破口。假设用P[i]记录以位置i为中心的最长回文串的长度信息的话，有下面两种情况：

　　（1）以j为中心的最长回文串是（mx的对称点，id）里面的某一部分，则j-P[j]不会超过左边”mx的对称点“ 。那么这在P[id]管辖的范围内，有左右对称的原理，所以P[i]至少为P[j]吧，但是可能会更大，因为左边的是比较过的才求出P[j]，这P[i]还没比较过，所以长度可以从P[j]开始比对了。这样就节省了这P[j]次比较了。

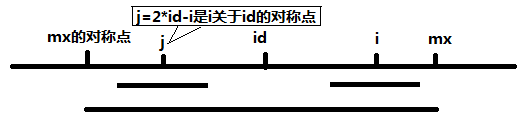
　　（2）P[j]超过了左边”mx的对称点“ 。超过了id的管辖范围了，多出的部分保证不了左右对称的原理了，但是在id管辖范围内的肯定是符合对称原理的，那么至少也可以减少一些计算量呐，减多少呢？就是”id管辖范围内“那个P[j]的长度了，做一些计算就可以得到这个长度是多少，但是肯定是小于P[j]的。

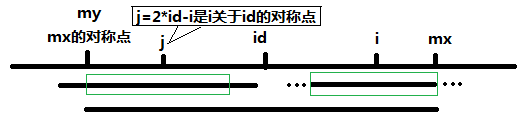
注：那如果i逐渐扫到mx之外了怎么办，i肯定找不到再关于id对称的j了。那就老老实实比较吧，继续用中心扩展。

 #include <iostream>
 #include <cstring>
 #include <vector>
 #include <stdio.h>
 using namespace std;
 const int N=;
 int len;            //原串长
 char str[N];        //接收原来的串
 char s[N*];        //做了插入处理的结果串
 int P[N*];         //保存关于长度的信息（回文长度的一半再加1）
 int cal()
 {
     int id=, mx=, max1=;
     P[]=;
     P[]=;
     for(int i=; s[i]!='\0'; i++)        //考虑以i为中心的回文串
     {
         P[i] =i>mx? : min( P[*id-i],mx-i);
         while(s[i+P[i]]==s[i-P[i]])     //在这比对
             P[i]++;
         if(i+P[i]>mx)       //更新id和mx的位置
         {
             id=i;
             mx=i+P[i];
         }
         if(P[i]->max1)     //更新最大值
             max1=P[i]-;
     }
     return max1;
 }

 int main()
 {
     freopen("input.txt", "r", stdin);
     int t;
     cin>>t;
     while(t--)
     {
         scanf("%s",str);
         len=strlen(str);
         memset(s,,sizeof(s));
         memset(P,,sizeof(P));

         //插入符号#
         s[]='$';
         s[]='#';
         int i=, j=;
         for(; i<len; i++)
         {
             s[j++]=str[i];
             s[j++]='#';
         }
         cout<<cal()<<endl;
     }
     return ;
 }

AC代码

用String实现了一发：

 #include <bits/stdc++.h>
 #define INF 0x7f7f7f7f
 #define pii pair<int,int>
 #define LL unsigned long long
 using namespace std;
 const int N=;

 int Manacher(string &str, int len)
 {
     //插上辅助字符#
     string tmp(len*+,'#');
     tmp[]='$';
     for(int i=; i<str.size(); i++)    tmp[i*+]=str[i];

     int ans=;
     int mx=, id=;
     vector<int> P(*len+,);

     for(int i=; i<tmp.size(); i++)
     {
         P[i]=( i>=mx? : min( P[*id-i], mx-i ));
         while( tmp[i-P[i]]==tmp[i+P[i]] )    P[i]++;    //匹配了就继续扩大P[i]

         if(mx<=i+P[i])//重要：更新位置
         {
             mx=i+P[i];
             id=i;
         }
         ans=max(ans, P[i]-); //这就是长度了，不信动手画。
     }
     return ans;
 }

 int main()
 {
     freopen("input.txt", "r", stdin);
     int t;
     string str;
     cin>>t;
     while(t--)
     {
         cin>>str;
         cout<<Manacher(str, str.size())<<endl;;
     }
     return ;
 }

AC代码