从零开始的全栈工程师——js篇2.1（js开篇）

JS开篇

一、js介绍

全称 javascript 但不是java 他是一门前台语言 而java是后台语言
js作者 布兰登·艾奇
前台语言：运行在客户端的
后台语言：跟数据库有关的

能干什么？    页面特效 开发网页游戏 后台开发等等

二、js和ECMAscript的关系

es不是语言 是js的标准 我们学习js得按es的标准学习

三、前端的三个层次

HTML  结构层

CSS  表现层

JS  行为层

四、js写在哪里

因为js和pho都是脚本语言 js写在script这个标签里 php写在<?php>标签里

当然作为一个合格的程序员最好把html css js三个文件分开

五、变量

变量：可以改变的量 并且区分大小写

变量的定义（声明）：var 加字母car a  我们声明了一个变量叫a

变量的用途：变量其实就是一个容器 起到临时存储数据的作用

通过等于号赋值（=）  var a=12；

六、js的语言输出

1.alert（）这是js中的一个方法 （弹出框）

2.console.log（）浏览器控制台输出 用于代码测试

3.document.write()在浏览器中写出

七、js的注释

1.单行注释 用两个 // 来进行单行注释

2.多行注释 /* 内容 */

八、常量 （不变的量）

1.汉字 数字 往往当做值使用 除了数字外要带引号“”  ( 双引号和单引号都可以)

红色的报错   说雅宁是一个变量 但这个变量没有被声明

undefined 说明有这个变量 但是没有赋值

2.变量的起名的规则 不能使用汉字 区分大小写 不能特殊符号开头除了_ $

_a（可以）    -a(减号不可以)        a3(字母后面可以带数字)    3a（而数字不可以写在字母前面）

带引号和不带引号

带引号的 是什么就输出什么——叫字符串（可以理解为“”里面的东西为内容）

变量不是 变量输出的是他后面的值 如果没有赋值 就是undefined

如下：

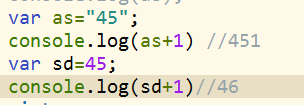
带引号的45是字符串 用+ 只是拼接 没带的是数字 +是四则运算

js的关键字  var function

九、js语言的四则运算

“+”号

纯数字之间就是加法
和字符串之间 +就是拼接

“-”号

纯数字之间就是减法
和字符串之间 -还是-

“*”号

纯数字之间就是乘法
和字符串之间 *还是*

“/”号
纯数字之间就是除以
和字符串之间 /还是/

减乘除 三者有隐式转换的能力 （隐式转换，在计算的过程中 将字符串强制转换成了数字）

%为取余

十、代码的执行顺序

1.代码执行顺序是从外往内从上往下 一个模块一个模块的执行

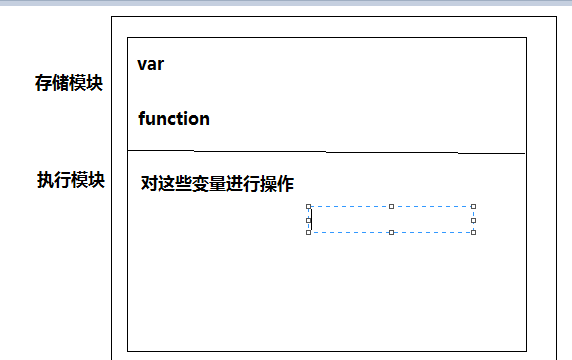
存储模块和执行模块
存储模块：var function 找到所有的js关键字
执行模块：对这些变量进行操作

2.变量提升：浏览器的功能

js执行前，浏览器会给一个全局作用域window

window分两个模块 一个存储模块 一个执行模块
存储模块 找到所有的var和function关键字 给这些变量添加内存地址
执行模块 代码从上到下执行 遇到变量就回去存储模块查找 有和没有
有，就看你赋值没有 赋值了就是后面的值 没有赋值就是undefined
如果没找到 结果就是xxx is not defined

如下：

十一、变量的值

暂时咱们只先学两个  一个字符串 一个数字   不管是字符串还是数字 后面的值统统成为数据

数据类型有：字符串 数字 数组 函数 布尔 对象 json null undefined

十二、运算

1.四则运算 + - * /在一起 先算*/后算+ - 有括号的先算括号里面的

2.逻辑运算 或（||）且（&&）非（|） 结果是布尔 true和false

3.比较运算 >大于 >=大于等于 <小于 <=小于等于 !取反 ==双等号

在js里  =是赋值 ==是等于 ===全等于（数据的类型和值 都一样）

==也有隐式转换的能力