平衡树学习笔记（5）-------SBT

SBT

上一篇：平衡树学习笔记（4）-------替罪羊树

所谓SBT，就是Size Balanced Tree

它的速度很快，完全碾爆Treap，Splay等平衡树，而且代码简洁易懂

尤其是插入节点多的时候，比其它树快多了（不考虑毒瘤红黑树）

尤其是它的平衡操作maintain，均摊\(O(1)\)!!!!

他maintain跟Splay差不多，都是依靠旋转来平衡

不过他可不想splay那样直接转到根，而是有条件的旋转

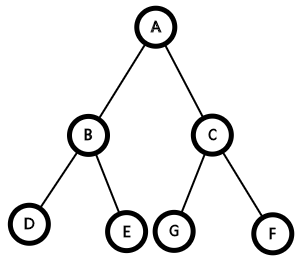
拿上图来说，SBT对于每个点，有两个平衡条件，假设说当前点是A，那么要满足以下两个条件，A才平衡

1、\(siz(B)\ge siz(G),siz(F)\)

2、\(siz(C)\ge siz(D),siz(E)\)

\(\color{#9900ff}{定义}\)

struct node {
	node *ch[2];
	int val, siz;
	node(int val = 0, int siz = 0): val(val), siz(siz) { ch[0] = ch[1] = NULL; }  //构造函数
	void upd() { siz = ch[0]->siz + ch[1]->siz + 1; }   //维护siz
	int rk() { return ch[0]->siz + 1; }       //获取当前排名
}*root, *null, pool[maxn], *tail, *st[maxn];  // 根，哨兵，内存池，当前指针，回收池

定义根Splay差不多，只是不用记录父亲

这里可以建立一个哨兵null，判断siz的时候比较好写

\(\color{#9900ff}{基本操作}\)

1、rotate

这个是旋转，跟Splay差不多

但是SBT是不用记录父亲的，所以要简单一点

这里有2个参数rotate(x,k)

意为把x向它的孩子k方向转

即为把x的另一个孩子!k转上来

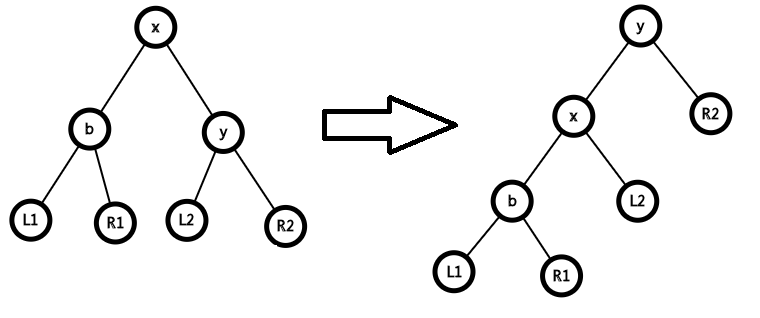
void rot(node *&x, int k) {  //注意这里要取地址，maintain的时候也要取地址，目的是让x维护的是位置，而不是特定的点
	node *w = x->ch[!k];   //w就是上图的L2，即旋转中特殊的那个点
	x->ch[!k] = w->ch[k], w->ch[k] = x, w->siz = x->siz;
	x->upd(), x = w;   //让x仍然维护原来的位置
}

2、maintain

这是SBT维护平衡的操作函数

它基于1.rotate进行各种旋转

虽然看起来复杂度有点高

其实均摊可以达到\(O(1)\)！（虽然我不会证）

维护平衡一定要考虑全面，一旦露了某个子树，可能就会被卡QWQ

首先，先声明一点，maintain只有插入才会用到

因为删除不会增加复杂度，其它操作，树的形态又没变

因此，用到maintain的唯有插入

插入怎么插呢？

我们采用的是递归插入（必须递归插入，因为沿途每个点siz一变大，就可能不平衡！）

沿途siz++

那么，很显然可以得到从它到根的一条链

由于沿途siz++，所以

途中的这些点都有可能需要平衡

maintain（x，k）代表平衡x，至于k，左右哪边重，k就是哪边

下面我们开始分情况讨论一下maintain操作

我们发现，俩条件是对称的！下面我们只讨论一个条件，另一个就是反过来而已

Case 1： siz(A) > siz(R)

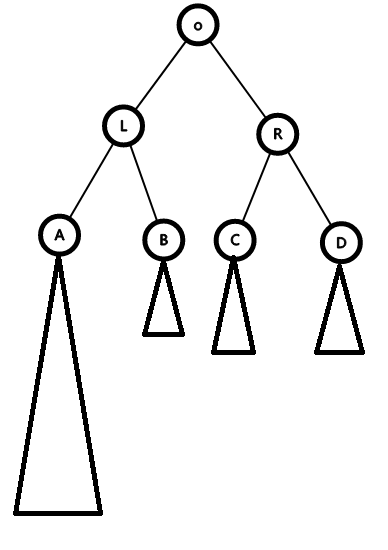
这时候我们把L转上来，就成了这样

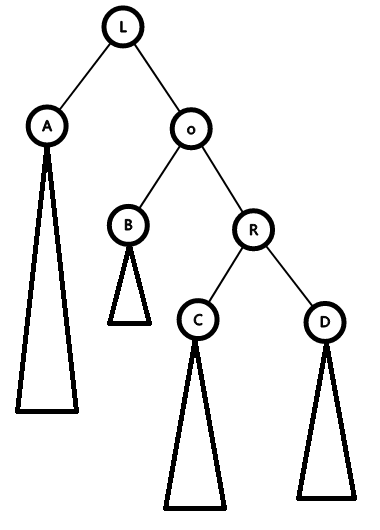
但是o可能还是不平衡，比如上图，右边偏重，所以我们要继续maintain

Case 2： siz(B) >siz(R)

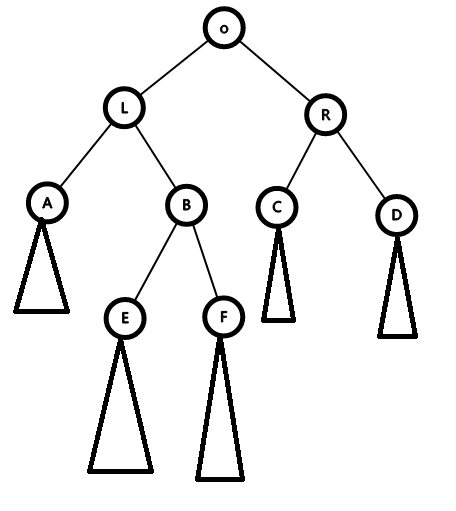
这时，我们把B直接转到o的位置上，即B左旋再右旋

然后，树就变成了这个样子

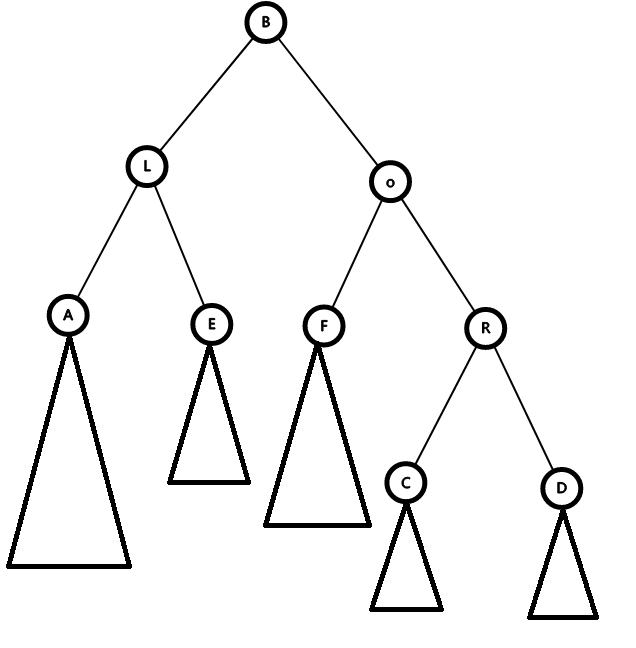
这时候会有好多地方不平衡qwq，但是可以发现，AEFR这些子树只是换了个位置，没有变，依然满足性质

因此我们调用两次maintain来平衡L和o

这个时候，除了B，其它所有点的子树都OK了，就剩下B了，它可能不满足1或2，所以再maintain(B)一下

代码实现的时候，可以记录一下哪边重，然后就可以写到一起，很简洁，好记

void maintain(node *&o, int k) {  //平衡o，哪边重，k就是哪边
	if(o->ch[k]->ch[k]->siz > o->ch[!k]->siz) rot(o, !k);  //情况1,
	else if(o->ch[k]->ch[!k]->siz > o->ch[!k]->siz) rot(o->ch[k], k), rot(o, !k); //情况2
	else return;
	maintain(o->ch[0], 0), maintain(o->ch[1], 1), maintain(o, 0), maintain(o, 1); //统一平衡，即使有些情况不涉及，反正递归下去也是直接return
}

\(e\color{#9900ff}{其它操作}\)

1、插入

关于插入，上面提了几句

总的来说就是从根出发，往孩子跳

这是一个递归的过程，必须递归，因为沿途回溯的时候要maintain，当然手动模拟递归也不拦你

void ins(node *&o, int val) {
	if(o == null) return (void)(o = newnode(val));  //到空节点，直接开新节点就行
	o->siz++;                                       //沿途siz++
	if(val <= o->val) ins(o->ch[0], val);           //找到插入位置
	else ins(o->ch[1], val);
	maintain(o, val > o->val);                      //每个点的子树进行平衡，在哪边插的，哪边可能就会变重，所以要平衡那一边
}

2、删除

因为它并没有Splay那样直接转到根这样的条件

它的旋转只是基于siz来的

所以，我们需要一些特别的方式

首先我们找到要删除的那个点，如果发现那个点并不是左右儿子都有，那就把那个儿子接上来就行了

否则，它一定存在左右儿子，也就是说它有后继，我们可以直接暴力找到它的后继，然后点权赋过来，改成在右边删除它的后继

见代码

void del(node *&o, int val) {
    //只要没找到，就递归删
	if(o->val != val) return (void)(del(o->ch[val > o->val], val), o->upd());
    //删除同理，沿途siz--
	o->siz--;
    //定义一个临时变量p为当前节点
	node *p = o;
    //如果x有一个孩子是空的，那么就简单了
    //把他不空的孩子接上来代替他的位置
    //显然不会影响平衡树的性质
    //这时只需把p删了即可
	if(o->ch[0] == null) o = o->ch[1], st[++top] = p;
	else if(o->ch[1] == null) o = o->ch[0], st[++top] = p;
	else {
        //这就是没有空孩子的情况
		p = o->ch[1];
		while(p->ch[0] != null) p = p->ch[0];
        //让p为o的后继（暴力找）
        //除了siz之外，二者全部交换
        //虽然o的值变成了p的
        //但是p的值没有改变！！！
        //因此，我们相当于已经用p代替了o
        //而且，因为p是o的后继，所以接上一定是满足平衡树性质的！
        //所以，我们的目标就只有一个了，那就是删掉p
        //而p作为后继，一定在o的右子树内
        //而且通过刚刚找后继的方式来看，它的左儿子一定是空的
        //所以当前位置的递归最多只会进入一次
        //这样也保证了复杂度！
		o->val = p->val, del(o->ch[1], p->val);
	}
}

上面一定要理解透彻

3、查询数x的排名

剩下的就差不多了qwq

int rnk(int val) {
	node *o = root; int rank = 0;
	while(o != null) {
		if(o->val < val) rank += o->rk(), o = o->ch[1];
		else o = o->ch[0];
	}
	return rank + 1;
}

4、查询第k大的数

int kth(int k) {
	node *o = root;
	while(o->rk() != k) {
		if(k > o->rk()) k -= o->rk(), o = o->ch[1];
		else o = o->ch[0];
	}
	return o->val;
}

5,6、前驱，后继

跟Splay的一毛一样qwq

毕竟都是平衡树，多少有点通性

int pre(int val) {
	node *o = root, *lst = null;
	while(o != null) {
		if(o->val < val) lst = o, o = o->ch[1];
		else o = o->ch[0];
	}
	return lst->val;
}
int nxt(int val) {
	node *o = root, *lst = null;
	while(o != null) {
		if(o->val > val) lst = o, o = o->ch[0];
		else o = o->ch[1];
	}
	return lst->val;
}

最后，放下完整代码

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 1e5 + 10;
struct SBT {
	protected:
		struct node {
			node *ch[2];
			int val, siz;
			node(int val = 0, int siz = 0): val(val), siz(siz) { ch[0] = ch[1] = NULL; }
			void upd() { siz = ch[0]->siz + ch[1]->siz + 1; }
			int rk() { return ch[0]->siz + 1; }
		}*root, *null, pool[maxn], *tail, *st[maxn];
		int top;
		node *newnode(int val) {
			node *o = new(top? st[top--] : tail++) node(val, 1);
			return o->ch[0] = o->ch[1] = null, o;
		}
		void rot(node *&x, int k) {
			node *w = x->ch[!k];
			x->ch[!k] = w->ch[k], w->ch[k] = x, w->siz = x->siz;
			x->upd(), x = w;
		}
		void maintain(node *&o, int k) {
			if(o->ch[k]->ch[k]->siz > o->ch[!k]->siz) rot(o, !k);
			else if(o->ch[k]->ch[!k]->siz > o->ch[!k]->siz) rot(o->ch[k], k), rot(o, !k);
			else return;
			maintain(o->ch[0], 0), maintain(o->ch[1], 1), maintain(o, 0), maintain(o, 1);
		}
		void ins(node *&o, int val) {
			if(o == null) return (void)(o = newnode(val));
			o->siz++;
			if(val <= o->val) ins(o->ch[0], val);
			else ins(o->ch[1], val);
			maintain(o, val > o->val);
		}

		void del(node *&o, int val) {
			if(o->val != val) return (void)(del(o->ch[val > o->val], val), o->upd());
			o->siz--;
			node *p = o;
			if(o->ch[0] == null) o = o->ch[1], st[++top] = p;
			else if(o->ch[1] == null) o = o->ch[0], st[++top] = p;
			else {
				p = o->ch[1];
				while(p->ch[0] != null) p = p->ch[0];
				o->val = p->val, del(o->ch[1], p->val);
			}
		}
	public:
		SBT() {
			tail = pool; top = 0;
			root = null = new node();
			null->ch[0] = null->ch[1] = null;
		}
		void ins(int val) { ins(root, val); }
		void del(int val) { del(root, val); }
		int rnk(int val) {
			node *o = root; int rank = 0;
			while(o != null) {
				if(o->val < val) rank += o->rk(), o = o->ch[1];
				else o = o->ch[0];
			}
			return rank + 1;
		}
		int kth(int k) {
			node *o = root;
			while(o->rk() != k) {
				if(k > o->rk()) k -= o->rk(), o = o->ch[1];
				else o = o->ch[0];
			}
			return o->val;
		}
		int pre(int val) {
			node *o = root, *lst = null;
			while(o != null) {
				if(o->val < val) lst = o, o = o->ch[1];
				else o = o->ch[0];
			}
			return lst->val;
		}
		int nxt(int val) {
			node *o = root, *lst = null;
			while(o != null) {
				if(o->val > val) lst = o, o = o->ch[0];
				else o = o->ch[1];
			}
			return lst->val;
		}
}s;
int main() {
	for(int T = in(); T --> 0;) {
		int p = in();
		if(p == 1) s.ins(in());
		if(p == 2) s.del(in());
		if(p == 3) printf("%d\n", s.rnk(in()));
		if(p == 4) printf("%d\n", s.kth(in()));
		if(p == 5) printf("%d\n", s.pre(in()));
		if(p == 6) printf("%d\n", s.nxt(in()));
	}
	return 0;
}

下一篇：平衡树学习笔记（6）-------RBT